Đáp án cần chọn là: A

Với n = 0 ta có: $S_0=3$ chia hết cho 3, ta chứng minh $S_n=n^3+3n^2+5n+3$ chia hết cho 3 với mọi số tự nhiên n.

Giả sử mệnh đề trên đúng đến $n=k,$ tức là $S_k=k^3+3k^2+5k+3$ chia hết cho 3, ta chứng minh mệnh đề trên đúng đến $n=k+1$, tức là $S_{k+1}$ cũng chia hết cho 3.

Ta có:

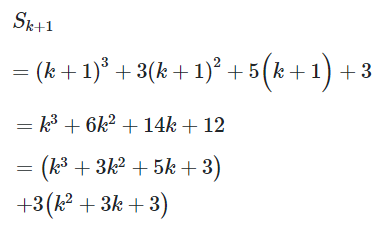
Có:  $S_k=k^3+3k^2+5k+3$ chia hết cho 3 theo giả thiết quy nạp,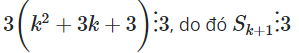 

Vậy $S_n⋮3$ với mọi số tự nhiên n.

Đáp án cần chọn là: D

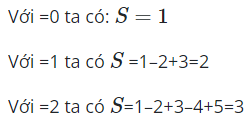
Dự đoán S = n+1$\left(*\right)$ ta sẽ chứng minh $\left(*\right)$đúng bằng quy nạp.

Với n = 0 đương nhiên $\left(*\right)$ đúng.

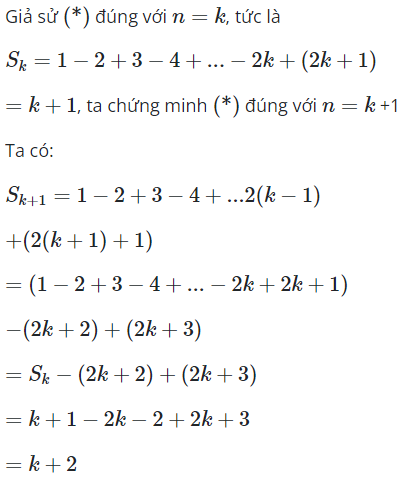
Vậy  đúng với mọi số tự nhiên n, tức là S = n+1.

Với =1 ta có: S =1.2=2, do đó đáp án A, C sai.

Ta chứng minh  đúng với mọi số nguyên dương .

, ta chứng minh (∗) đúng đến $n=k+1$, tức là cần chứng minh

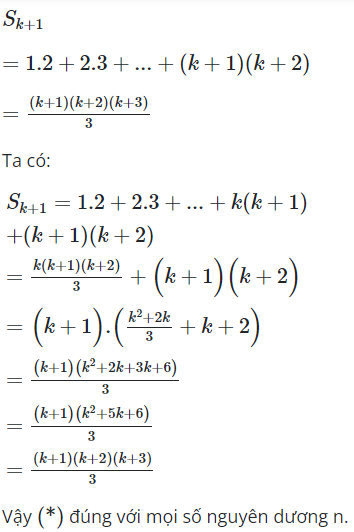
Đáp án cần chọn là: B

Quan sát lời giải trên ta thấy:

Học sinh thực hiện thiếu bước 1: Kiểm tra $n=1$ thì $8^1$+1=9 không chia hết cho 7 nên mệnh đề đó sai.

Đáp án cần chọn là: D

Bằng quy nạp toán học ta chứng minh được  $7^n$+ 5  chia hết cho 6.

Thật vậy, với n = 1 ta có: $7^1+5=12⋮6$

Giả sử mệnh đề đúng với n = k , nghĩa là  $7^k+5$ chia hết cho 6, ta chứng minh mệnh đề cũng đúng với , nghĩa là phải chứng minh $7^{k+1}+5$ chia hết cho 6.

Ta có: $7^{k+1}+5=7\left(7^k+5\right)-30$

Theo giả thiết quy nạp ta có $7^k$+5 chia hết cho 6, và 30 chia hết cho 6 nên 

$7\left(7^k+5\right)-30$ cũng chia hết cho 6.

Do đó mệnh đề đúng với $n=k+1$

Vậy $7^n$ + 5  chi hết cho 6 với mọi $n\in N^{*}$

Mọi số chia hết cho 6 đều chia hết cho 2 và chia hết cho 3.

Do đó cả 3 mệnh đề đều đúng.

Đáp án cần chọn là: A

Nếu ta giả sử mệnh đề đúng với $n=k$ thì ta cần chứng minh mệnh đề đúng với $n=k+1$ 

Đáp án cần chọn là: C

Đối với bài toán chứng minh $P\left(n\right)$ đúng với mọi $n\ge p$ với p là số tự nhiên cho trước thì:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=p$

- Bước 2: Với $k\ge p$ là một số nguyên dương tùy ý, giả sử $P\left(n\right)$ đúng với $n=k$, chứng minh $P\left(n\right)$ cũng đúng khi $n=k+1$.

Từ đó ta thấy, ở bước đầu tiên ta cần chứng minh mệnh đề đúng với $n=p$ chứ không phải $n=1$.

Đáp án cần chọn là: D

Ở bước 2 ta cần giả sử mệnh đề đúng với $n=k$ với $k\ge p$.

Đáp án cần chọn là: B

Đối với bài toán chứng minh $P\left(n\right)$ đúng với mọi $n\ge p$ với p là số tự nhiên cho trước thì:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=p$.

- Bước 2: Với là một số nguyên dương tùy ý, giả sử đúng với , chứng minh cũng đúng khi $n=k+1$.

Từ lý thuyết trên ta thấy cả hai bước trên đều đúng.

Đáp án cần chọn là: C

Phương pháp quy nạp toán học:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=1$.

- Bước 2: Với k là một số nguyên dương tùy ý, giả sử $P\left(n\right)$ đúng với $n=k$, chứng minh $P\left(n\right)$ cũng đúng khi $n=k+1$.

Do đó ta thấy, ở bước 2, nếu ta giả sử mệnh đề đúng với thì ta cần chứng minh mệnh đề đúng với 1

Đáp án cần chọn là: B

Đáp án A: sai vì Q là tập con thực sự của N* nên tồn tại số nguyên dương không thuộc Q.

Đáp án B: đúng vì theo lý thuyết của phương pháp quy nạp toán học.

Đáp án C: sai vì theo giả thiết b thì phải là số tự nhiên lớn hơn k thuộc Q.

Đáp án D: sai vì số nguyên âm không thuộc Q.

Đáp án cần chọn là: B

Dễ thấy p = 2 thì bất đẳng thức $2^p>2p+1$ là sai nên loại ngay phương án D.

Xét với p = 3 ta thấy $2^p>2p+1$ là bất đẳng thức đúng. Bằng phương pháp quy nạp toán học chúng ta chứng minh được rằng $2^n>2n+1$ với mọi $n\ge 3$

Vậy p =  là số nguyên dương nhỏ nhất cần tìm.

Đáp án cần chọn là: B

Gọi $S_n=2+5+8+\mathrm{...}+(3n-1)$

Với n = 1 ta có: $S_1=2$ , ta loại được các đáp án B, C và D.

Ta chứng minh

 $S_n=2+5+8+\mathrm{...}+(3n-1)$

$=\frac{n(3n+1)}{2}(*)$ đúng với mọi số nguyên dương n bằng phương pháp quy nạp toán học.

Giả sử $\left(*\right)$ đúng đến $n=k(k\ge 1)$ tức là 

$S_k=2+5+8+\mathrm{...}+(3k-1)$

$=\frac{k(3k+1)}{2}$

Ta cần chứng minh (*) đúng đến $n=k+1$, tức là cần chứng minh

$S_{k+\text{}1}=2+5+\mathrm{...}+\left(3\right(k+1)-1)$

$=\frac{(k+\text{}1).\left(3\right(k+1)+1)}{2}$

Thật vậy ta có:

$\begin{array}{l}{S}_{k+\text{}1}=2+5+\mathrm{...}+\left(3\right(k+1)-1)\\ =\frac{k(3k+1)}{2}+\text{}\left(\text{}3\right(k+1)-1)\\ =\frac{k(3k+1)}{2}+(3k+2)\\ =\frac{3k^2+\text{}k+\text{}6k+\text{}4}{2}\\ =\frac{3k^2+\text{}7k+\text{}4}{2}\\ =\frac{(k+1)(3k+4)}{2}\end{array}$

Do đó (*) đúng đến $n=k+1$.

Vậy $S_n=2+5+8+\mathrm{...}+(3n-1)$

$=\frac{n(3n+1)}{2}$  đúng với mọi số nguyên dương n.

Đáp án cần chọn là: A

Bằng cách phân tích số hạng đại diện, ta có: 

$1-\frac{1}{k^2}=\frac{k-1}{k}.\frac{k+1}{k}$

Suy ra 

$\begin{array}{l}\left(1-\frac{1}{4}\right)\left(1-\frac{1}{9}\right)\mathrm{...}\left(1-\frac{1}{n^2}\right)\\ =\frac{1}{2}.\frac{3}{2}.\frac{2}{3}.\frac{4}{3}\mathrm{...}\frac{n-1}{n}.\frac{n+1}{n}\end{array}$

$=\frac{n+1}{2n}=\frac{2n+2}{4n}$

Đối chiếu với đẳng thức đã cho ta có: $a=2,b=4$

Suy ra $P=a^2+b^2=20$

Đáp án cần chọn là: C

Với $n=1$ ta có $\frac{a+b}{2}=\frac{a+b}{2}$, do đó loại đáp án A.

Với n = 2, chọn bất kì a = 1, b = 2 ta có:

Đáp án C sai.

Ta chứng minh đáp án B đúng với mọi $a\ge 0,b\ge 0,n\in N*$ bằng phương pháp quy nạp.

Với n =1 mệnh đề đúng.

Giả sử mệnh đề đúng đến $n=k(k\ge 1)$

$\iff \frac{a^k+b^k}{2}\ge {\left(\frac{a+b}{2}\right)}^k\left(1\right)$

Ta phải chứng minh $\frac{a^{k+1}+b^{k+1}}{2}\ge {\left(\frac{a+b}{2}\right)}^{k+1}$

 Thật vậy, ta nhân 2 vế của (1) với $\frac{a+b}{2}>0$ ta có:

$\begin{array}{l}\frac{a^k+b^k}{2}.\frac{a+b}{2}\ge {\left(\frac{a+b}{2}\right)}^k.\frac{a+b}{2}\\ \iff \frac{a^{k+1}+a^{k}b+a{b}^k+b^{k+1}}{4}\ge {\left(\frac{a+b}{2}\right)}^{k+1}\left(2\right)\end{array}$

Do $a\ge 0,b\ge 0$. Nếu $a\ge b\ge 0\Rightarrow (a^k-b^k)(a-b)\ge 0$, nếu

$\begin{array}{l}0\le a\le b\Rightarrow \left(a^k-b^k\right)(a-b)\ge 0\\ \Rightarrow \left(a^k-b^k\right)(a-b)\ge 0\forall a\ge 0,b\ge 0\end{array}$

$\Rightarrow a^{k+1}+b^{k+1}\ge a^{k}b+a{b}^k$

$\Rightarrow \frac{a^{k+1}+a^{k}b+a{b}^k+b^{k+1}}{4}$

$\le \frac{a^{k+1}+a^{k+1}+b^{k+1}+b^{k+1}}{4}$

$=\frac{a^{k+1}+b^{k+1}}{2}$

Từ (2) suy ra $\frac{a^{k+1}+b^{k+1}}{2}\ge {\left(\frac{a+b}{2}\right)}^{k+1}$, do đó mệnh đề đúng đến $n=k+1$

Vậy mệnh đề đúng với mọi $n,a,b$ thỏa mãn điều kiện bài toán.

Đáp án cần chọn là: B

Cách 1: (trắc nghiệm) Kiểm tra tính đúng – sai của từng phương án đến khi tìm được phương án đúng thông qua một số giá trị cụ thể của nn.

+ Với $n=1$ thì $S=1^2=1$ (loại được các phương án B và D);

+ Với $n=2$ thì $S=1^2+2^2=5$ (loại được phương án A).

Vậy phương án đúng là C.

Cách 2. Chứng minh bằng phương pháp quy nạp

Đáp án cần chọn là: C

Với $n=2$ ta có: $3^2=9>3.2+2$

Ta chứng minh đáp án C đúng bằng phương pháp quy nạp toán học.

Bất đẳng thức đúng với $n=2$, giả sử bất đẳng thức đúng đến $n=k(k\ge 2)$, tức là $3^k>3k+2$.

Ta chứng minh bất đẳng thức đúng đến $n=k+1$, tức là cần phải chứng minh 

$3^{k+1}>3(k+1)+2=3k+5$

Ta có: 

$3^{k+1}={3.3}^k>3(3k+2)$

$=9k+6>3k+5$

Vậy bất đằng thức đúng với mọi số tự nhiên $n\ge 2$

Đáp án cần chọn là: C

Ta dùng phương pháp quy nạp để chứng minh với mọi số nguyên dương n thì:

 $1.4+2.7+\cdot \cdot \cdot +n\left(3n+1\right)$

$=n{\left(n+1\right)}^2$ (1)

Với n = 1: Vế trái của (1)  = 1. 4 = 4.

 Vế phải của (1) $=1{(1+1)}^2=4$.

 Suy ra Vế trái của (1) = Vế phải của (1).  Vậy (1) đúng với n = 1.

Giả sử (1) đúng với n = k . Có nghĩa là ta có:

$1.4+2.7+\cdot \cdot \cdot +k\left(3k+1\right)$

$=k{\left(k+1\right)}^2\left(2\right)$

Ta phải chứng minh (1) đúng với n = k + 1  . Có nghĩa ta phải chứng minh:

$1.4+2.7+\cdot \cdot \cdot +k\left(3k+1\right)$

$+\left(k+1\right)\left(3k+4\right)$

$=\left(k+1\right){\left(k+2\right)}^2$

Thật vậy

 $\underset{=k{\left(k+1\right)}^2}{\underbrace{1.4+2.7+\cdot \cdot \cdot +k\left(3k+1\right)}}$

$+\left(k+1\right)\left(3k+4\right)$

$=k{\left(k+1\right)}^2+\left(k+1\right)\left(3k+4\right)$

$=(k+\text{}1).\text{[\hspace{0.17em}}k.(k+1)+\text{}3k+\text{}4\text{]\hspace{0.17em}}$

  $=(k+\text{}1).(k^2+4k+4)$                                                                  

$=\left(k+1\right){\left(k+2\right)}^2$ (đpcm).

Vậy (1) đúng khi n =  k + 1 . Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Chọn  A

Đặt $u_n=n^3+\text{}3n^2+5n$

Ta có $u_1=1^3+{3.1}^2+5.1=9$ chia hết cho 3.

Giả sử $u_k=k^3+\text{}3k^2+5k$ chia hết cho 3.

Ta cần chứng minh

$$\begin{gathered} u_{k+1}={\left(k+1\right)}^3+3{\left(k+1\right)}^2 \\ +5\left(k+1\right) \end{gathered}$$ chia hết cho 3.

Thật vậy, ta có:
 $u_{k+1}$

$=k^3+3k^2+3k+1+3k^2+6k+3$

$+5k+5$

$=k^3+\text{\hspace{0.17em}\hspace{0.17em}}6k^2+\text{\hspace{0.17em}}14k+\text{}9$

$=(k^3+\text{}3k{}_2+\text{}5k)$

$+\text{\hspace{0.17em}\hspace{0.17em}}(3k^2\text{}+\text{\hspace{0.17em}\hspace{0.17em}}9k+\text{\hspace{0.17em}}9)$

$=u_k+3\left(k^2+3k+3\right)$.

 Vì $u_k$ và $3\left(k^2+3k+3\right)$ đều chia hết cho 3, nên $u_{k+\text{}1}$ cũng chia hết cho 3.

Vậy với mọi số nguyên dương n thì $u_n$ chia hết cho 3.

Kiểm tra tính đúng – sai của bất đẳng thức với các trường hợp = 1,2,3,4, ta dự đoán được $2^{n+1}>n^2+3n$, với $n\ge$4. Ta chứng minh bất đẳng thức này bằng phương pháp quy nạp toán học. Thật vây:

- Bước 1: Với $n=4$ thì vế trái bằng $2^{4+1}=2^5=32$, còn vế phải bằng $4^2+3.4=28$

Do 32>28 nên bất đẳng thức đúng với $n=4$

- Bước 2: Giả sử đẳng thức đúng với $n=k\ge 4$, nghĩa là $2^{k+1}>k^2+3k$

Ta phải chứng minh bất đẳng thức cũng đúng với $n=k+1$, tức là phải chứng minh $2^{(k+1)+1}>{(k+1)}^2+3(k+1)$ hay $2^{k+2}>k^2+5k+4$ 

Thật vậy, theo giả thiết quy nạp ta có $2{}_{k+1}>k^2+3k$

Suy ra ${2.2}^{k+1}>2(k^2+3k)$ hay $2^{k+2}>2k^2+6k$

Mặt khác:

$2k^2+6k-(k^2+5k+4)$

$=k^2+k-4\ge 4^2+4-4=16$ với mọi $k\ge 4$

Do đó $2^{k+2}>2(k^2+3k)>k^2+5k+4$ hay bất đẳng thức đúng với $n=k+1$.

Suy ra bất đẳng thức được chứng minh.

Vậy phương án đúng là D.

Đáp án cần chọn là: D

Cách 1:

Bằng phương pháp quy nạp toán học, ta sẽ chứng minh được 

$S_n=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\mathrm{...}+\frac{1}{n(n+1)}$

= $\frac{n}{n+1}(*)$

Thật vậy, với $n=1$ ta có $S_1=\frac{1}{1.2}=\frac{1}{2}=\frac{1}{1+1}$

Giả sử $(*)$ đúng đến $n=k(k\ge 1)$ khi đó ta có:

$S_k=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\mathrm{...}+\frac{1}{k(k+1)}$$=\frac{k}{k+1}$, ta chứng minh (*) đúng đến $n=k+1$, tức là cần chứng minh

$S_k=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\mathrm{...}+\frac{1}{k(k+1)}$

$=\frac{k+1}{k+2}$

Ta có:

$S_{k+1}$

$=\frac{1}{1.2}+\frac{1}{2.3}+\mathrm{...}+\frac{1}{k(k+1)}+\frac{1}{(k+1)(k+2)}$

$=\frac{k}{k+1}+\frac{1}{(k+1)(k+2)}$

$=\frac{k(k+2)+1}{(k+1)(k+2)}$

$=\frac{k^2+2k+1}{(k+1)(k+2)}$

$=\frac{{(k+1)}^2}{(k+1)(k+2)}$

$=\frac{k+1}{k+2}$

Vậy  đúng với mọi số nguyên dương .

Đáp án cần chọn là: B

Cách 1: Rút gọn biểu thức $S_n$ dựa vào việc phân tích phần tử đại diện.

Với mọi số nguyên dương , ta có $\frac{1}{(2k-1)(2k+1)}$$=\frac{1}{2}\left(\frac{1}{2k-1}-\frac{1}{2k+1}\right)$

Do đó:

$S_n$

$=\frac{1}{2}\left(1-\frac{1}{3}+\mathrm{...}+\frac{1}{2n-1}-\frac{1}{2n+1}\right)$

$=\frac{1}{2}\left(1-\frac{1}{2n+1}\right)=\frac{n}{2n+1}$

Vậy phương án đúng là phương án C.

Cách 2. Dùng phương pháp quy nạp chứng minh C đúng.

Đáp án cần chọn là: C

Cách 1: Rút gọn biểu thức $S_n$ dựa vào việc phân tích phần tử đại diện.

Với mọi số nguyên dương , ta có $\frac{1}{(2k-1)(2k+1)}$$=\frac{1}{2}\left(\frac{1}{2k-1}-\frac{1}{2k+1}\right)$

Do đó:

$S_n$

$=\frac{1}{2}\left(1-\frac{1}{3}+\mathrm{...}+\frac{1}{2n-1}-\frac{1}{2n+1}\right)$

$=\frac{1}{2}\left(1-\frac{1}{2n+1}\right)=\frac{n}{2n+1}$

Vậy phương án đúng là phương án C.

Cách 2. Dùng phương pháp quy nạp chứng minh C đúng.

Đáp án cần chọn là: C

Để chọn được S đúng, chúng ta có thể dựa vào một trong ba cách sau đây:

Cách 1: Kiểm tra tính đúng –sai của từng phương án với những giá trị của .

Với n=1 thì S=1.4 = 4 (loại ngay được phương án B và C).

Với $n=2$ thì 

S =1.4+2.7=18 (loại được phương án D).

Cách 2: Bằng cách tính S trong các trường hợp n= 1, S= 4; n=2, S=18; n= 3, S= 48 ta dự đoán được công thức $S=n{(n+1)}^2$.

Cách 3: Ta tính  dựa vào các tổng đã biết kết quả như $1+2+\mathrm{...}+n=\frac{n(n+1)}{2}$

2 và $1^2+2^2+\mathrm{...}+n^2=\frac{n(n+1)(2n+1)}{6}$

 Ta có:

 $S$$=3(1^2+2^2+\mathrm{...}+n^2)$

$+(1+2+\mathrm{...}+n)$

$=n{(n+1)}^2$

Đáp án cần chọn là: A

Cách 1: Kiểm nghiệm từng phương án đúng đối với những giá trị cụ thể của n.

Với $n=1,S_1=1.1!=1$ (Loại ngay được các phương án A, C, D).

Đáp án cần chọn là: B

Với $n=1$ ta có ${13}^1-1=12⋮12$, ta sử dụng phương pháp quy nạp toán học để chứng minh ${13}^n-1$chia hết cho 12 với mọi $n\in N*$

Giả sử khẳng định trên đúng đến $n=k(k\ge 1)$, tức là $({13}^k-1)⋮12$, ta chứng minh đúng đến $n=k+1$, tức là ${13}^{k+1}-1$ cũng chia hết cho 12

Ta có: ${13}^{k+1}-1={13.13}^k-13+12$

$=13({13}^k-1)+12$

Theo giả thiết quy nạp ta có: $({13}^k-1)⋮12$  và $12⋮12$ nên

$13({13}^k-1)+12⋮12$

$\Rightarrow ({13}^{k+1}-1)⋮12$

Vậy $({13}^n-1)⋮12$, $\forall n\in N*$

Đáp án cần chọn là: C

Với $n=3$ ta loại được đáp án A, B và C.

Ta chứng minh đáp án D đúng bằng phương pháp quy nạp toán học.

Bất đẳng thức $2^n>2n+1$ đúng với $n=3$ vì  vì 8>7.

Giả sử bất đẳng thức đúng đến $n=k\ge 3$, tức là , ta chứng minh bất đẳng thức đúng đến $n=k+1$, tức là cần chứng minh $2^{k+1}>2(k+1)+1=2k+3$

Ta có: $2^{k+1}={2.2}^k>2(2k+1)$

$=4k+2=2k+3+2k-1$

Vì : $k\ge 3\Rightarrow 2k-1\ge 5>0$

Do đó bất đẳng thức đúng đến $n=k+1$

Vậy BĐT đúng với mọi số tự nhiên $n\ge 3$

Đáp án cần chọn là: D

Khi $n=1$ ta có $\frac{1}{\sqrt{1}}=1<2$⇒ Loại đáp án A, B, D.

Ta chứng minh đáp án C đúng bằng phương pháp quy nạp toán học.

Bất đẳng thức đúng với $n=1$.

Giả sử bất đẳng thức đúng đến $n=k(k\ge 1)$ tức là

$1+\frac{1}{\sqrt{2}}+\mathrm{...}+\frac{1}{\sqrt{k}}<2\sqrt{k}$, ta chứng minh bất đẳng thức đúng đến $n=k+1$, tức là cần chứng minh $1+\frac{1}{\sqrt{2}}+\mathrm{...}+\frac{1}{\sqrt{k+1}}<2\sqrt{k+1}$

Ta có: 

VT= $1+\frac{1}{\sqrt{2}}+\mathrm{...}+\frac{1}{\sqrt{k}}+\frac{1}{\sqrt{k+1}}$

$<2\sqrt{k}+\frac{1}{\sqrt{k+1}}$

Giả sử:

$\begin{array}{l}2\sqrt{k}+\frac{1}{\sqrt{k+1}}<2\sqrt{k+1}\\ \iff \frac{1}{\sqrt{k+1}}<2\sqrt{k+1}-2\sqrt{k}\\ =\frac{2}{\sqrt{k+1}+\sqrt{k}}\\ \iff \sqrt{k+1}>\frac{\sqrt{k+1}}{2}+\frac{\sqrt{k}}{2}\\ \iff \frac{\sqrt{k+1}}{2}>\frac{\sqrt{k}}{2}\iff \sqrt{k+1}\text{\hspace{0.17em}\hspace{0.17em}}>\text{\hspace{0.17em}\hspace{0.17em}}\sqrt{k}\end{array}$

(luôn đúng)

Do đó: $2\sqrt{k}+\frac{1}{\sqrt{k+1}}<2\sqrt{k+1}$

$\Rightarrow 1+\frac{1}{\sqrt{2}}+\mathrm{...}+\frac{1}{\sqrt{k+1}}<2\sqrt{k+\text{\hspace{0.17em}\hspace{0.17em}}1}$

Do đó bất đẳng thức đúng đến $n=k+1$

Vậy $1+\frac{1}{\sqrt{2}}+\mathrm{...}+\frac{1}{\sqrt{n}}<2\sqrt{n}$  đúng với mọi số nguyên dương .

Đáp án cần chọn là: C