Câu hỏi:
23/07/2024 1,032Tính tổng:
1.4 + 2.7 + … +n.(3n +1)
A. 
B. 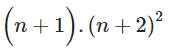
C. 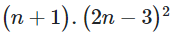
D. Đáp án khác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta dùng phương pháp quy nạp để chứng minh với mọi số nguyên dương n thì:
1.4+2.7+⋅⋅⋅+n(3n+1)
=n(n+1)2 (1)
Với n = 1: Vế trái của (1) = 1. 4 = 4.
Vế phải của (1) =1(1+1)2=4.
Suy ra Vế trái của (1) = Vế phải của (1). Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k . Có nghĩa là ta có:
1.4+2.7+⋅⋅⋅+k(3k+1)
=k(k+1)2 (2)
Ta phải chứng minh (1) đúng với n = k + 1 . Có nghĩa ta phải chứng minh:
1.4+2.7+⋅⋅⋅+k(3k+1)
+(k+1)(3k+4)
=(k+1)(k+2)2
Thật vậy
1.4+2.7+⋅⋅⋅+k(3k+1)⏟=k(k+1)2
+(k+1)(3k+4)
=k(k+1)2+(k+1)(3k+4)
=(k+1).[ k.(k+1)+3k+4]
=(k+1).(k2+4k+4)
=(k+1)(k+2)2 (đpcm).
Vậy (1) đúng khi n = k + 1 . Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Chọn A
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Với mọi số nguyên dương n≥2, ta có: (1-14)(1-19)...(1-1n2)=an+2bn, trong đó a, b là các số nguyên. Tính các giá trị của biểu thức T=a2+b2
Câu 4:
Đặt Sn=11.2+12.3+13.4+...+1n(n+1) với n∈ℕ*. Mệnh đề nào dưới đây đúng
Câu 7:
Đặt Sn=11.3+13.5+...+1(2n-1)(2n+1) với n∈ℕ*. Mệnh đề nào dưới đây đúng
Câu 8:
Dùng quy nạp chứng minh mệnh đề chứa biến P(n) đúng với mọi số tự nhiên n≥p (p là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề P(n) đúng với n=k. Khẳng định nào sau đây là đúng?
Câu 10:
Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến đúng với mọi số tự nhiên n≥p ( p là một số tự nhiên), ta tiến hành hai bước:
- Bước 1, kiểm tra mệnh đề P(n) đúng với n=p
- Bước 2, giả thiết mệnh đề P(n) đúng với số tự nhiên bất kỳ n=k≥p và phải chứng minh rằng nó cũng đúng với n=k+1
Trong hai bước trên:
Câu 11:
Với n∈N* , ta xét các mệnh đề: P :“ 7n + 5 chia hết cho 2”;
Q: “7n+ 5 chia hết cho 3” và R: “7n+ 5 chia hết cho 6”.
Số mệnh đề đúng trong các mệnh đề trên là:
Câu 12:
Một học sinh chứng minh mệnh đề "8n+1 chia hết cho 7, ∀n∈ℕ*" (*) như sau:
Giả sử (*) đúng với n=k tức là 8k+ 1 chia hết cho 7
Ta có: ![]() , kết hợp với giả thiết
, kết hợp với giả thiết ![]() chia hết cho 7 nên suy ra được
chia hết cho 7 nên suy ra được ![]() chia hết cho 7.
chia hết cho 7.
Vậy đẳng thức (*) đúng với mọi n∈ℕ*
Khẳng định nào sau đây là đúng?
Câu 15:
Đối với bài toán chứng minh P(n) đúng với mọi n≥p với p là số tự nhiên cho trước thì ở bước 1 ta cần chứng minh mệnh đề đúng với:


