Trắc nghiệm Toán 10 Bài 3: Hàm số bậc hai
-
622 lượt thi
-
28 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
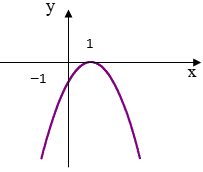
21/07/2024Hình vẽ bên là đồ thị của hàm số nào?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có: Đỉnh I(1,0) và nghịch biến (−∞,1) và (1,+∞).
Câu 2:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có: Vì A,B∈(P)
⇔{5=a.12+b.1+28=a.(−2)2+b.(−2)+2⇒{a=2b=1
Câu 3:
05/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là B
Lời giải
Ta có: Tung độ đỉnh I là f(−b2a)=f(1)=1.
*Phương pháp giải;
Cho parabol (P): y = ax2 + bx + c, ta có:
- Tọa độ đỉnh I của Parabol là 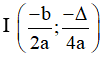 (trong đó Δ = b2 - 4ac)
(trong đó Δ = b2 - 4ac)
*Lý thuyết:
- Khái niệm đường parabol: Một đường parabol là một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
- Phương trình Parabol có dạng: y = ax2 + bx + c
- Gọi I là đỉnh của Parabol ta có 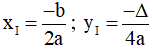 ( trong đó Δ = b2 - 4ac )
( trong đó Δ = b2 - 4ac )
- Phương trình hoành độ giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là: f(x) = g(x).
- Gốc tọa độ có tọa độ là O(0; 0)
- Trục tung có phương trình: x = 0.
- Trục hoành có phương trình: y = 0
Xem thêm
Lý thuyết Hàm số bậc hai – Toán 10 Chân trời sáng tạoCâu 4:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Hàm số đạt GTNN nên loại phương án B và C.
Phương án A: Hàm số có giá trị nhỏ nhất tại nên loại.
Còn lại chọn phương án D.
Câu 5:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có nên hàm số y tăng trên và y giảm trên nên chọn phương án A.
Câu 6:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Hàm số nghịch biến trong khoảng nên loại phương án B và D.
Phương án A: hàm số y nghịch biến trên và y đồng biến trên nên chọn phương án A.
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
.(1)
Mặt khác : Vì
(2)
Kết hợp (1),(2) ta có:
Vậy .
Câu 8:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có: Vì
Vậy
Câu 9:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Gọi (loại đáp án C, D)
Mặt khác:
(thế M từ hai đáp án còn lại vào nhận được với sẽ nhận được ngắn nhất).
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Cho
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Cho
Câu 12:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Cho (1)
Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Đặt ta có:
Câu 14:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có
Vậy nên ta chọn đáp án A.
Câu 15:
19/07/2024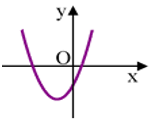
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Nhận xét đồ thị hướng lên nên a>0.
Giao với Oy tại điểm nằm phí dưới trục hoành nên c <0.
Mặt khác Vì a>0 và Đỉnh I nằm bên trái trục hoành nên b>0.
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
Muốn song song với Ox thì có dạng
Nên
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có và
Vậy hàm số giảm trên khoảng và tăng trên khoảng .
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có và
Vậy hàm số tăng trên khoảng và giảm trên khoảng .
Câu 19:
23/07/2024Cho parabol . Khẳng định đúng nhất trong các khẳng định sau là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có và
x=1 là trục đối xứng.
Hàm số f(x) tăng trên khoảng và giảm trên khoảng .
Cắt trục Oy
Câu 20:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có
và
Vậy là trục đối xứng.
Câu 21:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
Để nên
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Parabol (P) cắt Ox tại .
Khi đó
Vậy .
Câu 25:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Vậy .
Câu 26:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phương trình hoành độ giao điểm của hai parabol:
Vậy giao điểm của hai parabol có tọa độ và .
Câu 27:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Parabol (P) đi qua A, B có hoành độ và suy ra và là hai điểm đối xứng nhau qua Oy. Vậy tam giác AOB cân tại O.
Gọi I là giao điểm của AB và Oy vuông tại I nên:
Vậy AOB là tam giác đều.
Cách khác :
,
Vậy nên tam giác AOB là tam giác đều.
Câu 28:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phương trình hoành độ giao điểm của parabol và đường thẳng :
Parabol cắt đường thẳng tại hai điểm phân biệt có hai nghiệm phân biệt
Có thể bạn quan tâm
- Trắc nghiệm Hàm số bậc hai (có đáp án) (621 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (454 lượt thi)
- Trắc nghiệm Toán 10 Bài 3(có đáp án): Hàm số bậc hai (450 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Nhận biết) (461 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Thông hiểu) (560 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Vận dụng) (364 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Tổng hợp) (413 lượt thi)
Các bài thi hot trong chương
- 50 câu trắc nghiệm Hàm số bậc nhất và bậc hai cơ bản (928 lượt thi)
- 50 câu trắc nghiệm Hàm số bậc nhất và bậc hai nâng cao (745 lượt thi)
- Trắc nghiệm Hàm số (có đáp án) (619 lượt thi)
- Trắc nghiệm Ôn tập chương 2 Đại số (có đáp án) (522 lượt thi)
- Trắc nghiệm Hàm số có đáp án (Tổng hợp) (518 lượt thi)
- Trắc nghiệm Hàm số y = ax + b có đáp án (Vận dụng) (499 lượt thi)
- Trắc nghiệm Toán 10 Bài 2(có đáp án): Hàm số y = ax + b (477 lượt thi)
- Trắc nghiệm Hàm số y = ax + b có đáp án (Thông hiểu) (456 lượt thi)
- Trắc nghiệm Hàm số y = ax + b (có đáp án) (452 lượt thi)
- Trắc nghiệm Hàm số y = ax + b có đáp án (421 lượt thi)
