Trắc nghiệm Ôn tập chương 2 Đại số (có đáp án)
Trắc nghiệm Toán 10 Đại số Ôn tập chương 2
-
531 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Đường thẳng (Δ):y=x−1 cắt trục Ox tại A(1;0), cắt trục Oy tại B(0;-1)
Tam giác OAB vuông tại O, có :
SΔOAB=12OA.OB=12.|xA|.|yB|=12
Câu 2:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Đường thẳng (Δ):y=2x−3 cắt trục Ox tại A(32;0), cắt trục Oy B(0;−1)
Tam giác OAB vuông tại O, có SΔOAB=12OA.OB
=12.|xA|.|yB|=12.32.3=94
Câu 3:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đồ thị hàm số đi qua điểm
A(−2;2)⇒y(−2)=2
⇔2=−2(m−1)+3m−2⇔m=2
Câu 4:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Đồ thị hàm số y=ax+b đi qua điểm
{A(0;1)B(1;2)⇒{b=1a+b=2
⇔a=b=1
⇒y=x+1
Câu 5:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Vì đường thẳng (d):y=ax+b có hệ số góc k=−2
suy ra a=−2⇒y=−2x+b. Mà (d) đi qua điểm A(−3;1)→y(−3)=1
⇔−2.(−3)+b=1⇔b=−5.
Vậy y=−2x−5
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Đường thẳng Δ cắt trục hoành tại điểm 2
Câu 7:
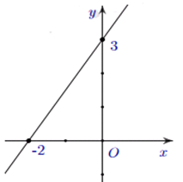
23/07/2024Cho hàm số y=ax+b có đồ thị là hình bên. Giá trị của a và b là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Dựa vào hình vẽ, ta thấy đồ thị hàm số y=ax+b đi qua hai điểm A(−2;3),B(0;3). Do đó:
{y(−2)=0y(0)=3⇔{−2a+b=0b=3⇔{a=b2b=3⇒y=32x+3
Câu 8:
06/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
* Lời giải:
Dễ thấy hàm số y=−πx+3 có hệ số a=−π<0 nên hàm số nghịch biến trên ℝ.
* Phương pháp giải:
- Hàm số bậc nhất xác định bởi mọi x ∈ℝ .
- Hàm số bậc nhất đồng biến trên ℝ khi a > 0.
- Hàm số bậc nhất nghịch biến trên ℝ khi a < 0.
* Một số lý thuyết liên quan:
1. Khái niệm về tính đồng biến, nghịch biến
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc ℝ .
- Nếu giá trị của biến x tăng lên mà giá trị y = f(x) tương ứng cũng tăng thì hàm số y = f(x) là hàm số đồng biến trên ℝ .
- Nếu giá trị của biến x tăng lên mà giá trị của y = f(x) tương ứng giảm thì hàm số y = f(x) là hàm số nghịch biến trên ℝ .
2. Công thức xét tính đồng biến, nghịch biến
Cách 1: Dựa vào khái nệm
Với x1, x2 bất kì thuộc :
- Nếu x1<x2 và f(x1)<f(x2) thì hàm số y = f(x) đồng biến trên ℝ .
- Nếu x1<x2 và f(x1)>f(x2) thì hàm số y = f(x) nghịch biến trên ℝ .
Cách 2: Xét dấu của giá trị T
Để xét tính đồng biến, nghịch biến của hàm số y = f(x), ta xét dấu của T, với T=f(x2)−f(x1)x2−x1 và x1,x2∈ℝ
Nếu T < 0 thì hàm số nghịch biến trên ℝ .
Nếu T > 0 thì hàm số đồng biến trên ℝ .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hàm số bậc nhất (mới 2024 + Bài Tập) – Toán 9
TOP 40 câu Trắc nghiệm Hàm số bậc nhất (có đáp án 2024) – Toán 9
Lý thuyết Các khái niệm về hàm số (mới 2024 + Bài Tập) – Toán 9
Câu 9:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Đồ thị hàm số đi qua
{M(−1;3)N(1;2)⇒{y(−1)=3y(1)=2
⇔{−a+b=3a+b=2⇔(a;b)=(−12;52)
Câu 10:
23/07/2024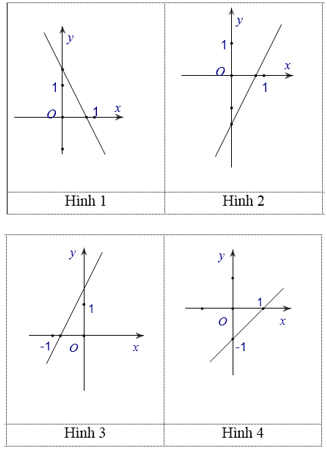
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Đồ thị hàm số y=2x−32 cắt trục Ox tại điểm có hoành độ nhỏ hơn 1, cắt trục Oy tại điểm cực âm. Do đó, chỉ có Hình 2 thỏa mãn.
Câu 11:
23/07/2024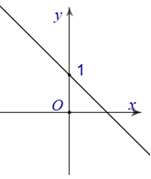
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Dựa vào hình vẽ, ta thấy rằng:
1. Đồ thị hàm số đi qua điểm A(1;0)
2. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ . Suy ra chỉ có đồ thị hàm số y=−x+1 thỏa mãn.
Câu 12:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Xét:
y=ax2+bx+c=a(x2+2.x.b2a+b4a2)+c−b4a=a(x+b2a)−b−4ac4a
Phương trình:
y=0⇔ax2+bx+c=0→Δ=b2−4ac
Do đó, tọa độ đỉnh I(−b2a;−Δ4a)
Câu 13:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Phương trình hoành độ giao điểm của (P) và Ox là ax2+bx+c=0→Δ=b2−4ac.Vì chưa biết hệ số a,b,c nên ta chưa thể đánh giá Δ dương hay âm.
Do đó, đồ thị (P) có thể tiếp xúc , cắt hoặc không cắt trục hoành.
Câu 14:
18/07/2024Cho hàm số y=x2−2x có đồ thị (P). Tọa độ đỉnh của (P) là :
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có (P):y=x2−2x=(x−1)2−1 suy ra tọa độ đỉnh của (P) là I(1;−1)
Câu 15:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Parabol:
y=2x2+6x+3I(−32;−32)
→x=−32 là trục đối xứng của (P)
Câu 16:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có
x2−4x=−x−2⇔[x=1⇒y=−3x=2⇒y=−4
Câu 17:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có
{2x2−5x+3=x+2⇔2x2−6+12x2−5x+3=−x−1⇔2x2−4x+4=02x2−5x+3=x+3⇔2x2−6x=02x2−5x+3=−x+1⇔2x2+4x+2=0
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có
x2−x−6=0⇔[x=−2⇒y=0x=3⇒y=0
Câu 19:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có
x2−2x=m⇔x2−2x−m=0 (1)
YCBT (1) có 2 nghiệm phân biệt
⇔Δ'
Câu 20:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có
Câu 21:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
HD: Ta có
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có
Câu 23:
21/07/2024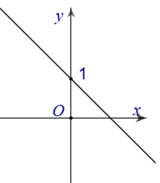
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đồ thị hàm số đi qua điểm (0;1) Loại A và B
Đồ thị hàm số qua điểm (1;0)
Câu 24:
22/07/2024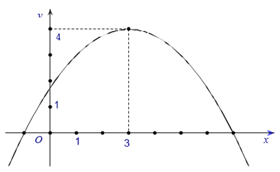
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng Loại A
Đỉnh I(3;4) Loại B
Trục tung x=0, ta có y>0sai
Hiển nhiên D đúng.
Câu 25:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Hàm số có tập xác định D = ℝ.
hàm số chẵn.
Hàm số có tập xác định D = ℝ.
hàm số chẵn.
Hàm số có tập xác định D = ℝ.
hàm số chẵn.
Hàm số có tập xác định D = ℝ.
Câu 26:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Hàm số có tập xác định D = ℝ.
hàm số chẵn.
Hàm số có tập xác định D = ℝ \ {0}.
hàm số lẻ.
Hàm số có tập xác định D = ℝ.
hàm số chẵn.
Hàm số có tập xác định D = ℝ.
Câu 27:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có
Câu 28:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có
Câu 29:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có:
Câu 30:
23/07/2024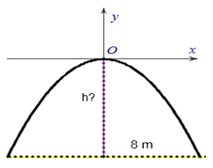
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Đường thẳng chứa chiều rộng d = 8m cắt (P) tại A(4;-h)
Điểm
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 2 Đại số (có đáp án) (530 lượt thi)
- 50 câu trắc nghiệm Hàm số bậc nhất và bậc hai cơ bản (958 lượt thi)
- 50 câu trắc nghiệm Hàm số bậc nhất và bậc hai nâng cao (762 lượt thi)
- Trắc nghiệm Ôn tập chương 2 Hàm số bậc nhất và bậc hai có đáp án (405 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 có đáp án (Nhận biết) (310 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 có đáp án (Thông hiểu) (355 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 có đáp án (Vận dụng) (293 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 có đáp án (Tổng hợp) (361 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Hàm số (có đáp án) (641 lượt thi)
- Trắc nghiệm Hàm số bậc hai (có đáp án) (639 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Thông hiểu) (577 lượt thi)
- Trắc nghiệm Hàm số có đáp án (Tổng hợp) (553 lượt thi)
- Trắc nghiệm Hàm số y = ax + b có đáp án (Vận dụng) (510 lượt thi)
- Trắc nghiệm Toán 10 Bài 2(có đáp án): Hàm số y = ax + b (500 lượt thi)
- Trắc nghiệm Toán 10 Bài 3(có đáp án): Hàm số bậc hai (473 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (Nhận biết) (470 lượt thi)
- Trắc nghiệm Hàm số bậc hai có đáp án (468 lượt thi)
- Trắc nghiệm Hàm số y = ax + b (có đáp án) (466 lượt thi)
