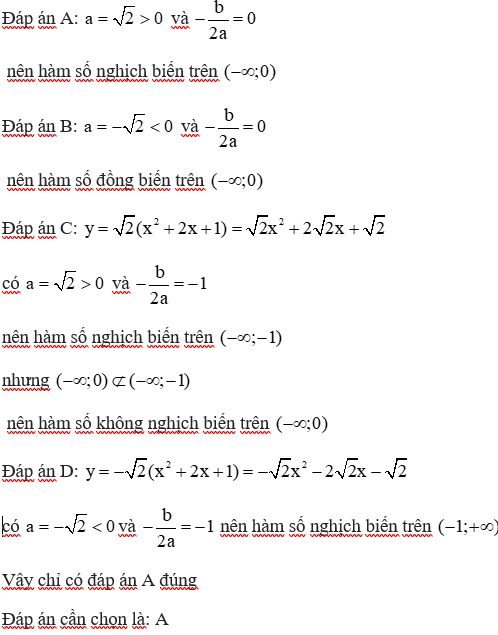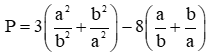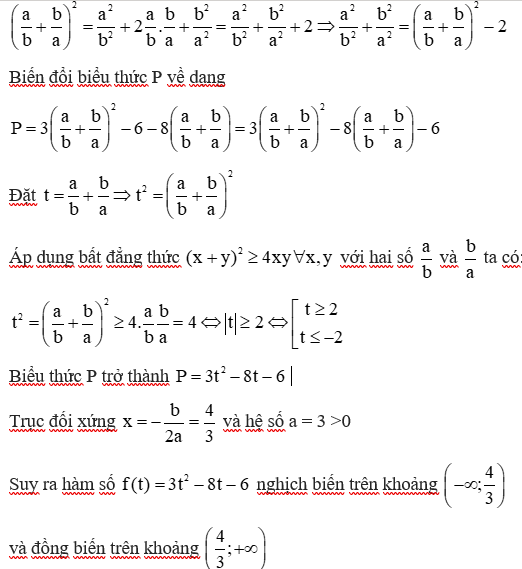37 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hàm số bậc hai có đáp án (Tổng hợp)

Trục đối xứng của parabol $y = - 2 x^{2} + 5 x + 3$ là:

A. $x = \frac{- 5}{2}$

B. $y = \frac{- 5}{4}$

C. $x = \frac{5}{2}$

D. $x = \frac{5}{4}$

Xem đáp án

Trục đối xứng $x = \frac{- b}{2 a} = \frac{5}{4}$

Đáp án cần chọn là: D

Câu 3:

Đỉnh của parabol (P): y = 3x²- 2x + 1 là:

A. I $(\frac{- 1}{3}; \frac{2}{3})$

B. I $(\frac{- 1}{3}; \frac{- 2}{3})$

C. I $(\frac{1}{3}; \frac{- 2}{3})$

D.I $(\frac{1}{3}; \frac{2}{3})$

Xem đáp án

Parabol (P) có hoành độ đỉnh

$x = \frac{- b}{2 a} = - \frac{- 2}{2.3} = \frac{1}{3} \Rightarrow y = 3 . {(\frac{1}{3})}^{2} - 2 . \frac{1}{3} + 1 = \frac{2}{3}$

Vậy đỉnh I $(\frac{1}{3}; \frac{2}{3})$

Đáp án cần chọn là: D

Câu 4:

13/07/2024

Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?

A.y = 2x²+ 2x − 1.

B.y = 2x²+ 2x + 2.

C.y = −2x²− 2x.

D.y = −2x²− 2x + 1.

Xem đáp án

Nhận xét:

Bảng biến thiên có bề lõm hướng xuống. Loại đáp án A và B.

Đỉnh của parabol có tọa độ là ( $(\frac{- 1}{2}; \frac{3}{2})$ ). Xét các đáp án còn lại, đáp án D thỏa mãn.

Đáp án cần chọn là: D

Câu 5:

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x²− 4x + 3 trên đoạn [−2; 1].

A. M = 15; m = 1.

B.M = 15; m = 0.

C.M = 1; m = −2.

D.M = 0; m = −15.

Xem đáp án

Hàm số có a = 1 > 0 nên bề lõm hướng lên

Đáp án cần chọn là: B

Câu 6:

Cho parabol (P): y = −3x²+ 6x − 1. Khẳng định đúng nhất trong các khẳng định sau là:

A.(P) có đỉnh I (1; 2)

B.(P) có trục đối xứng x = 1

C. (P) cắt trục tung tại điểm A (0; −1)

D.Cả a, b, c đều đúng

Xem đáp án

- Ta có a = −3 < 0 và x= $\frac{- b}{2 a}$ = 1 ⇒ I (1, 2)

- Đường thẳng x = 1 là trục đối xứng.

Đáp án cần chọn là: D

- Đồ thị hàm số cắt trục Oy ⇒ x = 0 ⇒ y = −1.

Câu 7:

Tìm giá trị nhỏ nhất y_min của hàm số y = x² – 4x + 5

A.y_min = 0

B.y_min = -2

C. y_min = 2

D. y_min = 1

Xem đáp án

Ta có y = x²− 4x + 5 = (x − 2)²+ 1 ≥ 1 ⇒ y_min= 1 ⇒ y_min= 1

Đáp án cần chọn là: D

Câu 8:

18/07/2024

Cho hàm số y = −x²+ 4x + 1. Khẳng định nào sau đây sai?

A.Hàm số nghịch biến trên khoảng (2; +∞) và đồng biến trên khoảng (−∞; 2).

B.Hàm số nghịch biến trên khoảng (4; +∞) và đồng biến trên khoảng (−∞; 4).

C. Trên khoảng (−∞; −1) hàm số đồng biến

D. Trên khoảng (3; +∞) hàm số nghịch biến

Xem đáp án

Ta có $\frac{- b}{2 a} = 2$ . Do đó hàm số nghịch biến trên khoảng (2; +∞) và đồng biến trên khoảng (−∞; 2). Do đó A đúng, B sai.

Đáp án C đúng vì hàm số đồng biến trên khoảng (−∞; 2) thì đồng biến trên khoảng con (−∞; −1).

Đáp án D đúng vì hàm số nghịch biến trên khoảng (2; +∞) thì nghịch biến trên khoảng con (3; +∞).

Đáp án cần chọn là: B

Câu 9:

Hàm số nào sau đây nghịch biến trong khoảng (- $\infty; 0$ )?

A. $y = \sqrt{2} x^{2} + 1$

B. $y = - \sqrt{2} x^{2} + 1$

C. $y = \sqrt{2} {(x + 1)}^{2}$

D. $y = - \sqrt{2} {(x + 1)}^{2}$

Xem đáp án

Câu 10:

Cho hàm số y = ax²+ bx + c có đồ thị (P) như hình vẽ.

Khẳng định nào sau đây là sai?

A.Hàm số đồng biến trên khoảng (−∞; 3).

B.(P) có đỉnh là I (3; 4).

C.(P) cắt trục tung tại điểm có tung độ bằng 1.

D. (P) cắt trục hoành tại hai điểm phân biệt.

Xem đáp án

Đồ thị hàm số đi lên trên khoảng (−∞; 3) nên đồng biến trên khoảng đó. Do đó A đúng.

Dựa vào đồ thị ta thấy (P) có đỉnh có tọa độ (3; 4). Do đó B đúng.

(P) cắt trục hoành tại hai điểm phân biệt có hoành độ −1 và 7. Do đó D đúng.

Dùng phương pháp loại trừ thì C là đáp án sai.

Đáp án cần chọn là: C

Câu 11:

15/07/2024

Parabol (P): y = x² + 4x + 4 có số điểm chung với trục hoành là:

A. 0

B.1

C.2

D.3

Xem đáp án

Phương trình hoành độ giao điểm của (P) với trục hoành là x²+ 4x + 4 = 0

⇔ (x + 2)²= 0 ⇔ x = −2.

Vậy (P) có 1 điểm chung với trục hoành.

Đáp án cần chọn là: B

Câu 12:

20/07/2024

Khi tịnh tiến parabol y = 2x² sang trái 3 đơn vị, ta được đồ thị của hàm số:

A.y = 2(x + 3)²

B.y = 2x²+ 3

C. y = 2(x − 3)².

D. y = 2x²− 3.

Xem đáp án

Tịnh tiến đồ thị hàm số y = 2x² sang trái 3 đơn vị ta được đồ thị hàm số

y = 2.(x + 3)².

Đáp án cần chọn là: A

Câu 13:

20/07/2024

Nếu hàm số y = ax²+ bx + c có a < 0, b > 0 và c > 0 thì đồ thị của nó có dạng

A

B.

C.

D.

Xem đáp án

+ a < 0 nên loại đáp án A, B.

+ c > 0 nên giao điểm của đồ thị với trục tung có tung độ dương, chọn đáp án D.

Ngoài ra các em cũng có thể nhận xét vì b > 0, a < 0 nên hoành độ đỉnh $\frac{- b}{2 a} > 0$ và đáp án D thỏa mãn.

Đáp án cần chọn là: D

Câu 14:

Cho hàm số y = ax²+ bx + c có đồ thị như hình bên.

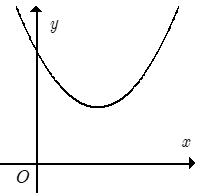
Khẳng định nào sau đây đúng?

A. a > 0, b < 0, c < 0.

B.a > 0, b < 0, c > 0.

C.a > 0, b > 0, c > 0.

D.a < 0, b < 0, c > 0.

Xem đáp án

Bề lõm hướng lên nên a > 0.

Hoành độ đỉnh parabol x = - $\frac{- b}{2 a}$ > 0 nên b < 0.

Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.

Đáp án cần chọn là: B

Câu 15:

Cho hàm số y = ax²+ bx + c có đồ thị như hình bên.

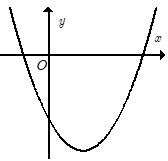
Khẳng định nào sau đây đúng ?

A. a > 0, b < 0, c < 0.

B.a > 0, b < 0, c > 0.

C. a > 0, b > 0, c > 0.

D. a < 0, b < 0, c > 0.

Xem đáp án

Bề lõm hướng lên nên a > 0.

Hoành độ đỉnh parabol x = - $\frac{- b}{2 a}$ nên b < 0.

Parabol cắt trục tung tại điểm có tung độ âm nên c < 0.

Đáp án cần chọn là: A

Câu 16:

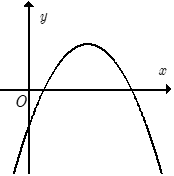
Cho hàm số y = ax²+ bx + c có đồ thị như hình bên. Khẳng định nào sau đây đúng ?

A. a > 0, b > 0, c < 0.

B.a > 0, b < 0, c > 0.

C.a < 0, b > 0, c < 0.

D.a < 0, b > 0, c > 0.

Xem đáp án

Bề lõm hướng xuống nên a < 0.

Hoành độ đỉnh parabol x = - $\frac{- b}{2 a}$ >0 nên b > 0.

Parabol cắt trục tung tại điểm có tung độ âm nên c < 0.

Đáp án cần chọn là: C

Câu 17:

Cho hàm số y = ax²+ bx + c (a > 0). Khẳng định nào sau đây là sai?

A. Hàm số đồng biến trên khoảng (− ; +∞).

B. Hàm số nghịch biến trên khoảng (−∞;− ).

C.Đồ thị của hàm số có trục đối xứng là đường thẳng x =− $\frac{- b}{2 a}$ .

D.Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt

Xem đáp án

Ví dụ trường hợp đồ thị có đỉnh nằm phía trên trục hoành thì khi đó đồ thị hàm số không cắt trục hoành.

(Hoặc xét phương trình hoành độ giao điểm ax²+ bx + c = 0, phương trình này không phải lúc nào cũng có hai nghiệm).

Đáp án cần chọn là: D

Câu 18:

20/07/2024

Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = −3x²− 6x.

B. y = 3x²+ 6x + 1.

C. y = x²+ 2x + 1.

D.y = −x²− 2x + 1.

Xem đáp án

Nhận xét: Parabol có bề lõm hướng lên. Loại đáp án A, D.

Parabol cắt trục hoành tại 2 điểm phân biệt có hoành độ âm. Xét các đáp án B và C, đáp án B thỏa mãn

Đáp án cần chọn là: B

Câu 19:

Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y = x^{2} - 2 x + \frac{3}{2}$

A.

B. $y = \frac{- 1}{2} x^{2} + x + \frac{5}{2}$

C. $y = x^{2} - 2 x$

D. $y = \frac{- 1}{2} x^{2} + x + \frac{3}{2}$

Xem đáp án

Nhận xét:

Parabol có bề lõm hướng xuống. Loại đáp án A, C.

Parabol cắt trục hoành tại 2 điểm (3; 0) và (−1; 0). Xét các đáp án B và D, đáp án D thỏa mãn.

Đáp án cần chọn là: D

Câu 20:

Xác định parabol (P): y = 2x²+ bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.

A. y = 2x²− 4x + 4.

B.y = 2x²+ 4x − 3.

C.y = 2x²− 3x + 4.

D.y = 2x²+ x + 4.

Xem đáp án

Ta có M ∈ (P) ⇒ c = 4

Trục đối xứng − $\frac{- b}{2 a}$ = 1 ⇒ b = −4.

Vậy (P): y = 2x²− 4x + 4.

Đáp án cần chọn là: A

Câu 21:

14/07/2024

Xác định Parabol (P): $y = a x^{2} + b x + 3$ biết rằng Parabol có đỉnh I (3; -2)

A. $y = x^{2} - 6 x + 3$

B. $y = \frac{- 5}{9} x^{2} + \frac{10}{3} x + 3$

C. $y = 3 x^{2} + 9 x + 3$

D. $y = \frac{5}{9} x^{2} - \frac{10}{3} x + 3$

Xem đáp án

Ta có đỉnh của (P) có tọa độ

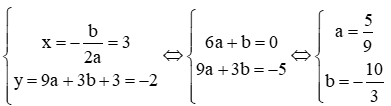
Suy ra phương trình của Parabol (P) là: $y = \frac{5}{9} x^{2} - \frac{10}{3} x + 3$

Đáp án cần chọn là: D

Câu 22:

Tìm parabol (P): y = ax²+ 3x − 2, biết rằng parabol có đỉnh I $(\frac{- 1}{2}; \frac{- 11}{4})$

A. y = x²+ 3x − 2.

B.y = x²+ x − 4.

C.y = 3x²+ x − 1.

D. y = 3x²+ 3x − 2.

Xem đáp án

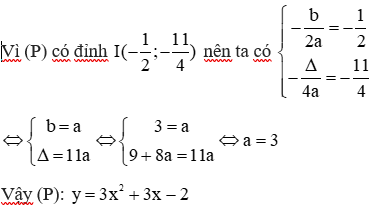
Đáp án cần chọn là: D

Câu 23:

14/07/2024

Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A (0; 2), B (-2; 5), C (3; 8)

A. $y = \frac{7}{10} x^{2} + \frac{1}{10} x - 2$

B. $y = \frac{7}{10} x^{2} + \frac{1}{10} - 2$

C. $y = \frac{7}{10} x^{2} - \frac{1}{10} - 2$

D. $y = \frac{7}{10} x^{2} + \frac{1}{10} + 2$

Xem đáp án

Đáp án cần chọn là: B

Câu 24:

18/07/2024

Tìm các giá trị thực của tham số m để phương trình |x²− 3x + 2| = m có bốn nghiệm thực phân biệt.

A. $m \geq \frac{- 1}{4}$

B. $0 < m < \frac{1}{4}$

C. m = 0

D.Không tồn tại

Xem đáp án

Số nghiệm của phương trình đã cho bằng số giảo điểm của đồ thị hàm số

y = |x²− 3x + 2| với đường thẳng y = m có tính chất song song với trục hoành.

Ta có y = |x²− 3x + 2|=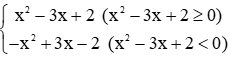

Đồ thị hàm số y = |x²− 3x + 2| được vẽ như sau:

+ Vẽ đồ thị hàm số y = x²− 3x + 2

+ Lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa phần đồ thị dưới trục hoành đi.

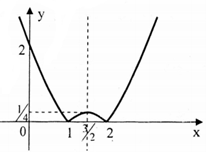
Dựa trên đồ thị ta thấy phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi

0 < m < $\frac{1}{4}$ .

Đáp án cần chọn là: B

Câu 25:

17/07/2024

Cho hàm số f(x) = ax²+ bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.

A. 0 < m < 1.

B.m > 3.

C.m = −1, m = 3.

D. −1 < m < 0.

Xem đáp án

Từ đó suy ra cách vẽ đồ thị hàm số (C) từ đồ thị hàm số y = f(x) như sau:

+ Giữ nguyên đồ thị y = f(x) phía trên trục hoành.

+ Lấy đối xứng phần đồ thị y = f(x) phía dưới trục hoành qua trục hoành (bỏ phần dưới).

Kết hợp hai phần ta được đồ thị hàm số y =| f(x)| như hình vẽ.

Phương trình |f(x)| = m là phương trình hoành độ giao điểm của đồ thị hàm số

y = |f(x)| và đường thẳng y = m (song song hoặc trùng với trục hoành).

Dựa vào đồ thị, ta có yêu cầu bài toán ⇔ 0 < m < 1.

Đáp án cần chọn là: A

Câu 26:

Tìm các giá trị của tham số m để phương trình có 3 nghiệm phân biệt

A. $m = 3$

B. $- \sqrt{3} < m < \sqrt{3}$

C. $m = \pm \sqrt{3}$

D. Không tồn tại

Xem đáp án

+ Vẽ hai đồ thị hàm số trên cùng một hệ trục tọa độ.

+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm y = x²− 4x + 3 và xóa nhánh bên trái trục tung.

+ Giữ nguyên nhánh bên trái trục tung của đồ thị hàm số y = x²+ 4x + 3 và xóa nhánh bên phải trục tung của đồ thị hàm số đó.

Dựa trên đồ thị ta thấy phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi m²= 3 ⇔ m = ± $\sqrt{3}$ .

Đáp án cần chọn là: C

Câu 27:

21/07/2024

Tìm các giá trị của m để phương trình $x^{2} - 2 x + \sqrt{4 x^{2} - 12 x + 9} = m$ acó nghiệm duy nhất

A. $\frac{- 3}{4} < m < 0$

A.

B. $\frac{- \sqrt{3}}{2} < m < \frac{\sqrt{3}}{2}$

C. $m = \frac{- 3}{4}$

D. Không tồn tại

Xem đáp án

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số

y = x²− 2x + |2x − 3| và đường thẳng y = m có tính chất song song với trục hoành.

Đồ thị hàm số

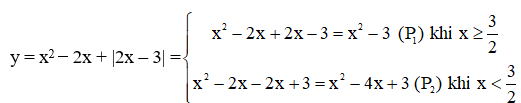
được vẽ như sau:

+ Vẽ lần lượt hai đồ thị hàm số trên cùng một hệ trục tọa độ

+ Xóa đi nhánh bên trái điểm $x = \frac{3}{2}$ của đồ thị hàm số y = x²− 3

+ Xóa đi nhánh bên phải điểm $x = \frac{3}{2}$ của đồ thị hàm số y = x²− 4x + 3

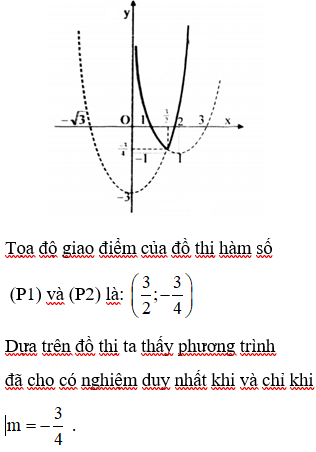
Đáp án cần chọn là: C

Câu 28:

17/07/2024

Cho phương trình của (P): y = ax²+ bx + c (a ≠ 0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tính tổng a²+ b²+ c².

A. a²+ b²+ c² = 3

B. a²+ b²+ c² = $\frac{29}{16}$

C. a²+ b²+ c² = $\frac{48}{29}$

D.

Xem đáp án

Dễ thấy rằng đồ thị của (P) có đỉnh đặt trên đường thẳng y = 1 và hệ số m < 0.

Do đó, phương trình của (P) có dạng y = m(x − u)²+ 1 (m < 0).

(P)đi qua các điểm A (2; 0), B (−2; −8) nên có hệ phương trình

Câu 29:

13/07/2024

Biết rằng hàm số y = ax²+ bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 5 tại x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = a²+ b²+ c².

A. S = −1.

A.

B. S=1

C.S=13

D. S=14

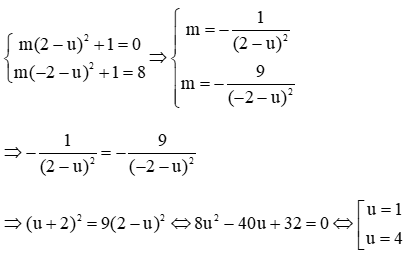
Xem đáp án

Câu 30:

Tìm các giá trị của tham số m để $2 x^{2} - 2 (m + 1) x + m^{2} - 2 m + 4 \geq 0 (\forall x)$

A.m=3

B. $3 - \sqrt{2} < m < 3 + \sqrt{2}$

C.

D.Không tồn tại

Xem đáp án

Yêu cầu bài toán tương đương tìm giá trị của m để đồ thị hàm số (P): y = 2x²– 2(m+1)x + m²− 2m + 4 luôn nằm phía trên trên trục hoành.

Suy ra với giá trị x₀ thì giá trị nhỏ nhất của hàm số đã cho lớn hơn hoặc bằng 0.

Parabol có hệ số a = 2 > 0 nên có bề lõm hướng lên trên đạt GTNN tại đỉnh parabol $x = \frac{m + 1}{2}$

Câu 31:

Tìm giá trị nhỏ nhất của hàm số f(x) biết rằng $f (x + 2) = x^{2} - 3 x + 2$

A. $\frac{- 1}{4}$

B. $\frac{1}{4}$

C. $\frac{1}{2}$

D.0

Xem đáp án

Đặt t = x + 2 ⇒ x = t − 2, từ đẳng thức trên ta suy ra f(t) = (t − 2)²− 3(t − 2) + 2 = t²− 7t + 12.

Suy ra f(x) = x²− 7x + 12 = ${(x - \frac{7}{2})}^{2} - \frac{1}{4} \geq \frac{- 1}{4}$ ∀x∈R

Vậy Min f(x) = − $\frac{1}{4}$ khi x = $\frac{7}{2}$

Đáp án cần chọn là: A

Câu 32:

16/07/2024

Tìm giá trị của m để hàm số y = −x²+ 2x + m − 5 đạt giá trị lớn nhất bằng 6

A. m=0

B. m=10

C.m=-10

D. Không xác định được

Xem đáp án

Hàm số đã cho đạt giá trị lớn nhất tại x = $\frac{- b}{2 a}$ =1.

Khi đó max y = f(1) = m − 4

Để max y = 6 thì m – 4 = 6 ⇔ m = 10

Đáp án cần chọn là: B

Câu 33:

21/07/2024

Biết rằng hàm số y = ax²+ bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.

A. P = −6

B. P = 6.

C. P = −3.

D. P = 32

Xem đáp án

Câu 34:

Tìm giá trị của m để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ dương

A.

B.

C.1<m<2

D. Không xác định được

Xem đáp án

Xét phương trình hoành độ giao điểm x²− 2x + m – 1 = 0 (∗). Để đồ thị hàm số y = x²− 2x + m − 1 cắt trục hoành tại hai điểm phân biệt có hoành độ dương thì phương trình (*) có 2 nghiệm dương phân biệt.

Đáp án cần chọn là: A

Câu 35: