Câu hỏi:
18/07/2024 803Cho hàm số y = −x2 + 4x + 1. Khẳng định nào sau đây sai?
A.Hàm số nghịch biến trên khoảng (2; +∞) và đồng biến trên khoảng (−∞; 2).
B.Hàm số nghịch biến trên khoảng (4; +∞) và đồng biến trên khoảng (−∞; 4).
C. Trên khoảng (−∞; −1) hàm số đồng biến
D. Trên khoảng (3; +∞) hàm số nghịch biến
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có . Do đó hàm số nghịch biến trên khoảng (2; +∞) và đồng biến trên khoảng (−∞; 2). Do đó A đúng, B sai.
Đáp án C đúng vì hàm số đồng biến trên khoảng (−∞; 2) thì đồng biến trên khoảng con (−∞; −1).
Đáp án D đúng vì hàm số nghịch biến trên khoảng (2; +∞) thì nghịch biến trên khoảng con (3; +∞).
Đáp án cần chọn là: B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên. Khẳng định nào sau đây đúng ?
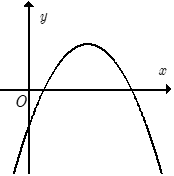
Câu 2:
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 3:
Nếu hàm số y = ax2 + bx + c có a < 0, b > 0 và c > 0 thì đồ thị của nó có dạng
Câu 4:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
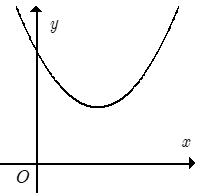
Khẳng định nào sau đây đúng?
Câu 5:
Cho hàm số f(x) = ax2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
Câu 6:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 5 tại x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = a2 + b2 + c2.
Câu 7:
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 8:
Cho parabol (P): y = −3x2 + 6x − 1. Khẳng định đúng nhất trong các khẳng định sau là:
Câu 9:
Xác định parabol (P): y = 2x2 + bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.
Câu 10:
Cho hàm số y = ax2 + bx + c có đồ thị (P) như hình vẽ.
Khẳng định nào sau đây là sai?
Câu 13:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên.
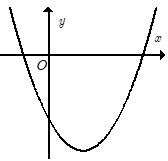
Khẳng định nào sau đây đúng ?
Câu 14:
Cho hàm số y = ax2 + bx + c (a > 0). Khẳng định nào sau đây là sai?
Câu 15:
Tìm giá trị của m để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ dương


