20 câu hỏi trắc nghiệm thuộc 75 câu trắc nghiệm Bất đẳng thức

Câu 1:

18/07/2024

Cho bất phương trình $|\frac{2}{x - 13}| > \frac{8}{9}$

Các nghiệm nguyên nhỏ hơn 13 của bất phương trình là

A. x = 7 và x = 8

B. x = 9 và x = 10

C. x = 11 và x = 12

D. x = 14 và x = 15

Xem đáp án

Chọn C

Câu 2:

18/07/2024

Xét dấu của các biểu thức sau :

f(x) = ( -x²+x-1)(6x²-5x+1)

A. f(x) > 0 khi và chỉ khi $x \in (\frac{1}{3}; \frac{1}{2})$

B. f(x) < 0 khi và chỉ khi $x \in (\frac{1}{3}; \frac{1}{2})$

C. f(x)>0 khi và chỉ khi $x \in (- \infty; \frac{1}{3}) \cup (\frac{1}{2}; + \infty)$

D. f(x)< 0 khi và chỉ khi $x \in (- \infty; \frac{1}{3})$

Xem đáp án

Chọn A

Ta có –x²+x-1= 0 vô nghiệm,

6x²- 5x+1= 0 khi x= ½ hoặc x= 1/3

Bảng xét dấu

Suy ra f(x) > 0 khi và chỉ khi Xét dấu của các biểu thức sau f(x) = (-x^2 + x - 1)(6x^2 - 5x +1) (ảnh 2)

Và f( x)< 0 khi và chỉ khi Xét dấu của các biểu thức sau f(x) = (-x^2 + x - 1)(6x^2 - 5x +1) (ảnh 3)

Câu 3:

22/07/2024

Cho biểu thức $g (x) = \frac{x^{2} - x - 2}{- x^{2} + 3 x + 4}$

Tìm mệnh đề đúng ?

A. g(x) < 0 khi và chỉ khi 2<x< 4

B. g(x) > 0 khi và chỉ khi 2<x< 4

C. g(x) > 0 khi và chỉ khi x ∈ (-∞;-1)∪(-1;-2)

D. g(x) < 0 khi và chỉ khi x ∈ (-1;-2)∪(4;+∞)

Xem đáp án

Chọn B

Ta có x²-x-2= 0 khi x= -1 hoặc x=2;

-x²+3x+4=0 khi x= -1 hoặc x= 4

Bảng xét dấu

Suy ra g(x) > 0 khi và chỉ khi 2< x< 4

Và g(x) < 0 khi và chỉ khi x ∈ (-∞;-1)∪(-1;2)∪( 4;+∞).

Câu 4:

21/07/2024

Cho biểu thức h(x) = x³-5x+2

A. h(x)<0 khi và chỉ khi

B. h(x)>0 khi và chỉ khi

C. h(x)<0 khi và chỉ khi

D. h(x >0 khi và chỉ khi

Xem đáp án

Chọn D

Ta có x³-5x+2 = (x-2)( x²+2x-1)

Và x²+2x-1= 0 khi và chỉ khi

Bảng xét dấu

Cho biểu thức h(x) = x^3 - 5x + 2 h(x)<0 khi và chỉ khi (ảnh 2)

Suy ra h( x) > 0 khi và chỉ khi

và h(x) < 0 khi và chỉ khi

Câu 5:

18/07/2024

Cho biểu thức $f (x) = x - \frac{x^{2} - x + 6}{- x^{2} + 3 x + 4}$

Tìm mệnh đề đúng?

A. f(x) > 0 khi và chỉ khi

B. f(x) > 0 khi và chỉ khi

C. f( x) < 0 khi và chỉ khi

D. f(x) < 0 khi và chỉ khi

Xem đáp án

Chọn D

+Ta có

+ lại có: -x²+x+6= 0 khi x=-2 hoặc x = 3;

-x²+3x+4= 0 khi x= -1 hoặc x= 4

Bảng xét dấu

Cho biểu thức f(x) = x - (x^2 - x + 6)/(-x^2 + 3x + 4) Tìm mệnh đề đúng (ảnh 2)

Suy ra f(x) > 0 khi và chỉ khi

Và f(x) < 0 khi và chỉ khi

Câu 6:

22/07/2024

Xét dấu các biểu thức sau:

$f (x) = \frac{1}{x + 9} - \frac{1}{x} - \frac{1}{2}$

A.

B.

C.

D.

Xem đáp án

Chọn B

Ta có:

$f (x) = \frac{1}{x + 9} - \frac{1}{x} - \frac{1}{2} \Leftrightarrow f (x) = \frac{2 x}{2 x (x + 9)} - \frac{2 (x + 9)}{2 x (x + 9)} - \frac{x (x + 9)}{2 x (x + 9)} \Leftrightarrow f (x) = \frac{2 x - 2 x - 18 - x^{2} - 9 x}{2 x (x + 9)} \Leftrightarrow f (x) = \frac{- x^{2} - 9 x - 18}{2 x (x + 9)}$

Đa thức $- x^{2} - 9 x - 18$ có hai nghiệm x = -6 và x = -3; x có nghiệm x = 0; x+2 có nghiệm x = -2

Khi đó ta có bảng xét dấu sau:

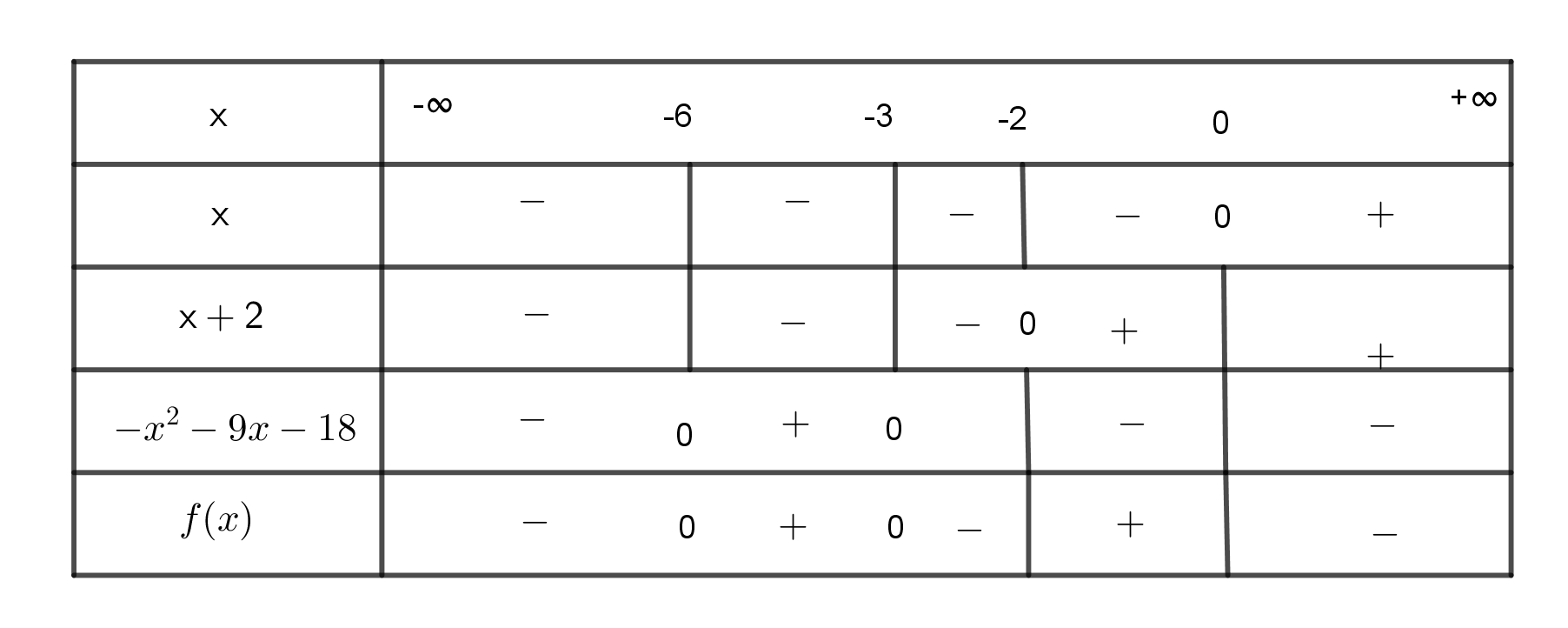
Suy ra $f (x) > 0 \Leftrightarrow x \in (- 6; - 3) \cup (2; 0)$

$f (x) < 0 \Leftrightarrow x \in (- \infty; - 6) \cup (- 3; 2) \cup (0; + \infty)$

Câu 7:

15/12/2024

Xét dấu của biểu thức sau : f(x) = x⁴ – 4x + 1

A. Xét dấu của biểu thức sau f(x) = x^4 – 4x + 1 (ảnh 2)

B. Xét dấu của biểu thức sau f(x) = x^4 – 4x + 1 (ảnh 3)

C. Xét dấu của biểu thức sau f(x) = x^4 – 4x + 1 (ảnh 4)

D. Xét dấu của biểu thức sau f(x) = x^4 – 4x + 1 (ảnh 5)

Xem đáp án

Đáp án đúng là D

Lời giải

*Phương pháp giải:

Phân tích thành biểu thức bậc 2 rồi xét dấu

*Lý thuyết;

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0).

+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ℝ.

+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi $x \neq - \frac{b}{2 a}$ và $f (- \frac{b}{2 a}) = 0$

+ Nếu ∆ > 0 thì tam thức f(x) có hai nghiệm phân biệt x₁ và x₂ (x₁ < x₂). Khi đó, f(x) cùng dấu với hệ số a với mọi x ∈ (–∞; x₁) ∪ (x₂; +∞); f(x) trái dấu với hệ số a với mọi x ∈ (x₁; x₂).

Tức là, khi ∆ > 0, dấu của f(x) và a là: “Trong trái, ngoài cùng”

Bất phương trình bậc hai

- Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax² + bx + c > 0 (hoặc ax² + bx + c ≥ 0, ax² + bx + c < 0, ax² + bx + c ≤ 0), trong đó a, b, c là những số thực đã cho và a ≠ 0.

- Số thực x₀ gọi là một nghiệm của bất phương trình bậc hai ax² + bx + c > 0, nếu ax₀² + bx₀ + c > 0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax² + bx + c > 0 gọi là tập nghiệm của bất phương trình này.

- Giải một bất phương trình bậc hai là tìm tập nghiệm của nó.

Nhận xét: Để giải bất phương trình bậc hai ax² + bx + c > 0 (hoặc ax² + bx + c ≥ 0, ax² + bx + c < 0, ax² + bx + c ≤ 0) ta cần xét dấu tam ax² + bx + c, từ đó suy ra tập nghiệm.

Xem thêm

Lý thuyết Dấu của tam thức bậc hai - Toán 10 Kết nối tri thức

Trắc nghiệm Dấu của tam thức bậc hai có đáp án – Toán lớp 10

Câu 8:

22/07/2024

Cho biểu thức g(x) = (m-1) x²+2( m-1)x +m-3.

Tùy theo giá trị của tham số m, khẳng định nào sau đây là sai?

A. khi m=1 thì g(x) < 0 mọi x

B. m > 1 thì tam thức g(x) có hai nghiệm phân biệt

C. khi m < 1 thì g(x) < 0 mọi x

D. Cả A, B, C đều sai

Xem đáp án

Chọn D

Câu 9:

17/07/2024

Tìm các giá trị của m để biểu thức sau luôn dương

$h (x) = \frac{- x^{2} + 4 (m + 1) x + 1 - 4 m^{2}}{- 4 x^{2} + 5 x - 2}$

A. m < -5/8

B. m ≤ -5/8

C. m > -5/8

D. m < -3/8

Xem đáp án

Chọn A

Tam thức : -4x²+ 5x-1 có a= -4 và ∆ = -7< 0

suy ra -4x²+ 5x-1<0 với mọi x

Do đó h(x) luôn dương khi và chỉ khi

f(x) = -x²+ 4( m+1) x+ 1- 4m² luôn âm

Vậy với m< -5/8 thì biểu thức h(x) luôn dương.

Câu 10:

21/07/2024

Cho biểu thức $k (x) = \sqrt{x^{2} - x + m} - 1$

Tìm các giá trị của m để k( x) > 0 với mọi x

A. m > $\frac{5}{4}$

B. m ≥ $\frac{1}{4}$

C. m ≤ $\frac{1}{4}$

D. m > $\frac{3}{4}$

Xem đáp án

Chọn A

Biểu thức k(x) luôn dương

$\Leftrightarrow \sqrt{x^{2} - x + m} - 1 > 0, \forall x \Leftrightarrow \sqrt{x^{2} - x + m} > 1, \forall x \Leftrightarrow x^{2} - x + m > 1, \forall x \Leftrightarrow x^{2} - x + m - 1 > 0, \forall x \Leftrightarrow \{\begin{cases} a = 1 > 0 \\ ∆' = 1 - 4 (m - 1) < 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 > 0 \\ 5 - 4 m < 0 \end{cases} \Leftrightarrow m > \frac{5}{4}$

Vậy với $m > \frac{5}{4}$ thì biểu thức k(x) luôn dương.

Câu 11:

21/07/2024

Cho hàm số:

$y = \frac{mx}{(2 m^{2} + 1) x^{2} - 4 mx + 2}$

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Tồn tại giá trị của m để biểu thức không có nghĩa

B. Hàm số luôn xác định với mọi m

C. Số nguyên nhỏ nhất để hàm số xác định là m=1

D. Tất cả các mệnh đề trên đều sai

Xem đáp án

Chọn B

ĐKXĐ: (2m²+1) x²- 4mx+2 ≠ 0

Xét tam thức bậc hai f(x) = (2m²+1) x²- 4mx+2

Ta có hệ số a= 2m²+1 > 0 và

Δ’ = 4m²-2( 2m²+1) = -2< 0

Suy ra với mọi m ta có f(x) > 0 với mọi x

Vậy tập xác định của hàm số là D= R

Câu 12:

22/07/2024

Cho hàm số

$y = \sqrt{\frac{2 x^{2} - 2 (m + 1) x + m^{2} + 1}{m^{2} x^{2} - 2 mx + m^{2} + 2}}$

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hàm số xác định với mọi m

B. Số nguyên bé nhất mà tại đó hàm số xác định là m= 1

C. Hàm số không xác định với mọi m

D. Tất cả đều đúng

Xem đáp án

Chọn A

ĐKXĐ:

và m²x² – 2mx+ m²+2≠ 0

+Xét tam thức bậc hai :

f(x) = 2x² -2( m+1) x+ m²+1

Ta có hệ số a= 2> 0;

∆ = (m+1) ²- 2( m²+1) = -(m-1) ²≤ 0

Suy ra với mọi m ta có f(x) ≥ 0 với mọi m(1)

+ Xét tam thức bậc hai:

g(x) = m²x² – 2mx+ m²+2

Với m= 0 ta có g(x) = 2> 0

xét với m≠ 0 ta có:

hệ số a= m²> 0

và ∆’ = m²- m²(m²+2) = -m²(m²+1) < 0

Suy ra với mọi m ta có g(x) > 0 với mọi x(2)

Từ (1) và (2) suy ra với mọi m thì

Tìm mệnh đề đúng trong các mệnh đề sau Hàm số xác định với mọi m (ảnh 2)

và m²x² – 2mx+ m²+2≠ 0 đúng với mọi giá trị của x

Vậy tập xác định của hàm số là D = R

Câu 13:

20/07/2024

Tìm m để 3x²- 2( m+1)x - 2m²+ 3m - 2 ≥ 0 với mọi x

A. m < 1

B. m > -1

C. m < -1

D. không có giá trị nào thỏa mãn

Xem đáp án

Chọn D

Để 3x²- 2( m+1) x-2m²+3m-2 ≥ 0 với mọi x khi và chỉ khi:

∆’ = (m+1) ²+ 3( 2m²-3m+2) ≤ 0

Hay 7m²- 7m+7≤ 0 suy ra bpt vô nghiệm

Vậy không có m thỏa mãn yêu cầu bài toán

Câu 14:

22/07/2024

Hàm số

$y = \sqrt{(m + 1) x^{2} - 2 (m - 1) x + 3 m - 3}$ có nghĩa với mọi x

A. m < 1

B. m ≥ 1

C. m ≤ -1

D. m < -1

Xem đáp án

Chọn B

Hàm số có nghĩa với mọi x khi và chỉ khi :

( m+1 ) x²- 2( m-1) x + 3m- 3≥ 0 với mọi x (1)

+ Nếu m= -1 thay vào (1) ta thấy không thỏa mãn

+ Nếu m≠ 1 thì (1) tương đương:

Hàm số y = căn [(m + 1)x^2 - 2(m - 1)x + 3m - 3] có nghĩa với mọi x (ảnh 1)

Câu 15:

17/07/2024

Tìm m để bất phương trình sau luôn đúng với mọi x

$|\frac{x + m}{x^{2} + x + 1}| \leq 1 \forall x \in ℝ$

A. m ≥ 0

B. m ≤ 1

C. 0 ≤ m ≤ 1

D.

Xem đáp án

Chọn C

Ta có: x²+ x+ 1> 0 với mọi x

Để bất phương trình đã cho luôn đúng với mọi x khi và chỉ khi (1) và (2) luôn đúng với x

+ (1) đúng với mọi x khi và chỉ khi 1-m≥0 hay m≤ 1

+ (2) đúng với mọi x khi và chỉ khi ∆’ =- m ≤ 0 hay m≥ 0

Vậy 0≤ m≤ 1 là những giá trị cần tìm

Câu 16:

19/07/2024

Tìm m để mọi x: -1 ≤ x ≤ 1 đều là nghiệm của bất phương trình

3x²-2( m+5) x-m²+2m+ 8 ≤ 0 (1)

A. $m \in (- \infty; - 3] \cup [7; + \infty)$

B. m > -0,5

C. m ≥ 7

D. m ≤ -3

Xem đáp án

Chọn A

Câu 17:

18/07/2024

Cho (m+1) x²- 2(2m-1)x - 4m + 2 < 0. Khẳng định nào sau đây sai?

A.

B.

C.

D.

Xem đáp án

Chọn D

+Với m= -1: bất phương trình trở thành 6x+ 6< 0 hay x< -1

+Với m≠ -1 ta có g(x) =(m+1) x²-2(2m-1) x-4m+2

là tam thức bậc hai có hệ số a= m+1 và ∆ ‘ = 8m²-2m- 1

Bảng xét dấu

Câu 18:

17/07/2024

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm

$\{\begin{cases} x^{2} - 3 x + 2 \leq 0 \\ m x^{2} - 2 (2 m + 1) x + 5 m + 3 \geq 0 \end{cases}$

A. m > -1/2

B. m = -1/2

C. m ≥ -1/2

D. không tồn tại

Xem đáp án

Chọn C

Ta có bất phương trình x²- 3x+ 2≤ 0 khi và chỉ khi 1≤ x≤ 2

Yêu cầu bài toán tương đương với bất phương trình:

mx²-2( 2m+1) x+ 5m+3 $\geq$ 0 (1)

có nghiệm x: 1≤ x≤ 2

+ Ta đi tìm m để bất phương trình (1) vô nghiệm trên S

Tức là bpt f( x) = mx²-2( 2m+1) x+ 5m+3< 0 (2)

đúng với mọi x ∈ S

+ Nếu m= 0 (2) trờ thành: -2x+ 3≤0 hay x> 3/2 nên (2) không đúng với mọi x ∈ S

+ Nếu m≠ 0 tam thức f(x) có hệ số a= m, biệt thức ∆’ = -m²+m+ 1

Bảng xét dấu:

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm m > -1/2 (ảnh 1)

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm m > -1/2 (ảnh 2)

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm m > -1/2 (ảnh 3)

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm m > -1/2 (ảnh 4)

Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm m > -1/2 (ảnh 5)

Câu 19:

23/07/2024

Tìm m để bpt m²x + m( x+1) - 2( x - 1) > 0 nghiệm đúng với mọi x ∈ [-2,1]

A. 0 < m < 3/2

B. m > 0

C. m < 3/2

D. Tìm m để bpt m^2x + m( x+1) - 2( x - 1) > 0 nghiệm đúng với mọi x thuộc [-2,1] (ảnh 2)

Xem đáp án

Chọn A

Câu 20:

23/07/2024

Tìm m để bpt 2x²- (2m+1)x+ m²- 2m + 2 ≤ 0 nghiệm đúng với mọi $x \in [\frac{1}{2}; 2]$

A. $2 \leq m \leq \frac{21 + 2 \sqrt{34}}{10}$

B. $m \leq \frac{21 + 2 \sqrt{34}}{10}$

C. m ≥ 2

D. Tìm m để bpt 2x^2 - (2m+1)x+ m^2 - 2m + 2 nhỏ hơn hoặc bằng 0 nghiệm đúng với mọi x thuộc [1/2; 2] (ảnh 4)

Xem đáp án

Chọn A

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3