24 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Đại số Ôn tập chương 4

Câu 1:

17/06/2026

y = \frac{1}{\sqrt{2 - 3 x}}

là:

A. $(- \infty; \frac{2}{3}]$

B.

(- \infty; \frac{2}{3})

C. $(- \infty; \frac{3}{2}]$

D.

(- \infty; \frac{3}{2})

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Hàm số xác định khi

$2 - 3 x > 0 \Leftrightarrow x < \frac{2}{3}$

Câu 2:

17/06/2026

Tập xác định của hàm số

y = \frac{1}{\sqrt{2 - x}}

là:

A. $(- \infty; 2) .$

B. $(2; + \infty) .$

C. $(- \infty; 2] .$

D. $[2; + \infty) .$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Hàm số xác định khi $2 - x > 0 \Leftrightarrow x < 2$

Câu 3:

17/06/2026

Hệ bất phương trình

\{\begin{cases} (x + 3) (4 - x) > 0 \\ x < m - 1 \end{cases}

vô nghiệm khi

A. $m \leq - 2$

B.

m > - 2

C. $m < - 1$

D.

m = 0

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\{\begin{cases} (x + 3) (4 - x) > 0 \\ x < m - 1 \end{cases} \Leftrightarrow \{\begin{cases} - 3 < x < 4 \\ x < m - 1 \end{cases}$

Hệ bất phương trình vô nghiệm

$m - 1 \leq - 3 \Leftrightarrow m \leq - 2$

Câu 4:

17/06/2026

Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình

\{\begin{cases} 3 (x - 6) < - 3 \\ \frac{5 x + m}{2} > 7 \end{cases}

có nghiệm.

A. $m > - 11$

B.

m \geq - 11

C. $m < - 11$

D.

m \leq - 11

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\{\begin{cases} 3 (x - 6) < - 3 \\ \frac{5 x + m}{2} > 7 \end{cases} \Leftrightarrow \{\begin{cases} 3 x < 15 \\ 5 x + m > 14 \end{cases} \Leftrightarrow \{\begin{cases} x < 5 \\ x > \frac{14 - m}{5} \end{cases}$

Hệ bất phương trình có nghiệm

$\Leftrightarrow \frac{14 - m}{5} < 5 \Leftrightarrow 14 - m < 25 \Leftrightarrow m > - 11$

Câu 5:

17/06/2026

Bất phương trình nào sau đây không tương đương với bất phương trình

x + 5 \geq 0

A. ${(x - 1)}^{2} (x + 5) \geq 0$

B.

- x^{2} (x + 5) \leq 0

C. $\sqrt{x + 5} (x + 5) \geq 0$

D.

\sqrt{x + 5} (x - 5) \geq 0

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

$x + 5 \geq 0 \Leftrightarrow x \geq - 5$

Tập nghiệm của bất phương trình là $T_{1} = [- 5; + \infty)$

$\sqrt{x + 5} (x - 5) \geq 0 \Leftrightarrow \{\begin{cases} x + 5 \geq 0 \\ x - 5 \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq - 5 \\ x \geq 5 \end{cases} \Leftrightarrow x \geq 5$

Tập nghiệm của bất phương trình này là $T_{2} = [5; + \infty)$ .

Vì hai bất phương trình này không có cùng tập nghiệm nên chúng không tương đương nhau.

Câu 6:

17/06/2026

Tập nghiệm của hệ bất phương trình

\{\begin{cases} 3 x + 2 > 2 x + 3 \\ 1 - x > 0 \end{cases}

là:

A. $(\frac{1}{5}; 1)$

B. $(- \infty; - 1)$

C. $(1; + \infty;)$

D. $\emptyset$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Giải từng bất phương trình trong hệ ta có:

$\{\begin{cases} 3 x + 2 > 2 x + 3 \\ 1 - x > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > 1 \\ x < 1 \end{cases}$

Vậy hệ bất phương trình vô nghiệm.

Câu 7:

17/06/2026

Cho nhị thức bậc nhất

f (x) = 23 x - 20

. Khẳng định nào sau đây đúng?

A. $f (x) > 0$ với $\forall x \in ℝ$ .

B. $f (x) > 0$ với

\forall x \in (- \infty; \frac{20}{23})

.

C. $f (x) > 0$ với $x > - \frac{5}{2}$ .

D. $f (x) > 0$ với

\forall x \in (\frac{20}{23}; + \infty)

Xem đáp án

Đáp án: D

Giải thích:

Hướng dẫn giải

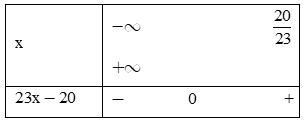
Ta có

$23 x - 20 = 0 \Leftrightarrow x = \frac{20}{23} a = 23 > 0$

Bảng xét dấu

Vậy

f (x) > 0

với

\forall x \in (\frac{20}{23}; + \infty)

Câu 8:

17/06/2026

Các số tự nhiên bé hơn 4 để

f (x) = \frac{2 x}{5} - 23 - (2 x - 16)

luôn âm

A. $\{- 4; - 3; - 2; - 1; 0; 1; 2; 3\}$

B.

- \frac{35}{8} < x < 4

C. $\{0; 1; 2; 3\}$

D. $\{0; 1; 2; - 3\}$

Xem đáp án

Đáp án: C

Giải thích:

Hướng dẫn giải

Ta có

$f (x) = \frac{2 x}{5} - 23 - (2 x - 16) = - \frac{8}{5} x - 7$

$f (x) = 0 \Leftrightarrow x = - \frac{35}{8} a = - \frac{8}{5} < 0$

Bảng xét dấu

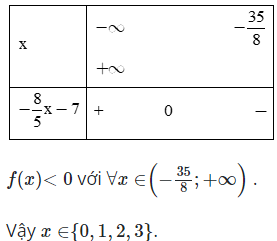
Câu 9:

17/06/2026

Với x thuộc tập hợp nào dưới đây thì

f (x) = 5 x - \frac{x + 1}{5} - 4 - (2 x - 7)

luôn âm

A. $\emptyset$

B. $ℝ$

C. $(- \infty; - 1)$

D.

(- 1; + \infty)

Xem đáp án

Đáp án: C

Giải thích:

Hướng dẫn giải

Ta có

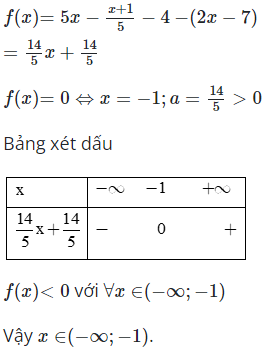
Câu 10:

17/06/2026

Tìm tất cả các giá trị thực của tham số m để

f (x) = m (x - m) - (x - 1)

không âm với mọi

x \in (- \infty; m + 1] .

A. $m = 1$

B.

m > 1

C. $m < 1$

D. $m \geq 1$

Xem đáp án

Đáp án: C

Giải thích:

Hướng dẫn giải

$m (x - m) - (x - 1) \geq 0 \Leftrightarrow (m - 1) x \geq m^{2} - 1$

+ Xét $m = 1 \Rightarrow x \in ℝ$ . (không thỏa)

+ Xét $m > 1$ thì $(1) \Leftrightarrow x \geq m + 1$ không thỏa điều kiện nghiệm đã cho.
+ Xét $m < 1$ thì $(1) \Leftrightarrow x \leq m + 1$ thỏa điều kiện nghiệm đã cho.
Vậy $m < 1$ .

Câu 11:

17/06/2026

Gọi S là tập tất cả các giá trị của x để

f (x) = m x + 6 - 2 x - 3 m

luôn âm khi m <2. Hỏi các tập hợp nào sau đây là phần bù của tập S?

A. $(3; + \infty)$ .

B.

[3; + \infty)

C. $(- \infty; 3)$

D.

(- \infty; 3]

Xem đáp án

Đáp án: D

Giải thích:

Hướng dẫn giải

$m x + 6 - 2 x - 3 m < 0 \Leftrightarrow (2 - m) x > 6 - 3 m \Leftrightarrow x > 3$ (do m <2)

Vậy $S = (3; + \infty) \Rightarrow C_{ℝ} S = (- \infty; 3]$

Câu 12:

17/06/2026

Nghiệm của hệ bất phương trình:

\{\begin{matrix} 2 x^{2} - x - 6 \leq 0 \\ x^{3} + x^{2} - x - 1 \geq 0 \end{matrix}

là:

A. $- 2 \leq x \leq 3$

B.

- 1 \leq x \leq 3

C. $1 \leq x \leq 2$ hoặc $x = - 1$ .

D.

1 \leq x \leq 2

Xem đáp án

Đáp án: C

Giải thích:

Hướng dẫn giải

Ta có

$2 x^{2} - x - 6 \leq 0 \Leftrightarrow - \frac{3}{2} \leq x \leq 2, (I)$

$x^{3} + x^{2} - x - 1 \geq 0 \Leftrightarrow (x + 1) (x^{2} - 1) \geq 0 \Leftrightarrow (x - 1) {(x + 1)}^{2} \geq 0 \Leftrightarrow [\begin{matrix} x = - 1 \\ x \geq 1 \end{matrix} . (I I)$

Từ (I) và (II) suy ra nghiệm của hệ là

$S = [1; 2] \cup \{- 1\}$

Câu 13:

17/06/2026

Bất phương trình:

|x^{4} - 2 x^{2} - 3| \leq x^{2} - 5

có bao nhiêu nghiệm nghiệm nguyên?

A. 0.

B. 1.

C. 2.

D. Nhiều hơn 2 nhưng hữu hạn.

Xem đáp án

Đáp án: A

Giải thích:

Hướng dẫn giải

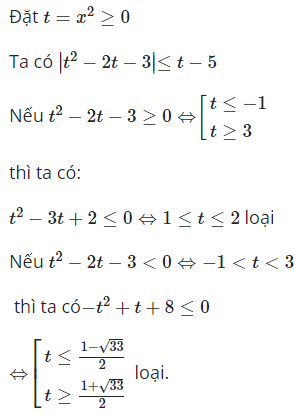
Câu 14:

17/06/2026

Tập nghiệm của hệ bất phương trình

\{\begin{cases} 2 x + 1 > 3 x - 2 \\ - x - 3 \leq 0 \end{cases}

A. $[- 3; + \infty) .$

B. $(- \infty; 3) .$

C. $[- 3; 3) .$

D. $(- \infty; - 3] \cup (3; + \infty) .$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có:

$\{\begin{cases} 2 x + 1 > 3 x - 2 \\ - x - 3 \leq 0 \end{cases} \Leftrightarrow \{\begin{cases} x < 3 \\ x \geq - 3 \end{cases} \Leftrightarrow - 3 \leq x < 3$

Vậy hệ bất phương trình có tập nghiệm là

S = [- 3; 3) .

Câu 15:

17/06/2026

Khẳng định nào sau đây là đúng?

A. $x^{2} \leq 3 x \Leftrightarrow x \leq 3$

B.

\frac{1}{x} < 0 \Leftrightarrow x \leq 1

C. $\frac{x + 1}{x^{2}} \geq 0 \Leftrightarrow x + 1 \geq 0$

D.

x + |x| \geq x \Leftrightarrow |x| \geq 0

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Vì $a \geq b \Leftrightarrow a - c \geq b - c, \forall c \in ℝ$

Trong trường hợp này c=x .

Câu 16:

17/06/2026

Tập nghiệm của bất phương trình:

5 x - \frac{x + 1}{5} - 4 < 2 x - 7

là:

A. $S = \emptyset$

B.

S = ℝ

C. $S = (- \infty; - 1)$

D.

S = (- 1; + \infty)

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

*Giải theo tự luận:

Ta có:

$5 x - \frac{x + 1}{5} - 4 < 2 x - 7$

$\Leftrightarrow 14 x < - 14 \Leftrightarrow x < - 1$

Vậy Tập nghiệm của bất phương trình là: $S = (- \infty; - 1)$

*Giải theo pp trắc nghiệm:

Thay x=-2, thỏa mãn $\Rightarrow$ Loại A, D.

Thay x=0, không thỏa mãn $\Rightarrow$ Loại B. Vậy chọn đáp án C.

Câu 17:

17/06/2026

Tập nghiệm của bất phương trình:

|2 x - 1| \leq x

là

S = [a; b]

. Tính

P = a . b

?

A. $P = \frac{1}{2}$

B.

P = \frac{1}{6}

C. $P = 1$

D.

P = \frac{1}{3}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

*Giải theo tự luận: $|2 x - 1| \leq x$ (1)

TH1: $x < \frac{1}{2}$ , bất phương trình (1) trở thành:

$1 - 2 x \leq x \Leftrightarrow x \geq \frac{1}{3}$

Kết hợp với điều kiện,

ta có: $\frac{1}{3} \leq x < \frac{1}{2}$

TH2: $x \geq \frac{1}{2}$ bất phương trình (1) trở thành:

$2 x - 1 \leq x \Leftrightarrow x \leq 1$

Kết hợp với điều kiện, ta có: $\frac{1}{2} \leq x \leq 1$

Vậy tập nghiệm của bất phương trình là: $S = [\frac{1}{3}; 1] .$ Và $P = \frac{1}{3}$

Câu 18:

17/06/2026

Giá trị nào của thì phương trình

(m - 3) x^{2} + (m + 3) x - (m + 1) = 0

(1) có hai nghiệm phân biệt?

A. $m \in (- \infty; - \frac{3}{5}) \cup (1; + \infty) \ \{3\}$

B.

m \in (- \frac{3}{5}; 1)

C. $m \in (- \frac{3}{5}; + \infty)$

D.

m \in ℝ \ \{3\}

Xem đáp án

Đáp án: A

Giải thích:

Hướng dẫn giải

Ta có (1) có hai nghiệm phân biệt khi

$\{\begin{cases} a \neq 0 \\ Δ' > 0 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 3 \\ 5 m^{2} - 2 m - 3 > 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} m \neq 3 \\ [\begin{array}{l} m < - \frac{5}{3} \\ m > 1 \end{array} \end{cases}$

Câu 19:

17/06/2026

Tìm tập xác định của hàm số

y = \sqrt{2 x^{2} - 5 x + 2}

.

A. $(- \infty; \frac{1}{2}]$

B.

[2; + \infty)

C. $(- \infty; \frac{1}{2}] \cup [2; + \infty)$

D.

[\frac{1}{2}; 2]

Xem đáp án

Đáp án: C

Giải thích:

Hướng dẫn giải

Điều kiện

$2 x^{2} - 5 x + 2 \geq 0 \Leftrightarrow [\begin{array}{l} x \geq 2 \\ x \leq \frac{1}{2} \end{array}$

Vậy tập xác định của hàm số là $(- \infty; \frac{1}{2}] \cup [2; + \infty)$

Câu 20:

17/06/2026

Các giá trị m để tam thức

f (x) = x^{2} - (m + 2) x + 8 m + 1

đổi dấu 2 lần là

A. $m \leq 0$ hoặc $m \geq 28$ .

B. $m < 0$ hoặc

m > 28

.

C. $0 < m < 28$

D.

m > 0

Xem đáp án

Đáp án: B

Giải thích:

Hướng dẫn giải

Để tam thức $f (x) = x^{2} - (m + 2) x + 8 m + 1$ đổi dấu 2 lần khi và chỉ khi

$Δ > 0 \Leftrightarrow {(m + 2)}^{2} - 4 (8 m + 1) > 0 \Leftrightarrow m^{2} - 28 m > 0 \Leftrightarrow [\begin{array}{l} m > 28 \\ m < 0 \end{array}$

Câu 21:

17/06/2026

Cho bất phương trình:

\frac{|x - 1|}{x + 2} > 1

. Nghiệm nguyên lớn nhất của bất phương trình là:

A. -1

B. 1

C. -3

D. 0

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

*Giải theo tự luận: ĐK: $x \neq - 2$

TH1: x < -2, luôn không đúng.

TH2: -2 < x < 1 bất phương trình trở thành:

$1 - x > x + 2 \Leftrightarrow x < - \frac{1}{2}$

Kết hợp với điều kiện,ta có: $- 2 < x < - \frac{1}{2}$

TH3: $x \geq 1$ bất phương trình trở thành: $x - 1 > x + 2$ vô lí.

Vậy bất phương trình có tập nghiệm $S = (- 2; - \frac{1}{2})$

Nghiệm nguyên lớn nhất của bất phương trình là -1

Câu 22:

17/06/2026

Bất phương trình

m x > 3 + m

vô nghiệm khi:

A. $m = 0$

B.

m > 0

C. $m < 0$

D.

m \neq 0

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

*Giải theo tự luận:

Bất phương trình $m x > 3 + m$ vô nghiệm khi:

$\{\begin{cases} m = 0 \\ 3 + m \geq 0 \end{cases} \Leftrightarrow m = 0$

Vậy với $m = 0$ , bất phương trình đã cho vô nghiệm.

*Giải theo pp trắc nghiệm:

Thay $m = 0$ bất phương trình đã cho vô nghiệm. Vậy chọn đáp án A.

Câu 23:

17/06/2026

Tìm m để bất phương trình

m^{2} x + 3 < m x + 4

có nghiệm?

A. $m = 1$

B.

m = 0

C. $m = 0$ và $m = 1$

D.

\forall m \in ℝ

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

*Giải theo tự luận:

$m^{2} x + 3 < m x + 4 \Leftrightarrow m (m - 1) x < 1$

vô nghiệm $\Leftrightarrow \{\begin{cases} m (m - 1) = 0 \\ 1 \leq 0 \end{cases}$ vô lí.

Vậy với $\forall m \in ℝ$ bất phương trình có nghiệm.

Câu 24:

17/06/2026

Điều kiện của m để bất phương trình:

(2 m + 1) x + m - 5 \geq 0

nghiệm đúng với

\forall x \in (0; 1)

:

A. $\frac{- 1}{2} < m \leq 5$

B.

m = 5

C. $m = 5$ và $m = \frac{- 1}{2}$

D.

m \geq 5

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

*Giải theo tự luận:

$(2 m + 1) x + m - 5 \geq 0$

$\Leftrightarrow (2 m + 1) x \geq 5 - m$ (*)

TH1: Với $m > \frac{- 1}{2}$ ,bất phương trình (*) trở thành: $x \geq \frac{5 - m}{2 m + 1}$

Tập nghiệm của bất phương trình là $S = [\frac{5 - m}{2 m + 1}; + \infty)$

Để bất phương trình đã cho nghiệm đúng với $\forall x \in (0; 1)$ thì $(0; 1) \subset [\frac{5 - m}{2 m + 1}; + \infty)$ ,

Hay $\frac{5 - m}{2 m + 1} \leq 0 \Leftrightarrow m \geq 5$

TH2: $m = \frac{- 1}{2}$ ,bất phương trình (*) trở thành: $0 x \geq 5 + \frac{1}{2}$

Bất phương trình vô nghiệm $\Rightarrow$ không có m .

TH3: Với $m < \frac{- 1}{2}$ , bất phương trình (*) trở thành: $x \leq \frac{5 - m}{2 m + 1}$

Tập nghiệm của bất phương trình là $S = (- \infty; \frac{5 - m}{2 m + 1}]$

Để bất phương trình đã cho nghiệm đúng với $\forall x \in (0; 1)$ thì $(0; 1) \subset (- \infty; \frac{5 - m}{2 m + 1}]$ ,

Hay $1 \leq \frac{5 - m}{2 m + 1}$

$\Leftrightarrow 5 - m \leq 2 m + 1 \Leftrightarrow m \geq \frac{4}{3}$

Kết hợp điều kiện $m < \frac{- 1}{2}, \Rightarrow$ không có m thỏa mãn.

Vậy với $m \geq 5$ , bất phương trình đã cho nghiệm đúng với $\forall x \in (0; 1)$ .

*Giải theo trắc nghiệm:

Thay $m = 6$ , bất phương trình trở thành $13 x + 1 \geq 0 \Leftrightarrow x \geq \frac{- 1}{13}$ , bất phương trình nghiệm đúng với $\forall x \in (0; 1)$ $\Rightarrow m = 6$ thỏa mãn.

Vậy chọn D .

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3