50 câu hỏi trắc nghiệm thuộc 15 đề thi THPTQG môn Toán cực hay có lời giải chi tiết (Đề 15)

Hàm số nào sau đây có tập xác định là R :

A. $y = \frac{3 x + 1}{x^{2} + 3 x + 1}$

B. $y = \frac{x^{2}}{x}$

C. $y = \frac{4 x + 2}{x^{2} + 2 x + 3}$

D. $y = \frac{5 x + 1}{x^{2} + 4 x + 4}$

Xem đáp án

Đáp án đúng : C

Câu 2:

Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12

Giới hạn $\lim_{x \to 1} \frac{4 x^{6} - 5 x^{2} + x}{x^{2} - 1}$ bằng $\frac{a}{b}$ (phân số tối giản). Giá trị của A = |a| - 5|b| là:

A. 15

B. 10

C. 5

D. 0

Xem đáp án

Đáp án đúng : B

Câu 3:

01/12/2024

Đồ thị hàm số $y = x^{4} - x^{2} + 1$ có bao nhiêu điểm cực trị có tung độ dương?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án đúng : C

Lời giải

*Phương pháp giải:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.

Bước 3. Lập bảng biến thiên.

Bước 4. Từ bảng biến thiên suy ra các điểm cực trị

*Lý thuyết:

- Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là $- \infty$ ; b là $+ \infty$ ) và điểm x₀ $\in$ (a; b).

a) Nếu tồn tại số h > 0 sao cho f(x) < f(x₀) với mọi x(x₀ – h; x₀ + h) và $x \neq x_{0}$ thì ta nói hàm số f(x) đạt cực đại tại x₀.

b) Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x $\in$ (x₀ – h; x₀ + h) và $x \neq x_{0}$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

- Chú ý:

1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.

Kí hiệu là f_CĐ (f_CT) còn điểm M(x₀; f(x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x₀ thì f’(x₀) = 0.

- Định lí 1

Giả sử hàm số y = f(x) liên tục trên khoảng K = (x₀ – h; x₀ + h) và có đạo hàm trên K hoặc trên K \ {x₀}; với h > 0.

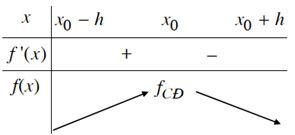
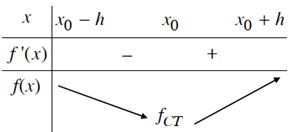
a) Nếu f’(x) > 0 trên khoảng (x₀ – h; x₀) và f’(x) < 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x).

b) Nếu f’(x) < 0 trên khoảng (x₀ – h; x₀) và f’(x) > 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x).

Xem thêm

TOP 40 câu Trắc nghiệm Cực trị hàm số (có đáp án 2024) - Toán 12

Câu 4:

Cho hàm số $y = - \frac{1}{3} m x^{3} + (m - 1) x^{2} - mx + 3$ .Xác định m để: y' = 0 có hai nghiệm phân biệt cùng âm.

A. $m < \frac{1}{2}$

B. $m > 0$

C. $0 < m < \frac{1}{2}$

D. Không tồn tại m.

Xem đáp án

Đáp án đúng : C

Câu 5:

Hàm số $y = x^{3} + 3 x^{2} - 2$ Với các giá trị nào của m thì đồ

thị hàm số cắt đường thẳng d : y = m tại 3 điểm phân

biệt?`

A. $- 2 < m < 0$

B. $0 < m < 2$

C. $- 2 < m < 2$

D. $m < - 2 \lor m > 2$

Xem đáp án

Đáp án đúng : C

Câu 6:

Tìm hệ số của $x^{5}$ trong khai triển biểu thức

$P = x {(1 - 2 x)}^{n} + x^{2} {(1 + 3 x)}^{2 x}$ . Biết rằng $A_{n}^{2} - C_{n + 1}^{n - 1} = 5$

A. 3240

B. 3320

C. 3210

D. 3340

Xem đáp án

Đáp án đúng : B

Câu 7:

Trong cuộc thi “ Rung chuông vàng”, đội Thủ Đức có 20 bạn lọt vào vòng chung kết, trong đó có 5 bạn nữ và 15 bạn nam. Để sắp xếp vị trí chơi, ban tổ chức chia các bạn thành 4 nhóm A, B, C, D, mỗi nhóm có 5 bạn. Việc chia nhóm được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 5 bạn nữ thuộc cùng một nhóm gần nhất với:

A. $0, 26 . 10^{- 3}$

B. $0, 52 . 10^{- 3}$

C. $0, 37 . 10^{- 3}$

D. $0, 41 . 10^{- 3}$

Xem đáp án

Đáp án đúng : A

Câu 8:

Với các giá trị nào của m thì đồ thị hàm số $y = \frac{2 x^{2} - 3 x + m}{x - m}$ không có tiệm cận đứng?

A. m = 0

D. m = 1

Xem đáp án

Đáp án đúng : C

Câu 9:

Cho hàm số (C).Cho các mệnh đề :

(1) Hàm số có tập xác định R

(2) Hàm số đạt cực trị tại

(3) Hàm số đồng biến trên các khoảng

(4) Điểm là điểm cực tiểu

(5)

Hỏi bao nhiêu mệnh đề đúng?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án đúng : C

Câu 10:

Cho mệnh đề:

1) Mặt cầu có tâm $I (1; 0; - 1)$ , đường kính bằng 8 là: ${(x - 1)}^{2} + y^{2} + {(z + 1)}^{2} = 16$

2) Mặt cầu có đường kính AB với $A (- 1; 2; 1)$ , $B (0; 2; 3)$ là: ${(x + \frac{1}{2})}^{2} + {(y - 2)}^{2} + {(z - 2)}^{2} = \sqrt{\frac{5}{4}}$

3) Mặt cầu có tâm $O (0; 0; 0)$ và tiếp xúc với mặt cầu (S) có tâm $(3; - 2; 4)$ , bán

kính bằng 1 là:

Số mệnh đề đúng là bao nhiêu:

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án đúng : B

Câu 11:

Công ty mỹ phẩm MILANO vừa cho ra mắt sản phẩm mới là chiếc thỏi son

mang tên Lastug có dạng hình trụ (Như hình) có chiều cao h (cm), bán kính

đáy r (cm), thể tích yêu cầu là $20, 25 π$ ( $c m^{3}$ ) mỗi thỏi.

Biết rằng chi phí sản xuất cho mỗi thỏi son như vậy được xác đinh theo công

thức: $T = 60000 r^{2} + 20000 r h$ (đồng)

Để chi phí sản xuất là thấp nhất thì tổng (r + h) bằng bao nhiêu?

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án đúng : B

Câu 12:

Giá trị của $\frac{\sqrt[5]{81} . \sqrt[5]{3} . \sqrt[5]{9} . \sqrt{12}}{{(\sqrt[3]{\sqrt{3}})}^{2} . \sqrt{18} . \sqrt[5]{27} . \sqrt{6}}$ là:

A. $3^{- \frac{8}{15}}$

B. $3^{\frac{8}{15}}$

C. $3^{- \frac{15}{8}}$

D. $3^{\frac{15}{8}}$

Xem đáp án

Đáp án đúng : A

Câu 13:

23/07/2024

Tìm giá trị của x để hàm số có nghĩa: $y = \frac{1}{\sqrt{\log_{\frac{1}{5}} 3} - \log_{\sqrt{5}} x + \log_{5} (x + 2)}$

A. $0 < x < 1$

B. $x > - 1$

C. $x < 0$

D. $x > 1$

Xem đáp án

Đáp án đúng : A

Câu 14:

Cho phương trình: $2 P_{n} + 6 A_{n}^{2} - P_{n} A_{n}^{2} = 12$ . Biết phương trình trên có 2 nghiệm là a, b. Giá trị của S = ab(a + b) là

A. 30

B. 84

C. 20

D. 162

Xem đáp án

Đáp án đúng : A

Câu 15:

Có kết luận gì về a nếu ${(2 a + 1)}^{- 3} > {(2 a + 1)}^{- 1} (1)$

A. $a \in (- \infty; - 1) \cup (- \frac{1}{2}; 0)$

B. $a \in (- \infty; - 1) \cup (0; \frac{1}{2})$

C. $a \in (- \infty; - 1) \cup (- \frac{1}{6}; 0)$

D. $a \in (- \infty; - 2) \cup (- 1; 0)$

Xem đáp án

Đáp án đúng : A

Câu 16:

23/07/2024

Đạo hàm của hàm số $y = \ln (\sqrt{2 x - 6} - 1)$ là:

A. $y' = \frac{1}{\sqrt{2 x - 6} (\sqrt{2 x - 6} - 1)}$

B. $y' = - \frac{1}{2 \sqrt{2 x - 6} (\sqrt{2 x - 6} - 1)}$

C. $y' = \frac{1}{2 \sqrt{2 x - 6} (\sqrt{2 x - 6} - 1)}$

D. $y' = \frac{1}{\sqrt{2 x - 6} (\sqrt{2 x - 6} - 1)}$

Xem đáp án

Đáp án đúng : D

Câu 17:

Phương trình $2^{x - 1} - 2^{x^{2} - x} = {(x - 1)}^{2}$ có bao nhiêu nghiệm?

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Đáp án đúng : D

Câu 18:

Xét hệ phương trình $\{\begin{cases} \log_{x} (3 x + 2 y) = 2 \\ \log_{y} (2 x + 3 y) = 2 \end{cases} (I)$ có nghiệm (x;y). Khi đó phát biểu nào sau đây đúng:

A. $x + 2 y = 0$

B. $x - 2 y = 4$

C. $x - y = 0$

D. $x + y = 0$

Xem đáp án

Đáp án đúng : C

Câu 19:

$\frac{\sin^{4} x + \cos^{4} x}{\sin 2 x} = \frac{1}{2}$ $(\tan x + c o t x)$ . Nghiệm thuộc khoảng [0;1] là:

A. $\emptyset$

B. $\frac{3 π}{8}$

C. $\frac{π}{12}$

D. $\frac{π}{8}$

Xem đáp án

Đáp án đúng : A

Câu 20:

21/07/2024

Tập nghiệm của phương trình $- 9 \sin x + 6 \cos x - 3 \sin 2 x + \cos 2 x = - 10$ là: $x = \frac{aπ}{b} + k 2 π (k \in ℤ)$ tính giá trị của $a^{2} - b$ : (biết a, b tối giản)

A. 3

B. - 2

C.4

D. - 1

Xem đáp án

Đáp án đúng : D

Câu 21:

21/07/2024

Cho tích phân $I = \int_{0}^{1} \frac{3 x + 3 \ln (3 x + 1)}{{(x + 1)}^{2}} d x$ = $= \int_{0}^{1} (\frac{a}{3 x +!} - \frac{b}{x + 1}) d x$ .Tính

$A = a^{2} - b^{2}$ . Chọn đáp án đúng:

A. 0

B. 2

C. 3

D. 4

Xem đáp án

Đáp án đúng : A

Câu 22:

Tính nguyên hàm $I = \int (x - 2) \sin 3 x d x$ $= - \frac{(x - 2) \cos 3 x}{a} + b \sin 3 x$ Tính . Chọn đáp án

đúng:

A. 6

B. 14

C. 34

D. 22

Xem đáp án

Đáp án đúng : A

Câu 23:

Nguyên hàm của $f (x) = (x - 2) (x^{2} + 2 x + 4)$ là:

A. $\frac{x^{4}}{4} - 8 x + C$

B. $x^{4} - 8 x + C$

C. $\frac{x^{4}}{4} - 4 x + C$

D. $\frac{x^{4}}{4} - 8 x$

Xem đáp án

Đáp án đúng : A

Câu 24:

Cho hàm $f (x) = \frac{(x + 2^{2})}{x^{3}}$ có nguyên hàm là hàm F(x). Biết F(1)=6. Khi đó F(x) có dạng:

A. $\ln |x| - \frac{4}{x} - \frac{2}{x^{2}} + 6$

B. $\ln |x| + \frac{4}{x} - \frac{2}{x^{2}} + 4$

C. $\ln |x| + \frac{4}{x} - \frac{2}{x^{2}} + 4$

D. $\ln |x| - \frac{4}{x} - \frac{2}{x^{2}} + 6$

Xem đáp án

Đáp án đúng : A

Câu 25:

Một vật chuyển động chậm dần với vận tốc $v = 120 - 12 t (m / s)$ .Hỏi rằng trong 2s trước khi dừng hẳn vật di chuyển được bao nhiêu mét?

A. 28 m

B. 35 m

C. 24 m

D. 38 m

Xem đáp án

Đáp án đúng : C

Câu 26:

Cho $a \in (0; \frac{π}{2}]$ và thỏa mãn $c o s α (2 \sin^{2} α + \sin α - 3) = 0$ . Tính giá trị của $c o t \frac{α}{2}$

A. $\frac{1}{2}$

B. $\frac{3}{2}$

C. 4

D. 1

Xem đáp án

Đáp án đúng : D

Câu 27:

Tìm GTLN và GTNN của hàm số $c o s α (2 \sin^{2} α + \sin α - 3) = 0$ là:

A. $\{\begin{cases} m a x y = 1 \\ m i n y = \frac{- 1}{11} \end{cases}$

B. $\{\begin{cases} m a x y = 2 \\ m i n y = \frac{- 2}{11} \end{cases}$

C. $\{\begin{cases} m a x y = 2 \\ m i n y = \frac{2}{11} \end{cases}$

D. $\{\begin{cases} m a x y = 1 \\ m i n y = \frac{1}{11} \end{cases}$

Xem đáp án

Đáp án đúng : C

Câu 28:

22/07/2024

Trong mặt phẳng oxy M,N,P là tọa độ điểm biểu diễn của số phức $z_{1} = - 5 + 6 i, z_{2} = - 4 - i; z_{3} = 4 + 3 i$

Tọa độ trực tâm H của tam giác MNP là:

A. $(3; 1)$

B. $(- 1; 3)$

C. $(2; - 3)$

D. $(- 3; 2)$

Xem đáp án

Đáp án đúng : D

Câu 29:

18/07/2024

Cho $a \in (0; \frac{π}{2}]$ và thỏa mãn $c o s α (2 \sin^{2} α + \sin α - 3) = 0$ . Tính giá trị của $c o t \frac{α}{2}$

A. y = sin2x

B. y = 2cosx + 3

C. y = sinx + cosx

D. y = tan2x + cotx

Xem đáp án

Đáp án đúng : B

Câu 30:

Cho hình chóp S.ABC có SA vuông góc với (ABC), hai mặt phẳng (SAB), và (SBC), vuông góc với nhau, SB=3, $\hat{B S C} = 30^{°}, \hat{A S B} = 60^{°}$ . Thể tích khối chóp S.ABC là:

A. $\frac{9}{8}$

B. 3

C. 12

D. 6

Xem đáp án

Đáp án đúng : A

Câu 31:

16/07/2024

Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có AB = 2AD = 2CD, SA vuông góc với đáy (ABCD). Góc giữa SC và đáy bằng $60^{°}$ . Biết khoảng cách từ B đến (SCD) là $\frac{a \sqrt{42}}{7}$ , khi đó tỉ số $\frac{V_{S . A B C D}}{a^{3}}$ bằng

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{6}}{3}$

C. $\frac{\sqrt{6}}{2}$

D. $\frac{\sqrt{3}}{3}$

Xem đáp án

Đáp án đúng : C

Câu 32:

18/07/2024

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa SB và AD bằng:

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a \sqrt{3}}{3}$

C. $\frac{a \sqrt{4}}{4}$

D. $\frac{a \sqrt{3}}{6}$

Xem đáp án

Đáp án đúng : B

Câu 33:

Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC = $\sqrt{3} a$ , SA = $\sqrt{2} a$ và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:

A. $a \sqrt{5}$

B. $\frac{a \sqrt{5}}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $\frac{a \sqrt{6}}{2}$

Xem đáp án

Đáp án đúng : B

Câu 34:

Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc 30⁰. Biết hình chiếu vuông góc của A’ trên trùng với trung điểm cạnh BC. Tính bán kính mặt cầu ngoại tiếp tứ diện A’ABC.

A. $a \sqrt{3}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{3}}{3}$

Xem đáp án

Đáp án đúng : D

Câu 35:

Diện tích và chu vi của một hình chữ nhật ABCD (AB > AD) theo thứ tự là $2 a^{2}$ và $6 a$ . Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này.

A. $2 {πa}^{3}; 4 {πa}^{2}$

B. $4 {πa}^{3}; 4 {πa}^{2}$

C. $2 {πa}^{3}; 2 {πa}^{2}$

D. $4 {πa}^{3}; 2 {πa}^{2}$

Xem đáp án

Đáp án đúng : A

Câu 36:

17/07/2024

Một chiếc cốc dạng hình nón chứa đầy rượu. Trương Phi uống một lượng rượu nên “chiều cao” của rượu còn lại trong cốc bằng một nửa chiều cao ban đầu. Hỏi Trương Phi đã uống bao nhiêu phần rượu trong cốc ?

A. $\frac{1}{12}$

B. $\frac{7}{8}$

C. $\frac{1}{4}$

D. $\frac{1}{6}$

Xem đáp án

Đáp án đúng : B

Câu 37:

18/07/2024

Trong không gian Oxyz cho hai điểm $M (2; - 1; 7)$ , $N (4; 5; - 2)$ . Đường thẳng MN cắt mặt phẳng (Oyz) tại P. Tọa độ điểm P là:

A. $(0; - 7; 16)$

B. $(0; 7; - 16)$

C. $(0; - 5; 12)$

D. $(0; 5; - 12)$

Xem đáp án

Đáp án đúng : A

Câu 38:

21/07/2024

Trong không gian Oxyz, phương trình mặt phẳng $(α)$ cắt ba trục tọa độ tại $M (- 3; 0; 0)$ , $N (0; 4; 0)$ , $P (0; 0; - 2)$ có phương trình là:

A. $4 x - 3 y + 6 z + 12 = 0$

B. $4 x - 3 y + 6 z - 12 = 0$

C. $4 x + 3 y + 6 z + 12 = 0$

D. $4 x + 3 y - 6 z + 12 = 0$

Xem đáp án

Đáp án đúng : A

Câu 39:

Trong không gian Oxyz cho hai vectơ $\overset{⇀}{a} = (3; - 2; 1)$ , $\overset{⇀}{b} = (2; 1; - 1)$ . Với giá trị nào của m thì hai vectơ $\overset{⇀}{u} = m \overset{⇀}{a} - 3 \overset{⇀}{b}$ và $\overset{⇀}{v} = 3 \overset{⇀}{a} - 2 m \overset{⇀}{b}$ cùng phương?

A. $m = \pm \frac{2 \sqrt{3}}{3}$

B. $m = \pm \frac{3 \sqrt{2}}{2}$

C. $m = \pm \frac{3 \sqrt{5}}{5}$

D. $m = \pm \frac{5 \sqrt{7}}{7}$

Xem đáp án

Đáp án đúng : B

Câu 40:

Trong không gian Oxyz cho tam giác MNP với $M (1; 0; 0)$ , $N (0; 0; 1)$ , $P (2; 1; 1)$ . Góc M của tam giác MNP bằng:

A. $45^{°}$

B. $60^{°}$

C. $90^{°}$

D. $120^{°}$

Xem đáp án

Đáp án đúng : C

Câu 41:

Xét các hình chóp S.ABC có SA = SB = SC = AB = BC = a. Giá trị lớn nhất của thể tích hình chóp S.ABC bằng:

A. $\frac{a^{3}}{12}$

B. $\frac{a^{3}}{8}$

C. $\frac{a^{3}}{4}$

D. $\frac{3 \sqrt{3} a^{3}}{4}$

Xem đáp án

Đáp án đúng : B

Câu 42:

Đường thẳng (d) vuông góc với $m p (P) : x + y + z + 1 = 0$ và cắt cả 2 đường thẳng $\frac{x - 1}{2} = \frac{y + 1}{- 1} = z$ và $(d_{2}) : \{\begin{cases} x - 2 y + z - 1 = 0 \\ 2 x - y - 2 z + 1 = 0 \end{cases}$ có phương trình là:

A. $\{\begin{cases} 2 x + y - 3 z + 1 = 0 \\ x - 2 y + z = 0 \end{cases}$

B. $\{\begin{cases} 2 x + y - 3 z - 1 = 0 \\ x - 2 y + z - 1 = 0 \end{cases}$

C. $\{\begin{cases} x + y - 3 z - 1 = 0 \\ 2 x - 2 y + z - 1 = 0 \end{cases}$

D. $\{\begin{cases} x + y - 3 z + 1 = 0 \\ 2 x - 2 y + z = 0 \end{cases}$

Xem đáp án

Đáp án đúng : B

Câu 43:

16/07/2024

Đường thẳng đi qua $I (- 1; 2; 3)$ cắt hai đường thẳng $(d) : \frac{x - 1}{3} = \frac{y + 1}{1} = \frac{z}{1}$ và $(d') : \frac{x - 2}{2} = \frac{y + 1}{3} = \frac{z + 1}{- 5}$ là:

Xem đáp án

Đáp án đúng : C

Câu 44:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng $(P) : 5 x - 2 y + 5 z - 1 = 0$ và $(Q) : x - 4 y - 8 z + 12 = 0$ .Mặt phẳng (R) đi qua điểm M trùng với gốc tọa độ O, vuông góc với mặt phẳng (P) và tạo với mặt phẳng (Q) một góc $α = 45^{°}$ . Biết $(R) : x + 20 y + c z + d = 0$ Tính S = cd

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án đúng : D

Câu 45:

23/07/2024

Trong không gian Oxyz, cho các điểm $A (2; 3; 0)$ , $B (0; - \sqrt{2}; 0)$ và đường thẳng d có phương trình $\{\begin{cases} x = t \\ y = 0 \\ z = 2 - t \end{cases}$ . Điểm $C (a; b; c)$ trên đường thẳng d sao cho tam giác ABC có chu vi nhỏ nhất. Nhận định nào sau đây sai?

A. a + c là một số nguyên dương

B.a - c là một số âm

C. a + b + c = 2

D.abc = 0

Xem đáp án

Đáp án đúng : B

Câu 46:

Trong không gian hệ trục tọa độ , cho 3 điểm $A (- 2; 2; 3)$ ; $B (1; - 1; 3)$ ; $C (3; 1; - 1)$ và mặt phẳng $(P) : x + 2 z - 8 = 0$ . Gọi M là điểm thuộc mặt phẳng (P) sao cho giá trị của biểu thức $T = 2 M A^{2} + M B^{2} + 3 M C^{2}$ nhỏ nhất. Tính khoảng cách từ điểm M đến mặt phẳng $(Q) : - x + 2 y - 2 z - 6 = 0$

A. 4

B. 2

C. $\frac{4}{3}$

D. $\frac{2}{3}$

Xem đáp án

Đáp án đúng : A

Câu 47:

Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] là một đường gấp khúc như hình vẽ bên. Tính tích phân $I = \int_{- 1}^{4} f (x) d x$

A. $I = \frac{5}{2}$

B. $I = 3$

C. $I = \frac{11}{2}$

D. $I = 5$

Xem đáp án

Đáp án đúng : A

Câu 48:

Một người gửi 10 triệu đồng vào ngân hàng trong thời gian 10 năm với lãi suất 5% một năm. Hỏi rằng người đó nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lãi suất $\frac{5}{12}$ % một tháng.

A. Nhiều hơn 181148,71 đồng

B. Ít hơn 181148,71 đồng

C. Bằng nhau

D. Ít hơn 191148,61 đồng

Xem đáp án

Đáp án đúng : A

Câu 49:

Cho số phức $z = x + y i$ với x, y là các số thực không âm thỏa mãn $|\frac{z - 3}{z - 1 + 2 i}|$ và biểu thức $P = |z^{2} - z^{- 2}| + i (z^{2} - z^{- 2})$

$[z (1 - i) + \bar{z} (1 + i)]$ . Giá trị lớn nhất và giá trị

nhỏ nhất của P lần lượt là:

A. 0 và - 1

B. 3 và - 1

C. 3 và 0

D. 2 và 0

Xem đáp án

Đáp án đúng : A

Câu 50: