Câu hỏi:
01/12/2024 84Đồ thị hàm số có bao nhiêu điểm cực trị có tung độ dương?
A. 1
B. 2
C. 3
D. 4
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng : C
Lời giải
*Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị
*Lý thuyết:
- Định nghĩa.
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là ; b là ) và điểm x0(a; b).
a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực đại tại x0.
b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực tiểu tại x0.
- Chú ý:
1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.
Kí hiệu là fCĐ (fCT) còn điểm M(x0; f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x0 thì f’(x0) = 0.
- Định lí 1
Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0 – h; x0 + h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.
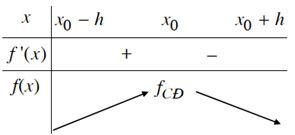
a) Nếu f’(x) > 0 trên khoảng (x0 – h; x0) và f’(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
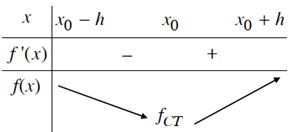
b) Nếu f’(x) < 0 trên khoảng (x0 – h; x0) và f’(x) > 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] là một đường gấp khúc như hình vẽ bên. Tính tích phân
Câu 4:
Trong cuộc thi “ Rung chuông vàng”, đội Thủ Đức có 20 bạn lọt vào vòng chung kết, trong đó có 5 bạn nữ và 15 bạn nam. Để sắp xếp vị trí chơi, ban tổ chức chia các bạn thành 4 nhóm A, B, C, D, mỗi nhóm có 5 bạn. Việc chia nhóm được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 5 bạn nữ thuộc cùng một nhóm gần nhất với:
Câu 5:
Cho hình chóp S.ABC có SA vuông góc với (ABC), hai mặt phẳng (SAB), và (SBC), vuông góc với nhau, SB=3, . Thể tích khối chóp S.ABC là:
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa SB và AD bằng:
Câu 7:
Cho phương trình:. Biết phương trình trên có 2 nghiệm là a, b. Giá trị của S = ab(a + b) là
Câu 8:
Xét hệ phương trình có nghiệm (x;y). Khi đó phát biểu nào sau đây đúng:
Câu 9:
Trong không gian Oxyz cho hai vectơ ,. Với giá trị nào của m thì hai vectơ và cùng phương?
Câu 11:
Xét các hình chóp S.ABC có SA = SB = SC = AB = BC = a. Giá trị lớn nhất của thể tích hình chóp S.ABC bằng:
Câu 12:
Cho hàm số .Xác định m để: y' = 0 có hai nghiệm phân biệt cùng âm.
Câu 14:
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại A có BC =, SA = và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
Câu 15:
Cho hàm số (C).Cho các mệnh đề :
(1) Hàm số có tập xác định R
(2) Hàm số đạt cực trị tại
(3) Hàm số đồng biến trên các khoảng
(4) Điểm là điểm cực tiểu
(5)
Hỏi bao nhiêu mệnh đề đúng?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)