20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Vecto trong không gian cơ bản (P1) (Đề số 5)

Câu 1:

22/07/2024

Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:

A.D( -8; 5)

B. D(- 12; - 5)

C.D(12; 5)

D. Đáp án khác .

Xem đáp án

Ta có: tứ giác ABCD là hình bình hành khi : $\vec{A B} = \vec{D C}$

mà $\vec{A B} (7; - 4); \vec{D C} (- 5 - x; 1 - y)$

$\Rightarrow \{\begin{cases} - 5 - x = 7 \\ 1 - y = - 4 \end{cases} \Leftrightarrow \{\begin{cases} x = - 12 \\ y = 5 \end{cases} \Rightarrow D (- 12; 5)$

Câu 2:

17/07/2024

Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?

A.

B.

C.

D.

Xem đáp án

Câu 3:

18/07/2024

Cộng các vectơ có cùng độ dài 5 và cùng giá. Khẳng định nào sau đây đúng?

A. Cộng 5 vectơ ta được kết quả là $\vec{0}$

B. Cộng 6 vectơ đôi một ngược hướng ta được kết quả là $\vec{0}$

C. Cộng 121 vectơ ta được kết quả là $\vec{0}$

D. Cộng 25 vectơ ta được vectơ có độ dài là 0.

Xem đáp án

Cộng số chẵn các vectơ đôi một ngược hướng cùng độ dài ta được vectơ $\vec{0}$ .

Chọn B.

Câu 4:

17/07/2024

Cho tứ giác ABCD. Điều kiện cần và đủ để $\vec{A B} = \vec{C D}$ ?

A. ABCD là hình bình hành

B. ABDC là hình bình hành.

C. AD và BC có cùng trung điểm

D. AB= CD

Xem đáp án

Câu 5:

12/10/2024

Cho tứ giác ABCD. Gọi M; N; P; Q lần lượt là trung điểm của AB; BC; CD ; DA. Khẳng định nào sai.

A.

B.

C. $\vec{M Q} = \vec{N P}$

D.

Xem đáp án

Đáp án đúng là: D

*Phương pháp giải:

Sử dụng định nghĩa vecto, hai vecto cùng phương, hai vecto bằng nhau.

*Lời giải:

+ Xét tam giác ABC có M; N lần lượt là trung điểm của AB; BC

nên MN là đường trung bình của tam giác ABC.

$\Rightarrow M N / / A C; M N = \frac{1}{2} A C$ (1)

+ Tương tự ta có: $P Q / / A C; P Q = \frac{1}{2} A C$ (2)

Từ (1) và (2) suy ra: MN = PQ và MN// PQ

Do đó, tứ giác MNPQ là hình bình hành.

* Một số lý thuyết liên quan:

Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.

Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu : $\vec{A B}$

Vectơ còn được kí hiệu là: $\vec{a}, \vec{b}, \vec{x}, \vec{y}, ...$

Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là $\vec{0}$

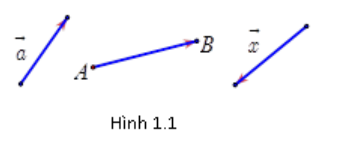
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ

- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương

- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.

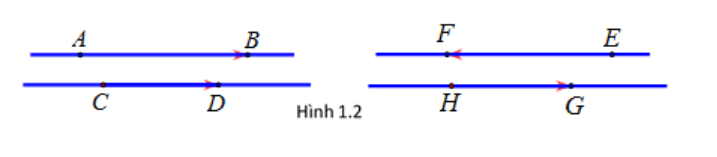
Ví dụ: Ở hình vẽ trên trên (hình 2) thì hai vectơ $\vec{A B}$ và $\vec{C D}$ cùng hướng còn $\vec{E F}$ và $\vec{H G}$ ngược hướng.

Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.

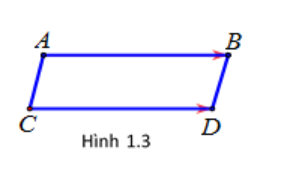
- Độ dài đoạn thẳng $A B$ gọi là độ dài véc tơ $\vec{A B}$ , kí hiệu $|\vec{A B}|$ .

Vậy $|\vec{A B}| = A B$ .

- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Toán 10 CTST Bài 1: Xác định vectơ. Tìm điểm đầu, điểm cuối, giá của vectơ có đáp án

Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu)

100 câu trắc nghiệm Vecto trong không gian cơ bản (P1)

Câu 6:

22/07/2024

Cho tam giác ABC vuông cân đỉnh A, đường cao AH. Khẳng định nào sau đây sai?

A.

B.

C.

D.

Xem đáp án

Do Tam giác ABC cân tại A, AH là đường cao nên H là trung điểm BC.

+Đáp án A. Ta có

Câu 7:

17/07/2024

Cho hình thoi ABCD cạnh a và góc $\hat{B A D}$ = $60^{o}$ Đẳng thức nào sau đây đúng?

A. $\vec{A B} = \vec{A D}$

B. $|\vec{B D}| = a$

C. $\vec{B D} = \vec{A C}$

D. $\vec{B C} = \vec{D A}$

Xem đáp án

Từ giả thiết ta có tam giác ABD cân tại A và có 1 góc bằng 60.

suy ra tam giác ABD đều cạnh a nên

Câu 8:

19/07/2024

Cho 2 điểm phân biệt A; B và 1 điểm C. Có bao nhiêu điểm D thỏa mãn $|\vec{A B}| = |\vec{C D}|$

A. 0

B. 1

C. 10

D. vô số

Xem đáp án

Ta có $|\vec{A B}| = |\vec{C D}|$

khi và chỉ khi AB= CD

Suy ra tập hợp các điểm D thỏa yêu cầu bài toán là đường tròn tâm C bán kính AB.

Chọn D

Câu 9:

17/07/2024

Cho tam giác ABC có M thỏa mãn điều kiện

$\vec{M A} + \vec{M B} + \vec{M C} = \vec{0}$ Xác định vị trí điểm M

A. M là điểm thứ tư của hình bình hành ACBM

B.M là trung điểm của đoạn thẳng AB

C.M trùng C

D.M là trọng tâm tam giác ABC

Xem đáp án

Gọi G là trọng tâm tam giác ABC.

Ta có: $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Mà $\vec{M A} + \vec{M B} + \vec{M C} = \vec{0} \Rightarrow \vec{M G} = \vec{0}$

Do đó, hai điểm M và G trùng với nhau

Chọn D.

Câu 10:

17/07/2024

Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $|\vec{M B} - \vec{M C}| = |\vec{B M} - \vec{B A}|$ là?

A. đường thẳng AB

B. trung trực đoạn BC

C. đường tròn tâm A: bán kính BC

D. đường thẳng qua A và song song với BC

Xem đáp án

Ta có

Mà A; B; C cố định nên tập hợp điểm M là đường tròn tâm A, bán kính BC.

Chọn C

Câu 11:

19/07/2024

Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn $\vec{M A} + \vec{M B} - \vec{M C} = \vec{M D}$

A. một đường tròn.

B. một đường thẳng.

C. tập rỗng.

D. một đoạn thẳng.

Xem đáp án

Không có điểm M thỏa mãn.

Chọn C

Câu 12:

19/07/2024

Gọi O là tâm của hình vuôn ABCD. Vectơ nào trong các vectơ dưới đây bằng $\vec{C A}$ ?

A.

B.

C.

D.

Xem đáp án

Câu 13:

23/07/2024

Cho tam giác ABC và điểm M thỏa mãn $\vec{M B} + \vec{M C} = \vec{A B}$ Tìm vị trí điểm M.

A. M là trung điểm của AC

B.M là trung điểm của AB

C.M là trung điểm của BC

D.M là điểm thứ tư của hình bình hành ABCM

Xem đáp án

Gọi I là trung điểm của BC

Chọn A

Câu 14:

18/07/2024

Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB; CD. Biểu diễn $\vec{M N}$ theo hai vecto $\vec{A D}; \vec{B C}$

A. $\vec{M N} = \frac{1}{2} (\vec{A D} + \vec{B C})$

B. $\vec{M N} = \vec{A D} + \vec{B C}$

C. $\vec{M N} = \frac{1}{2} (\vec{D A} - \vec{B C})$

D. $\vec{M N} = \frac{1}{2} \vec{A D} + \vec{B C}$

Xem đáp án

Chọn A.

Ta có: $\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$ (1)

$\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N}$ (2)

Lấy (1) + (2) ta được:

$2 \vec{M N} = (\vec{M A} + \vec{M B}) + (\vec{A D} + \vec{B C}) + (\vec{D N} + \vec{C N}) = \vec{A D} + \vec{B C} \Rightarrow \vec{M N} = \frac{1}{2} (\vec{A D} + \vec{B C})$

Câu 15:

22/07/2024

Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$