Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 23 Tập 2 Chân trời sáng tạo

    Với Giải SBT Toán 10 trang 23 Tập 2 trong Bài tập cuối chương 7 Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 23.

    1 759 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 23 Tập 2 Chân trời sáng tạo

    Bài 9 trang 23 SBT Toán 10 Tập 2: Một người phát cầu qua lưới từ độ cao y0 mét, nghiêng một góc α so với phương ngang với vận tốc đầu v0.

    Phương trình chuyển động của quả cầu là:

    y=−g2v02cos2αx2+tanαx+y0 với g = 10 m/s2

    Viết phương trình chuyển động của quả cầu nếu α=450,y0=0,3m và v0 = 7,67 m/s.

    b) Để cầu qua được lưới bóng cao 1,5 m thì người phát cầu phải đứng cách lưới bao xa?

    Lưu ý: Đáp số làm tròn đến hàng phần trăm.

    Lời giải:

    a) Ta có

    y=−g2v02cos2αx2+tanαx+y0

    Thay α=450,y0=0,3 và v0 = 7,67 vào phương trình trên ta được:

    y = −102.7,672.cos245° + tan45°.x + 0,3 hay y = –0,17x2 + x + 0,3.

    b) Với x là khoảng cách từ người phát cầu đến lưới thì cầu phát được qua lưới khi và chỉ khi y ( x ) > 1,5 hay –0,17x2 + x + 0,3 > 1,5 hay –0,17x2 + x – 1,2 > 0.

    Xét tam thức bậc hai f(x) = – 0,17x2 + x – 1,2 có ∆ = 12 – 4.(– 0,17).(– 1,2) = 0,184 > 0 nên f(x) có hai nghiệm phân biệt x1 ≈ 4,20 và x2 ≈ 1,68.

    Ta có a = – 0,17 < 0 suy ra f(x) > 0 khi 1,68 < x < 4,20.

    Vậy người phát cầu cần đứng cách lưới trong khoảng từ 1,68 m đến 4,20 m.

    Bài 10 trang 23 SBT Toán 10 Tập 2: Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD = 6.

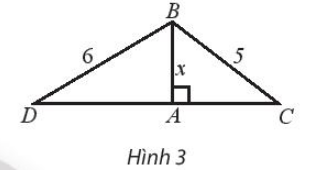
    Sách bài tập Toán 10 Bài tập cuối chương 7 - Chân trời sáng tạo (ảnh 1)

    a) Biểu diễn độ dài cạnh AC và AD theo x.

    b) Tìm x để chu vi của tam giác ABC là 12.

    c) Tìm x để AD = 2AC

    Lời giải:

    a) Vì x là khoảng cách AB nên x > 0

    Áp dụng định lí Phytagoras cho tam giác ABC:

    AB2 + AC2 = BC2

    ⇒ AC2 = 52 – x2

    Như vậy AC = 25−x2

    Áp dụng định lí Phytagoras cho tam giác ABD:

    AB2 + AD2 = BD2

    ⇒ AD2 = 62 – x2

    Như vậy AD = 36−x2

    b) Giải phương trình AB + AC + BC = 12

    ⇒ x + 5 + 25−x2 = 12

    ⇒ 25−x2 = 7 – x

    ⇒ 25 – x2 = (7 – x)2

    ⇒ 2x2 – 14x + 24 = 0

    ⇒ x = 4 hoặc x = 3

    Thay lần lượt các giá trị trên vào phương trình AB + AC + BC = 12 ta thấy x = 4 và  x = 3 đều thoả mãn. Vậy x = 4 hoặc x = 3 để chu vi tam giác ABC là 12.

    c) Ta có AD = 2AC

    ⇒ 36−x2 = 225−x2

    ⇒ 36 – x2 = 100 – 4x2

    ⇒ 3x2  –  64 = 0

    ⇒ x = 833 hoặc x = -833 mà x > 0 nên x = 833.

    Thay x = 833 vào phương trình AD = 2AC thấy thỏa mãn. Vậy x = 833.

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải SBT Toán 10 trang 19 Tập 2

    Giải SBT Toán 10 trang 20 Tập 2

    Giải SBT Toán 10 trang 21 Tập 2

    Giải SBT Toán 10 trang 22 Tập 2

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

    Bài tập cuối chương 6

    Bài 1: Dấu của tam thức bậc hai

    Bài 2: Giải bất phương trình bậc hai một ẩn

    Bài 3: Phương trình quy về phương trình bậc hai

    Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài tập cuối chương 7

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 759 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: