Giải SBT Toán 10 trang 20 Tập 2 Chân trời sáng tạo

Giải SBT Toán 10 trang 20 Tập 2 Chân trời sáng tạo

Câu 5 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1.

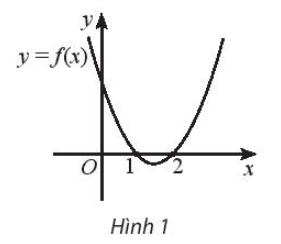
Tập nghiệm của bất phương trình $f\left(x\right)\ge 0$ là:

A. $\left(1;2\right)$;

B. $\left[1;2\right]$;

C. $\left(-\infty ;1\right)\cup \left(2;+\infty \right)$;

D. $\left(-\infty ;1\right]\cup \left[2;+\infty \right)$.

Lời giải:

Đáp án đúng là D

Tập nghiệm của bất phương trình $f\left(x\right)\ge 0$ là $\left(-\infty ;1\right]\cup \left[2;+\infty \right)$.

Câu 6 trang 20 SBT Toán 10 Tập 2: Bất phương trình nào có tập nghiệm là (2; 5)?

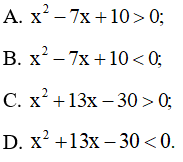
Lời giải:

Đáp án đúng là B

+) Tam thức bậc hai f ( x ) = x² – 7x +10 có ∆ = ( – 7)² – 4.1.10 = 9 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 2 và x₂ = 5, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < 2 hoặc x > 5.

f ( x ) < 0 với 2 < x < 5.

Do đó A sai, B đúng.

+) Tam thức bậc hai f ( x ) = $x^2+13x-30$ có ∆ = 13² – 4.1.(– 30) = 289 > 0 nên f(x) hai nghiệm phân biệt x₁ = 2 và x₂ = –15, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < –15 hoặc x > 2.

f ( x ) < 0 với –15 < x < 2.

Do đó C, D sai.

Vậy đáp án đúng là B.

Câu 7 trang 20 SBT Toán 10 Tập 2: Tập xác định của hàm số$y=\frac{1}{\sqrt{9x^2-3x-2}}+\sqrt{3-x}$ là:

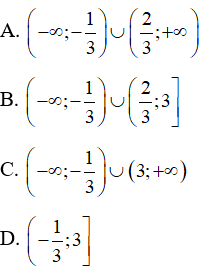
Lời giải:

Đáp án đúng là B

Hàm số trên xác định khi và chỉ khi 3 – x ≥ 0 và 9x² – 3x – 2 > 0

+) Ta có 3 – x ≥ 0 khi và chỉ khi x ≤ 3 (1)

+) Xét tam thức bậc hai f ( x ) = 9x² – 3x – 2 có ∆ = (– 3)² – 4.9.(– 2) = 81 > 0 nên f(x) có hai nghiệm phân biệt x₁ = $\frac{2}{3}$ và x₂ = $\frac{-1}{3}$, và a = 9 > 0 nên f ( x ) > 0 với $\left(-\infty ;\frac{-1}{3}\right)\cup \left(\frac{2}{3};+\infty \right)$ (2)

Từ (1) và (2) suy ra tập xác định của hàm số trên là $\left(-\infty ;-\frac{1}{3}\right)\cup \left(\frac{2}{3};3\right]$.

Vậy đáp án đúng là B.

Câu 8 trang 20 SBT Toán 10 Tập 2: Với giá trị nào của tham số m thì phương trình $\left(2m+6\right)x^2+4mx+3=0$có hai nghiệm phân biệt?

A. $m<-\frac{3}{2}$ hoặc m > 3;

B. $-\frac{3}{2}<m<3;$

C. m < - 3  hoặc $-3<m<-\frac{3}{2}$ hoặc m > 3;

D. $-3<m<-\frac{3}{2}$ hoặc m > 3.

Lời giải:

Đáp án đúng là A

+) 2m + 6 = 0 ⇔ m = –3, khi đó phương trình trở thành –12x + 3 = 0 ⇒ x = $\frac{1}{4}$. Suy ra phương trình chỉ có một nghiệm duy nhất. Do đó không thỏa mãn.

+) 2m + 6 ≠ 0 ⇔ m ≠ –3

Khi đó phương trình $\left(2m+6\right)x^2+4mx+3=0$có hai nghiệm phân biệt khi và chỉ khi

∆ = (4m)² – 4.3.(2m + 6) > 0 hay 2m² – 3m – 9 > 0

Tam thức bậc hai f ( x ) = 2m² – 3m – 9 có hai nghiệm phân biệt x₁ = 3 và x₂ = $\frac{-3}{2}$,

a = 2 > 0 nên f ( x ) > 0 với x < $\frac{-3}{2}$ hoặc x > 3 (2)

Từ điều kiện (1) và (2) suy ra m < - 3  hoặc $-3<m<-\frac{3}{2}$ hoặc m > 3.

Vậy đáp án đúng là C.

Câu 9 trang 20 SBT Toán 10 Tập 2: Giá trị nào là nghiệm của phương trình $\sqrt{x^2+x+11}=\sqrt{-2x^2-13x+16}?$

A. x = – 5

B. $x=\frac{1}{3}$

C. Cả hai câu A, B đều đúng;

D. Cả hai câu A, B đều sai.

Lời giải:

Đáp án đúng là C

Bình phương hai vế của phương trình đã cho, ta được:

x² + x + 11 = –2x² – 13x + 16

⇒ 3x² + 14x – 5 = 0

⇒ x = $\frac{1}{3}$ hoặc x = –5.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{1}{3}$ hoặc x = –5 đều thỏa mãn.

Vì vậy phương trình đã cho có hai nghiệm x = $\frac{1}{3}$ và x = –5

Vậy đáp án đúng là C.

Câu 10 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{2x^2-3x-1}=\sqrt{3x^2-2x-13}?$

A. Phương trình có hai nghiệm phân biệt cùng dấu;

B. Phương trình có hai nghiệm phân biệt trái dấu;

C. Phương trình có một nghiệm;

D. Phương trinh vô nghiệm.

Lời giải:

Đáp án đúng là B

Bình phương hai vế của phương trình đã cho, ta được:

2x² – 3x – 1 = 3x² – 2x – 13

⇒ x² + x – 12 = 0

⇒ x = 3 hoặc x = –4.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 3 hoặc x = –4 đều thỏa mãn.

Suy ra phương trình đã cho có hai nghiệm x = 3 và x = –4. Vậy hai nghiệm của phương trình đã cho là hai nghiệm phân biệt trái dấu.

Đáp án đúng là B.

Câu 11 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{5x^2+27x+36}=2x+5?$

A. Phương trình có một nghiệm;

B. Phương trình vô nghiệm;

C. Tổng các nghiệm của phương trình là -7;

D. Các nghiệm của phương trình đều không bé hơn $\frac{-5}{2}$.

Lời giải:

Đáp án đúng là A

Bình phương hai vế của phương trình đã cho, ta được:

5x² + 27x + 36 = 4x² + 20x + 25

⇒ x² + 7x + 11 = 0

⇒ x = $\frac{-7+\sqrt{5}}{2}$ hoặc x = $\frac{-7-\sqrt{5}}{2}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{-7+\sqrt{5}}{2}$ thỏa mãn.

Vì vậy đáp án A đúng.

Câu 12 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hai hàm số bậc hai f(x) = ax² + bx + c và g(x) = dx² + ex + h như Hình 2.

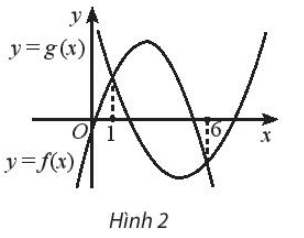
Khẳng định nào đúng với phương trình $\sqrt{{\text{ax}}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+h}?$

A. Phương trình có hai nghiệm phân biệt là x = 1 và x = 6,

B. Phương trình có 1 nghiệm là x = l;

C. Phương trình có 1 nghiệm là x = 6;

D. Phương trình vô nghiệm.

Lời giải:

Đáp án đúng là B

Xét phương trình $\sqrt{{\text{ax}}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+h}$

Bình phương hai vế ta được f ( x ) = g ( x )

Đồ thị hàm số f ( x ) và g ( x ) giao nhau tại hai điểm x = 1 và x = 6. Tuy nhiên tại

x = 6 thì g ( x ) < 0 và f ( x ) < 0 nên không thỏa mãn.

Vậy phương trình có 1 nghiệm là x = 1.

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 19 Tập 2

Giải SBT Toán 10 trang 21 Tập 2

Giải SBT Toán 10 trang 22 Tập 2

Giải SBT Toán 10 trang 23 Tập 2