Giải SBT Toán 10 trang 22 Tập 2 Chân trời sáng tạo
Với Giải SBT Toán 10 trang 22 Tập 2 trong Bài tập cuối chương 7 Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 22.
Giải SBT Toán 10 trang 22 Tập 2 Chân trời sáng tạo
Bài 4 trang 22 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
a)
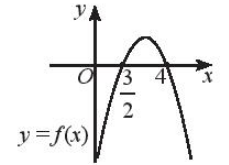
b)
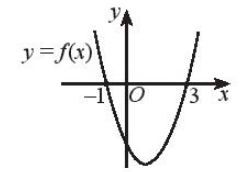
c)
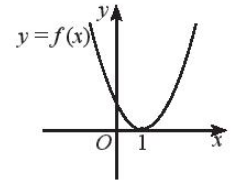
d)

e)
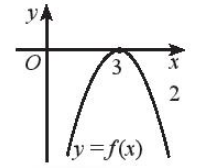
g)
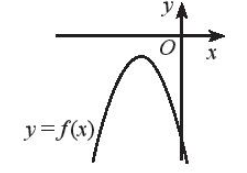
Lời giải:
a) Ta thấy đồ thị hàm số f ( x ) cắt trục hoành tại hai điểm x = và x = 4, khi ≤ x ≤ 4 thì đồ thị hàm số nằm trên trục hoành nên khi ≤ x ≤ 4.
Vậy f(x) ≥ 0 khi x ∈ .
b) khi đồ thị hàm số f ( x ) nằm trên trục hoành hay x < –1 hoặc x > 3.
Vậy f(x) > 0 khi (– ∞; – 1) ∪ (3; +∞).
c) Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại x = 1.
Với x ≠ 1 đồ thị hàm số nằm hoàn toàn phía trên trục hoành.
Do đó f(x) ≤ 0 khi x = 1.
Vậy f(x) ≤ 0 khi x = 1.
d) vô nghiệm vì ta thấy đồ thị hàm số f ( x ) hoàn toàn nằm trên trục hoành.
Vậy không tồn tại giá trị của x để f(x) < 0.
e) Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại x = 3.
Đồ thị nằm hoàn toàn phía dưới trục hoành với x ≠ 3.
Do đó khi x ≠ 3.
Vậy f(x) < 0 khi x ≠ 3.
g) Ta có thể thấy đồ thị hàm số f ( x ) hoàn toàn nằm dưới trục hoành nên với mọi x ∈ ℝ.
Vậy f(x) ≤ 0 với mọi x ∈ ℝ.
Bài 5 trang 22 SBT Toán 10 Tập 2: Giải các phương trình sau:
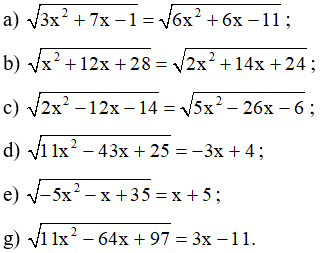
Lời giải:
a)
Bình phương hai vế của phương trình đã cho, ta được:
3x2 + 7x – 1 = 6x2 + 6x – 11
⇒ 3x2 – x – 10 = 0
⇒ x = hoặc x = 2.
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn. Vậy phương trình đã cho có nghiệm x = 2.
b)
Bình phương hai vế của phương trình đã cho, ta được:
x2 + 12x + 28 = 2x2 + 14x + 24
⇒ x2 + 2x – 4 = 0
⇒ x = –1 + hoặc x = –1 – .
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = –1 + thỏa mãn.
Vậy phương trình đã cho có nghiệm x = –1 + .
c)
Bình phương hai vế của phương trình đã cho, ta được:
2x2 – 12x – 14 = 5x2 – 26x – 6
⇒ 3x2 – 14x + 8 = 0
⇒ x = 4 hoặc x =
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 4 và x = đều không thỏa mãn. Vậy phương trình đã cho vô nghiệm.
d)
Bình phương hai vế của phương trình đã cho, ta được:
11x2 – 43x + 25 = 9x2 – 24x + 16
⇒ 2x2 – 19x + 9 = 0
⇒ x = 9 hoặc x =
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = thỏa mãn. Vậy phương trình đã cho có nghiệm x = .
e)
Bình phương hai vế của phương trình đã cho, ta được:
–5x2 – x + 35 = x2 + 10x + 25
⇒ 6x2 + 11x – 10 = 0
⇒ x = hoặc x =
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = hoặc x = đều thỏa mãn.
Vậy phương trình đã cho có nghiệm x = và x = .
g)
Bình phương hai vế của phương trình đã cho, ta được:
11x2 – 64x + 97 = 9x2 – 66x + 121
⇒ 2x2 + 2x – 24 = 0
⇒ x = 3 hoặc x = –4
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 3 và x = –4
đều không thỏa mãn.
Vậy phương trình đã cho vô nghiệm.
Bài 6 trang 22 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:
a)
b)
Lời giải:
a)
Hàm số trên xác định khi và chỉ khi –x2 + 6x – 2 ≥ 0
Tam thức bậc hai f ( x ) = –x2 + 6x – 2 có hai nghiệm phân biệt x1 = 3 + và
x2 = 3 – , a = –1 < 0 nên f ( x ) ≥ 0 khi 3 – ≤ x ≤ 3 +.
Vậy tập xác định của hàm số trên là D = .
b)
Hàm số trên xác định khi và chỉ khi x – 2 ≠ 0 và –x2 + 3x –2 ≥ 0.
+) Ta có x – 2 ≠ 0 khi và chỉ khi x ≠ 2 (1)
+)Tam thức bậc hai f ( x ) = –x2 + 3x –2 có hai nghiệm phân biệt x1 = 1 và x2 = 2,
a = –1 < 0 nên f ( x ) ≥ 0 khi 1 ≤ x ≤ 2 (2)
Từ (1) và (2) suy ra tập xác định của hàm số là .
Vậy tập xác định của hàm số là D = .
Bài 7 trang 22 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:
a) là một tam thức bậc hai âm với mọi ;
b) là một tam thức bậc hai có nghiệm;
c) Phương trình vô nghiệm,
d) Bất phương trình có tập nghiệm là .
Lời giải:
a) f ( x ) là một tam thức bậc hai âm với mọi x ∈ ℝ khi và chỉ khi a = m – 3 < 0 và
∆’ < 0.
+) Ta có: m – 3 < 0 khi và chỉ khi m < 3.
+) ∆’ = m2 + (m – 3).m = 2m2 – 3m < 0 khi và chỉ khi 0 < m <
Vậy để là một tam thức bậc hai âm với mọi x ∈ ℝ thì
0 < m < .
b) f ( x ) là một tam thức bậc hai có nghiệm khi và chỉ khi m – 2 ≠ 0 và ∆’ ≥ 0.
+) Ta có m – 2 ≠ 0 khi và chỉ khi m ≠ 2
+) Ta có ∆’ = (m + 3)2 – 5.(m – 3).(m – 2) = –4m2 + 31m – 21 ≥ 0 tức là
≤ m ≤ 7.
Vậy ≤ m < 2 và 2 < m ≤ 7 thì f(x) là một tam thức bậc hai có nghiệm.
c) Phương trình vô nghiệm khi và chỉ khi
∆ = ( 3m – 1 )2 – 16( m + 1 ) < 0 hay 9m2 – 22m – 15 < 0 tức là < m < 3.
Vậy < m < 3 thì phương trình đã cho vô nghiệm.
d) Xét tam thức bậc hai f(x) = 2x2 + 2.(m – 3)x + 3(m2 – 3) có a = 2 > 0 và ∆’ = ( m – 3 )2 – 6( m2 – 3 ) = m2 – 6m + 9 – 6m2 + 18 = – 5m2 – 6m + 27
Suy ra f(x) ≥ 0 với mọi x ∈ ℝ khi a = 2 > 0 và ∆’ = –5m2 – 6m + 27 ≤ 0 tức là m ≤ –3 hoặc m ≥ .
Vậy m ≤ –3 hoặc m ≥ .
Bài 8 trang 22 SBT Toán 10 Tập 2: Người ta thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao h0 (m) so với bề mặt của Mặt Trăng với vận tốc v0 (m/s) thì độ cao của bóng sau t giây được cho bởi hàm số với g = 1,625 m/s2 là gia tốc trọng trường của Mặt Trăng.
a) Biết độ cao ban đầu của quả bóng vào các thời điểm 8 giây và 12 giây lần lượt là 30 m và 5 m, hãy tìm vận tốc ném; độ cao ban đầu của quả bóng và viết công thức h(t).
b) Quả bóng đạt độ cao trên 29 m trong bao nhiêu giây?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Lời giải:
a) Ta có h ( t ) = –0,8125t2 + v0t + h0
Ta có h(8) = 30 và h(12) = 5
Do đó hay
Vậy h ( t ) = –0,8125t2 + 10t + 2.
b) Quả bóng đạt độ cao trên 29 m khi và chỉ khi –0,8125t2 + 10t + 2 > 29 hay
–0,8125t2 + 10t – 27 > 0
Xét tam thức bậc hai f(t) = –0,8125t2 + 10t – 27, có a = –0,8125 < 0 và ∆ = 102 – 4.(–0,8125).(– 27) = 12,25 > 0 suy ra f(t) có hai nghiệm phân biệt t1 = 8,31 và 4.
Do đó f(t) > 0 khi 4 < t < 8,31.
Vậy quả bóng ở độ cao trên 29m trong khoảng ít hơn 8,31 – 4 = 4,31 giây.
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải SBT Toán 10 trang 19 Tập 2
Giải SBT Toán 10 trang 20 Tập 2
Giải SBT Toán 10 trang 21 Tập 2
Giải SBT Toán 10 trang 23 Tập 2
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu
Bài 1: Dấu của tam thức bậc hai
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
