Câu hỏi:
09/10/2024 8,655
Cho 0° < α < 90°. Kết luận nào sau đây đúng
Cho 0° < α < 90°. Kết luận nào sau đây đúng
A. tan(α) > 0; cot(α) > 0;
A. tan(α) > 0; cot(α) > 0;
B. tan(α) < 0; cot(α) < 0;
B. tan(α) < 0; cot(α) < 0;
C. tan(α) > 0; cot(α) < 0;
C. tan(α) > 0; cot(α) < 0;
D. tan(α) < 0; cot(α) > 0.
D. tan(α) < 0; cot(α) > 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Phương pháp giải:
- Áp dụng tính chất của giá trị lượng giác đặc biệt,cách xác định góc phần tư trong lượng giác để làm
*Lời giải:
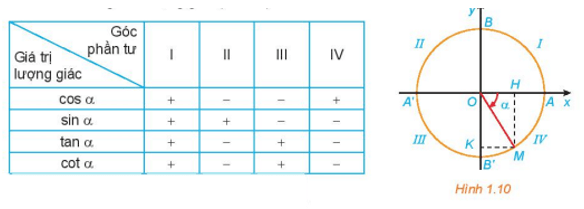
Vì 0° < α < 90° (Góc phần tư thứ 1) nên tan(α) > 0; cot(α) > 0.
*Các lý thuyết thêm cần nằm
Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn M trên đường tròn lượng giác.
Các Góc Phần Tư Trong Mặt Phẳng Tọa Độ
- Góc phần tư thứ nhất (Q1): Tọa độ x và y đều dương (x>0, y>0).
- Góc phần tư thứ hai (Q2): Tọa độ x âm và tọa độ y dương (x<0, y>0).
- Góc phần tư thứ ba (Q3): Tọa độ x và y đều âm (x<0, y<0).
- Góc phần tư thứ tư (Q4): Tọa độ x dương và tọa độ y âm (x>0, y<0).
Cách Xác Định Góc Phần Tư
-
Xác định tọa độ của điểm cần xét, được biểu diễn dưới dạng (x,y).
-
Kiểm tra dấu của tọa độ x và y để xác định góc phần tư:
- Nếu x>0 và y>0, điểm nằm ở góc phần tư thứ nhất (Q1).
- Nếu x<0 và y>0, điểm nằm ở góc phần tư thứ hai (Q2).
- Nếu x<0 và y<0, điểm nằm ở góc phần tư thứ ba (Q3).
- Nếu x>0 và y<0, điểm nằm ở góc phần tư thứ tư (Q4).
Bảng Tóm Tắt Các Góc Phần Tư
| Góc Phần Tư | Điều Kiện Tọa Độ | Ví Dụ Tọa Độ |
|---|---|---|
| Q1 | x>0,y>0 | (2, 3) |
| Q2 | x<0,y>0 | (-2, 3) |
| Q3 | x<0,y<0 | (-2, -3) |
| Q4 | x>0,y<0 | (2, -3) |
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Trắc nghiệm Giá trị lượng giác của một cung có đáp án – Toán lớp 10
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 5:
Kết quả rút gọn của biểu thức A=cos(−108∘).cot72∘tan(−162∘).sin108∘−tan18∘ là :
Kết quả rút gọn của biểu thức A=cos(−108∘).cot72∘tan(−162∘).sin108∘−tan18∘ là :
Câu 6:
Giá trị của biểu thức M=tan230∘+sin260∘−cos245∘cot2120∘+cos2150∘ bằng:
Giá trị của biểu thức M=tan230∘+sin260∘−cos245∘cot2120∘+cos2150∘ bằng:
Câu 13:
Biết tanα = 2, giá trị của biểu thức M=3sinα−2cosα5cosα+7sinα bằng:
Biết tanα = 2, giá trị của biểu thức M=3sinα−2cosα5cosα+7sinα bằng: