Toán lớp 5 trang 110 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Với giải bài tập Toán lớp 5 trang 110 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán lớp 5.
Giải Toán lớp 5 trang 110 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Video giải Toán lớp 5 trang 110 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Toán lớp 5 trang 110 Bài 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 5dm, chiều rộng 4dm và chiều cao 3dm.
Lời giải
Diện tích xung quanh của hình hộp chữ nhật là:
(5 + 4) × 2 × 3 = 54 (dm2)
Diện tích mặt đáy của hình hộp chữ nhật là:
5 × 4 = 20 (dm)
Diện tích toàn phần của hình hộp chữ nhật là:
54 + 20 + 20 = 94 (dm2)
Đáp số: 54dm2 và 94dm2
Toán lớp 5 trang 110 Bài 2: Một người thợ gò một cái thùng tôn không nắp dạng hình chữ nhật có chiều dài 6dm, chiều rộng 4 dm và chiều cao 9dm. Tính diện tích tôn dùng để làm thùng (không tính mép hàn).
Lời giải
Diện tích xung quanh của cái thùng là:
(6 + 4) × 2 × 9 = 180 (dm2)
Diện tích mặt đáy của cái thùng là:
6 × 4 = 24 (dm2)
Diện tích tôn để làm thùng là:
180 + 24 = 204 (dm2)
Đáp số: 204 dm2
Bài giảng Toán lớp 5 trang 110 Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Xem thêm lời giải bài tập Toán lớp 5 hay, chi tiết khác:
Toán lớp 5 trang 110 Luyện tập
Toán lớp 5 trang 111 Diện tích xung quanh và diện tích toàn phần của hình lập phương
Toán lớp 5 trang 112 Luyện tập
Toán lớp 5 trang 113, 114 Luyện tập chung
Toán lớp 5 trang 115 Thể tích của một hình
-------------------------------------------------------------------------------------
Bài tập Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Các dạng toán về Hình hộp chữ nhật lớp 5 và cách giải
Bài tập Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
---------------------------------------------------------------------
Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật lớp 5
1. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
a) Định nghĩa
- Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
- Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.
b) Quy tắc
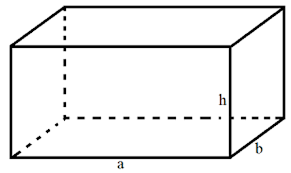
Giả sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là h.
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
Sxq = (a + b) × 2 × h
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Stp = Sxq + Sđáy × 2 = (a + b) x 2 x h + 2 x a x b
Lưu ý:
- Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với 2.
- Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.
2. Một số dạng bài tập
Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật
Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.
Bài giải
Chu vi đáy của hình hộp chữ nhật là:
(8 + 6) × 2 = 28 (cm)
Diện tích xung quanh của hình hộp chữ nhật đó là:
28 × 4 = 112 (cm2)
Diện tích một đáy là:
8 × 6 = 48 (cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
112 + 48 × 2 = 208(cm2)
Đáp số: Diện tích xung quanh: 112cm2
Diện tích toàn phần: 208cm2
Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật
Phương pháp:
*) Từ công thức Sxq = (a + b) x 2 x h:
- Tìm chiều cao theo công thức: h = Sxq : [(a + b) x 2] = Sxq: (a + b) : 2;
- Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = Sxq : h.
*) Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.
Ví dụ: Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.
Bài giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
14,5 × 2 = 29 (m)
Chiều cao của hình hộp chữ nhật đó là:
217,5 : 29 = 7,5 (m)
Đáp số: 7,5m
Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường …)
Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
Ví dụ: Một căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Người ta muốn quét vôi các bức tường xung quanh và trần của căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m2 (biết rằng chỉ quét vôi bên trong phòng)?
Bài giải
Đổi 48dm = 4,8m
Diện tích xung quanh của căn phòng đó là:
(6 + 4,8) × 2 × 4 = 86,4 (m2)
Diện tích trần của căn phòng đó là:
6 × 4,8 = 28,8 (m2)
Diện tích cần quét vôi là:
86,4 + 28,8 – 12 = 103,2 (m2)
Đáp số: 103,2m2
Xem thêm các chương trình khác:
