Toán lớp 5 trang 93, 94 Diện tích hình thang
Với giải bài tập Toán lớp 5 trang 93, 94 Diện tích hình thang chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán lớp 5.
Giải Toán lớp 5 trang 93, 94 Diện tích hình thang
Video giải Toán lớp 5 trang 93, 94 Diện tích hình thang
Toán lớp 5 trang 93 Bài 1: Tính diện tích hình thang biết:
a) Độ dài hai đáy lần lượt là 12cm và 8cm; chiều cao là 5cm.
b) Độ dài hai đáy lần lượt là 9,4m và 6,6m; chiều cao là 10,5m.
Lời giải
a) Diện tích hình thang là:
b) Diện tích hình thang là:
Toán lớp 5 trang 94 Bài 2: Tính diện tích mỗi hình thang sau:
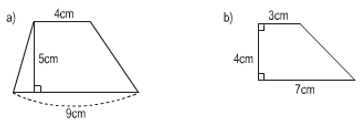
Lời giải
a) Diện tích hình thang là:
b, Diện tích hình thang là:
Toán lớp 5 trang 94 Bài 3: Một thửa ruộng hình thang có độ dài hai đáy lần lượt là 110m và 90,2m. Chiều cao bằng trung bình cộng của hai đáy . Tính diện tích của thửa ruông đó.
Lời giải
Chiều cao của thửa ruộng hình thang là:
(110 + 90,2) : 2 = 100,1 (m)
Diện tích thửa ruộng đó là:
Đáp số: 10020,01m2
Bài giảng Toán lớp 5 trang 93, 94 Diện tích hình thang
Xem thêm lời giải bài tập Toán lớp 5 hay, chi tiết khác:
Toán lớp 5 trang 95 Luyện tập chung
Toán lớp 5 trang 96, 97 Hình tròn. Đường tròn.
Toán lớp 5 trang 98 Chu vi hình tròn
------------------------------------------------------------------------
Bài tập Diện tích hình thang
Giải Vở bài tập Toán lớp 5 trang 5 Diện tích hình thang
Giải Sách bài tập Toán lớp 5 Hình thang. Diện tích hình thang
Các dạng toán về Hình thang lớp 5 và cách giải
Bài tập Hình thang. Diện tích hình thang
-------------------------------------------------------------------------
Lý thuyết Hình thang. Diện tích hình thang lớp 5
1. Hình thang
a) Định nghĩa
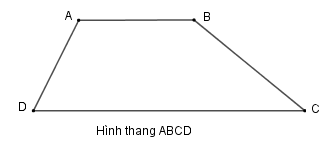
Hình thang ABCD có:
- Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.
- Hai cạnh đáy là hai cạnh đối diện song song.
Hình thang có một cặp cạnh đối diện song song.
Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.
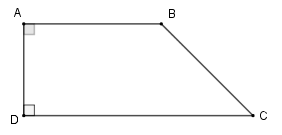
b) Đường cao của hình thang
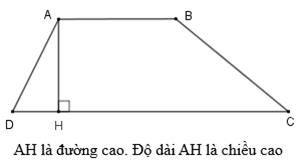
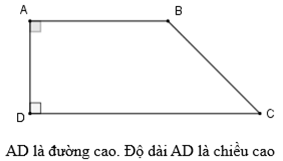
2. Diện tích hình thang
Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
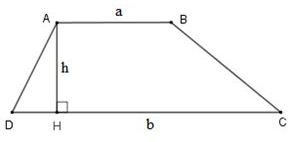
(S là diện tích; a, b là độ dài các cạnh đáy; h là chiều cao)
Ví dụ 1: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18cm và 14cm; chiều cao là 9cm.
Phương pháp giải: Độ dài hai đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.
Bài giải
Diện tích hình thang đó là:
Đáp số:
Ví dụ 2: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 4m và 25dm; chiều cao là 32dm.
Phương pháp giải: Độ dài hai đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đó, 4m = 40dm, sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.
Bài giải
Đổi: 4m = 40dm
Diện tích hình thang đó là:
Đáp số: 1040dm2
3. Một số dạng bài tập
Dạng 1: Tính diện tích hình thang khi biết độ dài hai đáy và chiều cao
Phương pháp:
Áp dụng công thức: hoặc
(S là diện tích, a, b là độ dài các cạnh đáy, h là chiều cao)
Dạng 2: Tính tổng độ dài hai đáy khi biết diện tích và chiều cao
Phương pháp: Từ công thức tính diện tích hoặc ta có công thức tính độ dài hai đáy như sau:
Lưu ý: Đề bài thường cho hiệu của hai đáy hoặc tỉ số giữa hai đáy và yêu cầu tìm độ dài của mỗi đáy. Học sinh cần nhớ hai dạng toán tổng – hiệu và tổng – tỉ.
Dạng 3: Tính chiều cao khi biết diện tích và độ dài hai đáy
Phương pháp: Từ công thức tính diện tích hoặc , ta có công thức tính chiều cao như sau hoặc .
Dạng 4: Toán có lời văn
Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.
Xem thêm các chương trình khác:
