50 bài tập Tìm hai số khi biết hiệu và tỉ của hai số đó lớp 4 và cách giải

Tìm hai số khi biết hiệu và tỉ của hai số đó lớp 4 và cách giải

I/ Lý thuyết

Để giải bài toán tìm hai số khi biết hiệu và tỉ số ta có thể làm như sau:

Bước 1: Vẽ sơ đồ biểu diễn hai số đó.

Bước 2: Tìm hiệu số phần bằng nhau.

Bước 3: Tìm số lớn hoặc số bé:

Số lớn = (Hiệu: hiệu số phần bằng nhau) × số phần của số lớn;

Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé.

Bước 4. Kết luận đáp số

(Học sinh có thể tiến hành thêm bước thử lại để kiểm chứng kết quả)

II/ Các dạng bài tập

II.1/ Dạng 1: Cho biết cả hiệu và tỉ số

1. Phương pháp giải

Bước 1: Vẽ sơ đồ biểu diễn hai số đó.

Bước 2: Tìm hiệu số phần bằng nhau.

Bước 3: Tìm số lớn hoặc số bé:

Số lớn = (Hiệu: hiệu số phần bằng nhau) × số phần của số lớn;

Số bé = (Hiệu : hiệu số phần bằng nhau) × số phần của số bé.

Bước 4. Kết luận đáp số

(Học sinh có thể tiến hành thêm bước thử lại để kiểm chứng kết quả)

2. Ví dụ minh họa

Ví dụ 1: Hiệu của hai số là 24. Tỉ số của hai số đó là $\frac{3}{5}$. Tìm hai số đó.

Lời giải:

Ta có sơ đồ:  

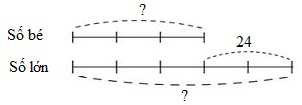
Theo sơ đồ, hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

Số bé là:

24 : 2 × 3 = 36

Số lớn là:

36 + 24 = 60

Đáp số: Số bé: 36; số lớn: 60                   

Ví dụ 2: Một hình chữ nhật có chiều dài hơn chiều rộng 12m. Tìm chiều dài, chiều rộng của hình đó, biết chiều dài bằng $\frac{7}{4}$ chiều rộng.

Lời giải:

Ta có sơ đồ:

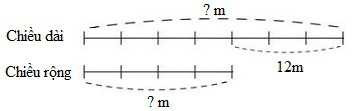
Theo sơ đồ, hiệu số phần bằng nhau là:

7 – 4 = 3 (phần)

Chiều dài hình chữ nhật là:

12 : 3 × 7 = 28 (m)

Chiều rộng hình chữ nhật là:

28 – 12 = 16 (m)

Đáp số: Chiều dài: 28m; Chiều rộng: 16m

II.2/ Dạng 2: Thiếu (ẩn) hiệu (Cho biết tỉ số, không cho biết hiệu)

1. Phương pháp giải

Tìm hiệu của hai số đưa về dạng tìm hai số khi biết hiệu và tỉ số cơ bản (dạng 1).

2. Ví dụ minh họa

Ví dụ 1: Hình chữ nhật có chiều dài bằng $\frac{3}{2}$ chiều rộng. Nếu tăng chiều rộng 20m thì hình chữ nhật trở thành hình vuông. Tính diện tích của hình chữ nhật?
Lời giải:

Nếu tăng chiều rộng 20m thì hình chữ nhật trở thành hình vuông nên chiều dài hơn chiều rộng 20m.

Hiệu số phần bằng nhau là:

3 – 2 = 1 (phần)

Chiều rộng của hình chữ nhật là:

20 : 1 × 2 = 40 (m)

Chiều dài của hình chữ nhật là:

40 + 20 = 60 (m)

Diện tích của hình chữ nhật là:

40 × 60 = 2400 (m²)

Đáp số: 2400 (m²).

Ví dụ 2: Năm nay tuổi mẹ gấp 4 lần tuổi con. Hai năm trước tuổi mẹ hơn tuổi con là 27 tuổi. Hỏi tuổi mẹ và tuổi con hiện nay?

Lời giải:

Hiệu số tuổi của hai mẹ con luôn không thay đổi nên mẹ nhiều hơn con 27 tuổi.

Hiệu số phần bằng nhau là:

4 – 1 = 3 (phần)

Tuổi con hiện nay là:

27 : 3 × 1 = 9 (tuổi)

Tuổi mẹ hiện nay là:

9 × 4 = 36 (tuổi)
Đáp số: Mẹ: 36 tuổi; con: 9 tuổi

Ví dụ 3: Một trại nuôi gà có số gà mái hơn số gà trống là 345 con. Sau khi mua thêm 25 con gà trống thì số gà trống bằng $\frac{3}{7}$ số gà mái. Hỏi đàn gà lúc đầu có bao nhiêu con? 

Lời giải:

Sau khi mua thêm 25 con gà trống thì gà mái nhiều hơn gà trống số con là:

345 – 25 = 320 (con)

Hiệu số phần bằng nhau là:

7 – 3 = 4 (phần)

Số gà trống ban đầu là:

320 : 4 × 3 – 25 = 215 (con)

Số gà mái ban đầu là:

215 + 345 = 560 (con)

Tổng số gà ban đầu là:

215 + 560 = 775 (con)

Đáp số: 775 (con)

II.3/ Dạng 3: Thiếu (ẩn) tỉ (Cho biết hiệu, không cho biết tỉ số)

1. Phương pháp giải

Tìm tỉ số của hai số đưa về dạng tìm hai số khi biết hiệu và tỉ số cơ bản (dạng 1).

2. Ví dụ minh họa

Ví dụ 1: Lớp 4A có 35 học sinh và lớp 4B có 33 học sinh cùng tham gia trồng cây. Lớp 4A trồng nhiều hơn lớp 4B 10 cây. Hỏi mỗi lớp trồng được bao nhiêu cây?

Lời giải:

Số cây lớp 4A trồng được bằng $\frac{35}{33}$ số cây lớp 4B trồng được.

Hiệu số phần bằng nhau:

35 – 33 = 2 (phần)

Lớp 4A trồng được số cây là:

10 : 2 × 35 = 175 (cây)

Lớp 4B trồng được số cây là:

175 – 10 = 165 (cây)

Đáp số: Lớp 4A: 175 (cây);

lớp 4B: 165 (cây).

Ví dụ 2: Có hai thùng dầu, thùng thứ nhất đựng ít thùng thứ hai 24 lít dầu. Biết 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?
Lời giải:

5 lần thùng thứ nhất bằng 3 lần thùng thứ hai nên số lít dầu ở thùng thứ nhất bằng $\frac{3}{5}$ số lít dầu ở thùng thứ hai.

Hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

Thùng thứ nhất đựng số lít dầu là:

24 : 2 × 3 = 36 (lít)

Thùng thứ hai đựng số lít dầu là:

36 + 24 = 60 (lít)

Đáp số: Thùng thứ nhất: 36 (lít);

thùng thứ hai: 60 (lít)
II.4/ Dạng 4: Ẩn cả hiệu và tỉ số

1. Phương pháp giải

Tìm hiệu và tỉ số của hai số đưa về dạng tìm hai số khi biết hiệu và tỉ số cơ bản (dạng 1).

2. Ví dụ minh họa

Ví dụ 1: Hiện nay An 8 tuổi và chị Mai 28 tuổi. Sau bao nhiêu năm nữa thì $\frac{1}{3}$ tuổi An bằng $\frac{1}{7}$ tuổi chị Mai.

Lời giải:

Khi $\frac{1}{3}$ tuổi An bằng $\frac{1}{7}$ tuổi chị Mai tức là khi tuổi An bằng $\frac{3}{7}$ tuổi chị Mai.

Hiệu số phần bằng nhau:

7 – 3 = 4 (phần)

Mai hơn em số tuổi là:

28 – 8 = 20 (tuổi)

Tuổi Mai khi thỏa mãn đề bài là:

20 : 4 × 7 = 35

Sau số năm để Mai 35 tuổi là:

35 – 28 = 7 (năm)

Đáp số: 7 (năm)

Ví dụ 2: Số thứ nhất hơn số thứ hai là 51. Nếu thêm 18 đơn vị vào số thứ nhất thì số thứ nhất gấp 4 lần thứ hai. Tìm hai số đó.
Lời giải:

Nếu thêm 18 đơn vị vào số thứ nhất thì số thứ nhất hơn số thứ hai số đơn vị là:    

51 + 18 = 69

Coi số thứ nhất là 4 phần số thứ hai là 1 phần.

Hiệu số phần bằng nhau là:

4 – 1 = 3 (phần)

Số thứ hai là:

69 : 3 × 1 = 23

Số thứ nhất là:

23 + 51 = 74
Đáp số: Số thứ nhất: 74;

số thứ hai: 23

III. Bài tập vận dụng

Bài 1: Hiệu của hai số là 85. Tỉ số của hai số đó là $\frac{3}{8}$. Tìm hai số đó?

Bài 2: Một lớp học có số học sinh nữ gấp đôi số học sinh nam. Nếu chuyển đi 3 học sinh nữ thì số học sinh nữ hơn số học sinh nam là 7 em. Lớp học đó có bao nhiêu học sinh?

Bài 3: Năm nay $\frac{1}{7}$ tuổi bố bằng $\frac{1}{2}$ tuổi con. Biết rằng bố hơn con 30 tuổi. Hỏi năm nay bố bao nhiêu tuổi?

Bài 4: Hiệu của hai số bằng số bé nhất có 3 chữ số. Tỉ số của hai số là $\frac{9}{5}$. Tìm hai số đó?

Bài 5: Tìm một số tự nhiên. Biết rằng khi viết thêm chữ số 0 vào bên phải số đó thì số đó tăng thêm 306 đơn vị.

Bài 6: Cha hơn con 36 tuổi. Tìm tuổi của mỗi người hiện nay. Biết 5 năm trước tuổi con bằng $\frac{1}{5}$ tuổi cha.

Bài 7: Tìm số có hai chữ số, biết rằng nếu ta viết thêm vào bên trái số đó chữ số 2 thì ta được số mới. Lấy số mới chia cho số cũ được thương là 9.

Bài 8: Tìm 2 số, biết rằng nếu ta viết thêm vào bên trái số đó chữ số 1 thì ta được số mới gấp 5 lần số cũ.

Bài 9: Tìm hai số biết tỉ số của chúng bằng $\frac{4}{7}$ và nếu lấy số lớn trừ đi số bé thì được kết quả bằng 360.

Bài 10: Tìm hai số có hiệu bằng 333, biết rằng nếu viết thêm một chữ số 0 vào bên phải số bé thì được số lớn.

Bài 11: Tìm hai số có tỉ số là $\frac{1}{9}$, biết rằng số lớn là số có ba chữ số và nếu xóa chữ số 4 ở hàng trăm của số lớn thì được số bé.

Bài 12: Tìm hai số có hiệu bằng 165, biết rằng nếu lấy số lớn chia cho số bé thì được thương là 7 và có số dư là 3.

Bài 13: Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 22m. Tính diện tích của mảnh vườn đó, biết rằng chiều rộng bằng  chiều dài.

Bài 14: Bố cao hơn con 70cm. Tỉ số giữa chiều cao của bố và chiều cao của con là 5 : 3. Tính chiều cao của bố và con.

Bài 15: Hình chữ nhật có chiều dài hơn chiều rộng 58m và chiều dài gấp 3 lần chiều rộng. Tính diện tích hình chữ nhật.

Bài 16: Tìm hai số biết tỉ số giữa chúng bằng  và nếu lấy số lớn trừ đi số bé thì được kết quả bằng 120.

Bài 17: Hiện nay bố 32 tuổi và An 8 tuổi. Hỏi bao nhiêu năm nữa tuổi của bố gấp 5 lần tuổi của An?

Bài 18: Tìm hai số có hiệu bằng 216, biết rằng nếu thêm một chữ số 0 vào bên phải số bé thì được số lớn. (Gợi ý: thêm 1 chữ số 0 vào bên phải số bé thì được số lớn → số lớn gấp số bé 10 lần)

Bài 19: Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 15m. Tính diện tích mảnh vườn đó, biết rằng chiều rộng bằng 3/4 chiều dài.

Bài 20: Một trường tiểu học có số học sinh nữ ít hơn số học sinh nam là 120 học sinh. Hỏi trường đó có bao nhiêu học sinh nam, bao nhiêu học sinh nữ, biết rằng số học sinh nữ bằng 5/7 số học sinh nam?

Bài 21: Hình chữ nhật có chiều dài bằng 3/2 chiều rộng. Nếu tăng chiều rộng 20 m thì hình chữ nhật trở thành hình vuông. Tính diện tích của hình chữ nhật.

Bài 22: Một lớp học có số học sinh nữ gấp đôi số học sinh nam. Nếu chuyển đi 3 học sinh nữ thì số học sinh nữ hơn số học sinh nam là 7 em. Hỏi lớp học đó có bao nhiêu học sinh?

Bài 23: Hiệu của hai số là 85. Tỉ số của hai số đó là 3/8. Tìm hai số đó.

Bài 24: Hiệu của hai số là 34. Tỉ số của hai số đó là 5/3. Tìm hai số đó?

Bài 25: Hiệu của hai số bằng 30. Số thứ nhất gấp 3 lần số thứ hai. Tìm hai số đó.

Xem thêm các dạng Toán lớp 4 hay, chọn lọc khác:

Tìm hai số khi biết tổng và hiệu của hai số đó lớp 4 và cách giải

Tìm hai số khi biết tổng và tỉ số của hai số đó lớp 4 và cách giải

Tính giá trị của biểu thức lớp 4 và cách giải

Toán quy luật lớp 4 và cách giải

Toán trung bình cộng lớp 4 và cách giải