Nội dung bài viết

    Xem thêm

    Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông

    Lời giải Bài 1.14 trang 19 Toán 12 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 1,965 08/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Kết nối tri thức Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

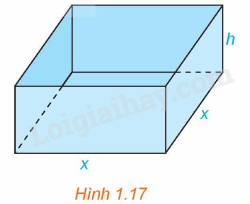
    Bài 1.14 trang 19 Toán 12 Tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108cm2 như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

    Tài liệu VietJack

    Lời giải:

    Hình hộp trên có độ dài cạnh đáy là x (cm, x>0) và chiều cao là h (cm, h>0)

    Diện tích bề mặt của hình hộp là 108cm2 nên x2+4xh=108⇒h=108−x24x(cm)

    Thể tích của hình hộp là: V=x2.h=x2.108−x24x=108x−x34(cm3)

    Ta có: V′=−3x2+1084,V′=0⇔x=6 (do x>0)

    Bảng biến thiên:

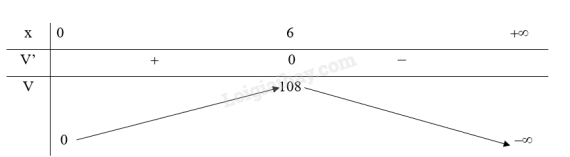
    Tài liệu VietJack

    Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy x=6cm

    Khi đó, chiều cao của hình hộp là: 108−624.6=3(cm).

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    HĐ1 trang 15 Toán 12 Tập 1: Cho hàm số y=f(x)=x2−2x với x∈[0;3], có đồ thị như Hình 1.15...

    Luyện tập 1 trang 17 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) y=2x−x2; b) y=−x+1x−1 trên khoảng (1;+∞)...

    HĐ2 trang 17 Toán 12 Tập 1: Xét hàm số y=f(x)=x3−2x2+1 trên đoạn [−1;2], với đồ thị như Hình 1.16...

    Luyện tập 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: a) y=2x3−3x2+5x+2 trên đoạn [0;2]; b) y=(x+1)e−x trên đoạn [−1;1]...

    Vận dụng trang 18 Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N(t)=−t3+12t2,0≤t≤12,...

    Bài 1.10 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) y=−x2+4x+3; b) y=x3−2x2+1 trên [0;+∞);...

    Bài 1.11 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) y=x4−2x2+3; b) y=x.e−x; c) y=xln⁡x;...

    Bài 1.12 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) y=2x3−6x+3 trên đoạn [−1;2];...

    Bài 1.13 trang 19 Toán 12 Tập 1: Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất...

    Bài 1.14 trang 19 Toán 12 Tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108cm2...

    Bài 1.15 trang 19 Toán 12 Tập 1: Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000cm3...

     

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 1: Tính đơn điệu và cực trị của hàm số

    Bài 3: Đường tiệm cận của đồ thị hàm số

    Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

    Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

    Bài tập cuối chương 1 trang 42

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,965 08/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: