Lý thuyết Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (mới 2024 + Bài Tập) - Vật lí 12

Tóm tắt lý thuyết Vật lí 12 Bài 5:Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen ngắn gọn, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Vật lí 12 Bài 2.

1 4,272 20/12/2023

Tải về

Trang trước

Trang sau

Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen

I. Vectơ quay

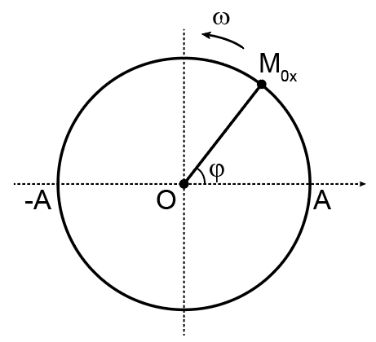
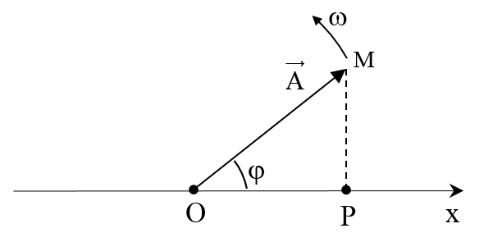
Mỗi dao động điều hòa được biểu diễn bằng một vectơ quay có đặc điểm:

+ Độ dài vectơ bằng biên độ A của dao động.

+ Tốc độ góc quay của vectơ đúng bằng tần số góc $ω$ của dao động.

+ Góc ban đầu chính là pha ban đầu φ của dao động.

Về bản chất, biểu diễn vectơ quay không khác gì so với biểu diễn chuyển động tròn đều.

$x = A \cos (ω t + φ)$

Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (ảnh 1)

II. Phương pháp giản đồ Fre – nen

- Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cũng phương, cùng tần số với hai dao động đó.

- Tổng hợp hai dao động điều hòa cùng phương, cùng tần số:

$x_{1} = A_{1} \cos (ω t + φ_{1})$

$x_{2} = A_{2} \cos (ω t + φ_{2}),$

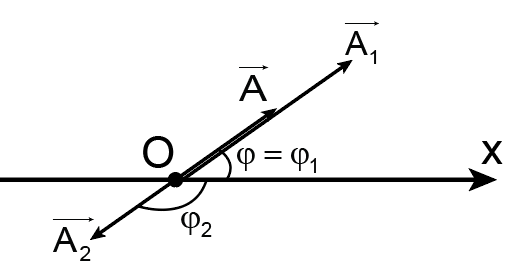
Ta sử dụng phương pháp giản đồ Fre – nen: Lần lượt vẽ hai vectơ quay biểu diễn hai phương trình dao động thành phần. Sau đó, vẽ vectơ tổng hợp của hai vectơ trên. Vectơ tổng là vectơ quay biểu diễn phương trình của dao động tổng hợp $x = A \cos (ω t + φ)$ .

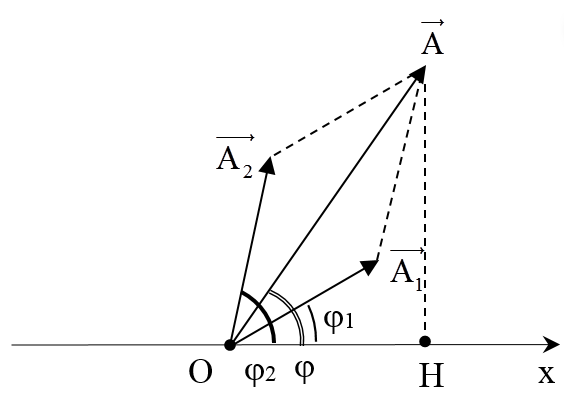
Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (ảnh 1)

Biên độ và pha ban đầu của dao động tổng hợp

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s (φ_{2} - φ_{1})}$

$\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c os φ_{1} + A_{2} c os φ_{2}}$

- Một số trường hợp đặc biệt cần lưu ý:

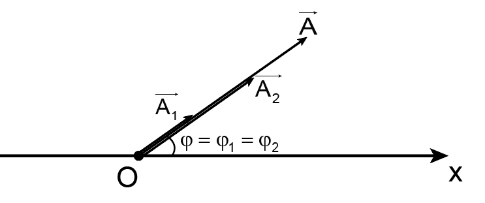
+ Hai dao động thành phần cùng pha: $Δ φ = φ_{2} - φ_{1} = 2 k π$ với $k = 0; \pm 1; \pm 2; ...$

Biên độ dao động tổng hợp: $A = A_{1} + A_{2}$

Ví dụ:

Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (ảnh 1)

+ Hai dao động thành phần ngược pha: $Δ φ = φ_{2} - φ_{1} = (2 k + 1) π$ với $k = 0; \pm 1; \pm 2; ...$

Biên độ dao động tổng hợp: $A = |A_{1} - A_{2}|$

Ví dụ:

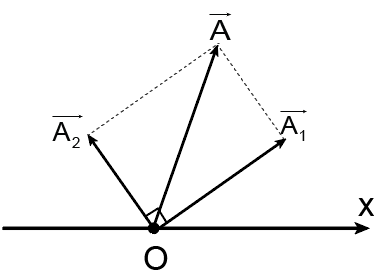
Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (ảnh 1)

+ Hai dao động thành phần vuông pha: $Δ φ = φ_{2} - φ_{1} = (2 k + 1) \frac{π}{2}$ với $k = 0; \pm 1; \pm 2; ...$

Biên độ dao động tổng hợp: $A = \sqrt{A_{1}^{2} + A_{2}^{2}}$

Ví dụ:

Lý thuyết Vật lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre – nen (ảnh 1)

- Trong mọi trường hợp, ta luôn có bất đẳng thức: $|A_{1} - A_{2}| \leq A \leq |A_{1} + A_{2}|$

Chú ý: Có thể sử dụng phép cộng lượng giác: $x = x_{1} + x_{2}$ khi tổng hợp hai dao động cùng biên độ.

Trắc nghiệm Vật Lí 11 Bài 5: Tổng hợp hai dao động điều hoà cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen

Câu 1. Một chất điểm thực hiện đồng thời hai dao động có phương trình li độ lần lượt là $x_{1} = A_{1} c o s(ω t + φ_{1})$ và $x_{2} = A_{2} c o s(ω t + φ_{2})$ . Biên độ dao động tổng hợp A được tính bằng biểu thức

A. $A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} . c o s (φ_{2} - φ_{1})}$

B. $A = \sqrt{A_{1}^{2} + A_{2}^{2} + A_{1} A_{2} . c o s (φ_{2} - φ_{1})}$

C. $A = \sqrt{A_{1}^{2} + A_{2}^{2} - A_{1} A_{2} . c o s (φ_{2} - φ_{1})}$

D. $A = \sqrt{A_{1}^{2} + A_{2}^{2} - 2 A_{1} A_{2} . c o s (φ_{2} - φ_{1})}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Biên độ dao động tổng hợp A được tính bằng biểu thức:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} . c o s (φ_{2} - φ_{1})}$

Câu 2. Một chất điểm thực hiện đồng thời hai dao động có phương trình li độ lần lượt là $x_{1} = A_{1} c o s(ω t + φ_{1})$ và $x_{2} = A_{2} c o s(ω t + φ_{2})$ . Pha ban đầu của dao động tổng hợp được tính bằng biểu thức

A. $\tan φ = \frac{A_{1} c o s φ_{1} + A_{2} s i n φ_{2}}{A_{2} c o s φ_{2} + A_{1} \sin φ_{1}}$

B. $\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}$

C. $\tan φ = \frac{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}$

D. $\tan φ = \frac{A_{1} c o s φ_{1} + A_{1} s i n φ_{1}}{A_{2} c o s φ_{2} + A_{2} \sin φ_{2}}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Pha ban đầu của dao động tổng hợp $\tan φ$ được tính bằng biểu thức:

$\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}$

Câu 3. Một vật thực hiện đồng thời hai dao động điều hòa

$\{\begin{cases} x_{1} = 6 c o s4 π t (cm) \\ x_{2} = 6 c o s (4 π t + \frac{π}{3}) (c m) \end{cases}$ .

Dao động tổng hợp của hai dao động trên có phương trình là

A. $x = 6 \sqrt{3} \cos (4 π t + \frac{π}{6}) (c m)$ .

B. $x = 6 \cos (4 π t + \frac{π}{3}) (c m)$ .

C. $x = 6 \cos (4 π t + \frac{π}{6}) (c m)$ .

D. $x = 6 \cos (4 π t) (c m)$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Dao động tổng hợp có dạng: $x = A c o s(ω t + φ) (cm)$

Ta có:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})}$

$= \sqrt{6^{2} + 6^{2} + 2.6.6. c o s (\frac{π}{3} - 0)} = 6 \sqrt{3} (c m)$

$\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}$

$= \frac{6. \sin 0 + 6. \sin \frac{π}{3}}{6. c o s 0 + 6. c o s \frac{π}{3}} = \frac{\sqrt{3}}{3}$

$\Rightarrow φ = \frac{π}{6}$

Vậy dao động tổng hợp của hai dao động trên là:

$x = 6 \sqrt{3} \cos (4 π t + \frac{π}{6}) (c m)$

Câu 4. Biên độ dao động tổng hợp của hai dao động cùng phương, cùng tần số phụ thuộc vào

A. biên độ dao động thứ nhất.

B. biên độ dao động thứ hai.

C. độ lệch pha của hai dao động thành phần.

D. Cả A, B và C đều đúng.

Hiển thị đáp án

Đáp án: D

Giải thích:

Công thức tính biên độ tổng hợp của hai dao động cùng phương, cùng tần số là

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})}$

Nhìn vào công thức ta thấy được, biên độ dao động tổng hợp phụ thuộc vào cả biên độ dao động thứ nhất, biên độ dao động thứ hai và độ lệch pha của hai dao động thành phần.

Câu 5. Hai dao động là cùng pha khi

A. $φ_{2} - φ_{1} = n π$ .

B. $φ_{2} - φ_{1} = 2 n π$ .

C. $φ_{2} - φ_{1} = (n - 1) π$ .

D. $φ_{2} - φ_{1} = (2 n - 1) π$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Hai dao động cùng pha khi độ lệch pha của chúng bằng số chẵn của π.

A – Sai, vì n có thể chẵn hoặc lẻ => Hai dao động có thể cùng pha hoặc ngược pha.

B – Đúng

C – Sai, vì (n – 1) có thể chẵn hoặc lẻ => Hai dao động có thể cùng pha hoặc ngược pha.

D – Sai, vì (2n – 1) là một số lẻ => hai dao động ngược pha.

Câu 6. Cho hai dao động điều hòa cùng phương, cùng tần số góc $ω = 5 π rad/s$ , với các biên độ $A_{1} = \frac{\sqrt{3}}{2} c m, A_{2} = \sqrt{3} c m$ và các pha ban đầu tương ứng $φ_{1} = \frac{π}{2}$ và $φ_{2} = \frac{5 π}{6}$ . Phương trình dao động tổng hợp của hai dao động trên là

A. x = $2, 3 c o s(5 π t + π) (c m)$ .

B. x = $2, 3 c o s(5 π t - π) (c m)$ .

C. x = $2, 3 c o s(5 π t + 0,73 π) (c m)$ .

D. x = $2, 3 c o s(5 π t - 0,73 π) (c m)$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Biên độ của dao động tổng hợp là:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})}$

$\Rightarrow A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})$

$= {(\frac{\sqrt{3}}{2})}^{2} + {(\sqrt{3})}^{2} + 2. \frac{\sqrt{3}}{2} . \sqrt{3} c o s (\frac{5 π}{6} - \frac{π}{2}) = \frac{21}{4}$

$\Rightarrow A = 2, 3 (c m)$

Pha ban đầu của dao động tổng hợp:

$\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}$

$= \frac{\frac{\sqrt{3}}{2} . \sin (\frac{π}{2}) + \sqrt{3} . \sin (\frac{5 π}{6})}{\frac{\sqrt{3}}{2} . c o s (\frac{π}{2}) + \sqrt{3} . c o s (\frac{5 π}{6})}$

$\Rightarrow φ = 0, 73 π (r a d)$

Vậy phương trình dao động tổng hợp là:

x = $2, 3 c o s(5 π t + 0,73 π) (c m)$

Câu 7. Dùng phương pháp giản đồ Fre – nen, có thể biểu diễn được dao động tổng hợp của hai dao động điều hòa

A. cùng phương, cùng biên độ.

B. cùng phương, cùng tần số.

C. khác phương, cùng tần số.

D. khác phương, khác tần số.

Hiển thị đáp án

Đáp án: B

Giải thích:

Dùng phương pháp giản đồ Fre – nen, có thể biểu diễn được dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số.

Câu 8. Cho hai dao động điều hòa cùng phương, có phương trình lần lượt là $x_{1} = A_{1} c o s ω t$ và $x_{2} = A_{2} c o s (ω t + \frac{π}{2})$ . Biên độ dao động tổng hợp của hai dao động này là

A. $A_{1}$ .

B. $A_{2}$ .

C. $A_{1} + A_{2}$ .

D. $\sqrt{A_{1}^{2} + A_{2}^{2}}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Độ lệch pha của hai dao động thành phần: $Δ φ = \frac{π}{2}$

Biên độ dao động tổng hợp:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})}$

$\Rightarrow A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})$

$= A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s \frac{π}{2}$

$\Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2}}$

Câu 9. Cho hai dao động điều hòa cùng phương, có phương trình lần lượt là $x_{1} = 4 c o s (π t - \frac{π}{6}) (c m)$ và $x_{2} = 4 c o s (π t - \frac{π}{2}) (c m)$ . Biên độ dao động tổng hợp của hai dao động này là

A. 4 cm.

B. $4 \sqrt{3} cm$ .

C. 12 cm.

D. $12 \sqrt{3} cm$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Biên độ dao động tổng hợp:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})}$

$\Rightarrow A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s(φ_{2} - φ_{1})$

${= 4}^{2} + 4^{2} + 2.4.4 c o s (- \frac{π}{2} + \frac{π}{6}) = 48$

$\Rightarrow A = 4 \sqrt{3} c m$

Câu 10. Cho hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ và có các pha ban đầu là $\frac{π}{3}$ và $\frac{π}{6}$ (phương trình dạng cos). Pha ban đầu của dao động tổng hợp hai dao động trên bằng

A. $\frac{π}{4}$ .

B. $\frac{π}{8}$ .

C. $\frac{2 π}{5}$ .

D. $\frac{3 π}{7}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} \cos φ_{1} + A_{2} \cos φ_{2}} = \frac{a \sin \frac{π}{3} + a \sin \frac{π}{6}}{a \cos \frac{π}{3} + a \cos \frac{π}{6}} \Rightarrow φ = \frac{π}{4}$

Xem thêm các bài tổng hợp lý thuyết Vật lí lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Bài 7: Sóng cơ và sự truyền sóng cơ

Lý thuyết Bài 8: Giao thoa sóng

Lý thuyết Bài 9: Sóng dừng

Lý thuyết Bài 10: Đặc trưng vật lí của âm

Lý thuyết Bài 11: Đặc trưng sinh lí của âm

1 4,272 20/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3