Trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Phần 2) có đáp án (Thông hiểu)
-
843 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Vị trí tương đối của hai đường thẳng \({d_1}:\frac{x}{2} - \frac{y}{3} = 1\) và d2: 6x – 4y – 8 = 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có \({d_1}:\frac{x}{2} - \frac{y}{3} = 1 \Leftrightarrow 3x - 2y - 6 = 0\).
Ta có:
⦁ Đường thẳng d1 có vectơ pháp tuyến \({\vec n_1} = \left( {3; - 2} \right)\).
⦁ Đường thẳng d2 có vectơ pháp tuyến \({\vec n_2} = \left( {6; - 4} \right)\).
Vì \(\frac{3}{6} = \frac{{ - 2}}{{ - 4}}\) nên \({\vec n_1}\) cùng phương với \({\vec n_2}\) (1)
Chọn A(2; 0) ∈ d1.
Thế tọa độ A(2; 0) vào phương trình d2, ta được: 6.2 – 4.0 – 8 = 4 ≠ 0.
Suy ra A(2; 0) ∉ d2 (2)
Từ (1), (2), ta suy ra d1 // d2.
Vậy ta chọn phương án A.
Câu 2:
06/11/2024 Xem đáp án
Đáp án đúng là: C
Lời giải:
⦁ d1 và d2 có vectơ chỉ phương lần lượt là \({\vec u_1} = \left( {1;2} \right),\,\,{\vec u_2} = \left( {1; - 4} \right)\).
Vì \(\frac{1}{1} \ne \frac{2}{{ - 4}}\) nên \({\vec u_1}\) không cùng phương với \({\vec u_2}\).
Do đó d1 cắt d2.
Vì vậy phương án A sai.
⦁ d3 và d4 có vectơ chỉ phương lần lượt là \({\vec u_3} = \left( { - 1;2} \right),\,\,{\vec u_4} = \left( { - 1;1} \right)\).
Vì \(\frac{{ - 1}}{{ - 1}} \ne \frac{2}{1}\) nên \({\vec u_3}\) không cùng phương với \({\vec u_4}\).
Do đó d3 cắt d4.
Vì vậy phương án B sai.
⦁ d5 và d6 có vectơ pháp tuyến lần lượt là \({\vec n_5} = \left( {1; - 1} \right),\,\,{\vec n_6} = \left( {1; - 1} \right)\).
Vì \(\frac{1}{1} = \frac{{ - 1}}{{ - 1}}\) nên \({\vec n_5}\) cùng phương với \({\vec n_6}\) (1)
Chọn M(0; 1) ∈ d5.
Thế tọa độ M(0; 1) vào phương trình d6, ta được: 0 – 1 + 10 = 9 ≠ 0.
Suy ra M(0; 1) ∉ d6 (2)
Từ (1), (2), ta suy ra d5 // d6.
Vì vậy phương án C đúng.
⦁ Tọa độ giao điểm của đường thẳng d7 và d8 thỏa hệ phương trình: \(\left\{ \begin{array}{l}2x - 5y - 7 = 0\\x - y - 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\)
Suy ra hệ phương trình đã cho có nghiệm duy nhất.
Khi đó d7 cắt d8.
Vì vậy phương án D sai.
Vậy ta chọn phương án C.
*Phương pháp giải
Dạng 1: Chứng minh hai đường thẳng song song
Phương pháp giải: Sử dụng một trong các cách sau
- Chứng minh hai đường thẳng đó đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng.
- Chứng minh hai đường thẳng đó cùng song song với một đường thẳng thứ ba.
- Áp dụng định lí về giao tuyến song song.
- Áp dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Dạng 2: Chứng minh bốn điểm đồng phẳng, ba đường thẳng đồng quy trong không gian
a. Chứng minh bốn điểm đồng phẳng
Phương pháp giải:
Chứng minh bốn điểm A, B, C, D đồng phẳng ta tìm hai đường thẳng a, b lần lượt đi qua hai trong bốn điểm trên và chứng minh a, b song song hoặc cắt nhau. Khi đó A, B, C, D thuộc mặt phẳng (a, b).
b. Chứng minh ba đường thẳng đồng quy
Phương pháp giải:
- Cách 1: Chứng minh đường thẳng thứ nhất đi qua giao điểm của hai đường thẳng còn lại.
- Cách 2: Chứng minh ba đường thẳng đôi một cắt nhau và chúng đôi một nằm trong ba mặt phẳng phân biệt
Bước 1: Xác định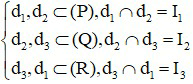 
với (P), (Q), (R) phân biệt
Bước 2: Kết luận d1,d2,d3 đồng quy tại I ≡ I1 ≡ I2 ≡ I3
*Lý thuyết:
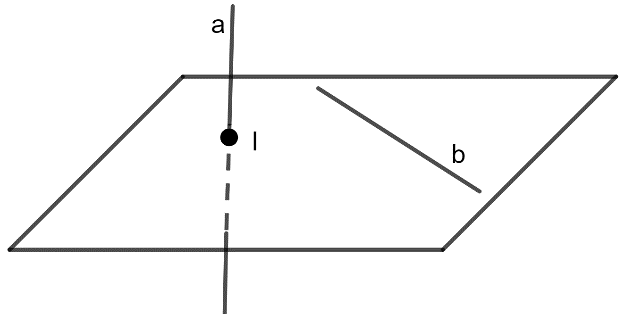
1. Vị trí tương đối giữa hai đường thẳng trong không gian
- Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng
- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng. Hai đường thẳng chéo nhau thì không có điểm chung.
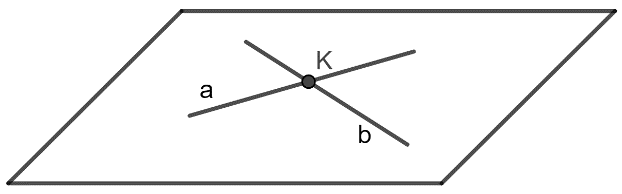
- Hai đường thẳng gọi là cắt nhau nếu chúng đồng phẳng và có một điểm chung
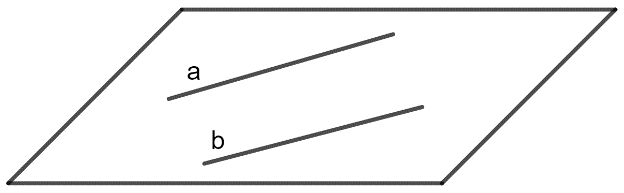
- Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung
- Như vậy, trong không gian, có 4 vị trí tương đối của hai đường thẳng, đó là: song song, trùng nhau, cắt nhau và chéo nhau.
- Khi nhắc đến hai đường thẳng phân biệt, thì ta hiểu là có 3 vị trí tương đối của hai đường thẳng đó (bỏ đi trường hợp trùng nhau).
Xem thêm
Điều kiện để đường thẳng song song với mặt phẳng và cách giải dạng các bài tập (2024)
Câu 3:
21/07/2024Góc giữa hai đường thẳng \({\Delta _1}:2x + 2\sqrt 3 y + \sqrt 5 = 0\) và \({\Delta _2}:y - \sqrt 6 = 0\) là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
∆1 và ∆2 có vectơ pháp tuyến lần lượt là \({\vec n_1} = \left( {2;2\sqrt 3 } \right),\,\,{\vec n_2} = \left( {0;1} \right)\).
Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {2.0 + 2\sqrt 3 .1} \right|}}{{\sqrt {{2^2} + {{\left( {2\sqrt 3 } \right)}^2}} .\sqrt {{0^2} + {1^2}} }} = \frac{{\sqrt 3 }}{2}\).
Suy ra (∆1, ∆2) = 30°.
Vậy ta chọn phương án D.
Câu 4:
19/07/2024Cho đường thẳng d: x – 2y + 1 = 0. Nếu đường thẳng ∆ đi qua điểm M(1; –1) và ∆ song song với d thì ∆ có phương trình:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 2} \right)\).
Vì ∆ // d nên ∆ nhận \({\vec n_d} = \left( {1; - 2} \right)\) làm vectơ pháp tuyến.
Đường thẳng ∆ đi qua M(1; –1) và có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 2} \right)\).
Suy ra phương trình tổng quát của ∆: 1(x – 1) – 2(y + 1) = 0.
⇔ x – 2y – 3 = 0.
Vậy ta chọn phương án A.
Câu 5:
22/07/2024Phương trình đường thẳng ∆ đi qua A(–3; 4) và vuông góc với đường thẳng d: 3x + 4y – 12 = 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {3;4} \right)\).
Vì ∆ ⊥ d nên ∆ nhận \({\vec n_d} = \left( {3;4} \right)\) làm vectơ chỉ phương.
Suy ra ∆ có vectơ pháp tuyến là \({\vec n_\Delta } = \left( {4; - 3} \right)\).
∆ đi qua điểm A(–3; 4) và có vectơ pháp tuyến \({\vec n_\Delta } = \left( {4; - 3} \right)\).
Suy ra phương trình tổng quát của ∆: 4(x + 3) – 3(y – 4) = 0.
⇔ 4x – 3y + 24 = 0.
Vậy ta chọn phương án A.
Câu 6:
22/07/2024Khoảng cách giữa hai đường thẳng song song 7x + y – 3 = 0 và 7x + y + 12 = 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta gọi d: 7x + y – 3 = 0 và ∆: 7x + y + 12 = 0.
Chọn M(0; 3) ∈ d.
Ta có \(d\left( {d,\Delta } \right) = d\left( {M,\Delta } \right) = \frac{{\left| {7.0 + 3 + 12} \right|}}{{\sqrt {{7^2} + {1^2}} }} = \frac{{3\sqrt 2 }}{2}\).
Vậy ta chọn phương án B.
Câu 7:
19/07/2024Khoảng cách từ điểm M(1; –1) đến đường thẳng ∆: \(\left\{ \begin{array}{l}x = 3 + 4t\\y = - 2 + 3t\end{array} \right.\) là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Đường thẳng ∆ có vectơ chỉ phương \(\vec u = \left( {4;3} \right)\).
Suy ra đường thẳng ∆ có vectơ pháp tuyến \(\vec n = \left( {3; - 4} \right)\).
Đường thẳng ∆ đi qua điểm A(3; –2) và có vectơ pháp tuyến \(\vec n = \left( {3; - 4} \right)\).
Suy ra phương trình tổng quát của ∆: 3(x – 3) – 4(y + 2) = 0.
⇔ 3x – 4y – 17 = 0.
Khoảng cách từ điểm M(1; –1) đến đường thẳng ∆ là:
\(d\left( {M,\Delta } \right) = \frac{{\left| {3.1 - 4.\left( { - 1} \right) - 17} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 2\).
Vậy khoảng cách từ điểm M(1; –1) đến đường thẳng ∆ là 2.
Do đó ta chọn phương án C.
Câu 8:
07/11/2024Tọa độ giao điểm của hai đường thẳng 5x – 2y – 29 = 0 và 3x + 4y – 7 = 0 là:
Xem đáp án
Đáp án đúng là: A
Lời giải
Tọa độ giao điểm I của hai đường thẳng đã cho thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}5x - 2y - 29 = 0\\3x + 4y - 7 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = - 2\end{array} \right.\)
Suy ra tọa độ I(5; –2).
Khi đó I ≡ P.
*Phương pháp giải:
Bước 1: Xét phương trình hoành độ giao điểm của d và d’.
ax + b = a’x + b’ (1)
Chú ý:
+ Phương trình (1) vô nghiệm thì d // d’.
+ Phương trình (1) luôn đúng với mọi giá trị x thì d và d’ trùng nhau.
+ Với a ≠ a’, phương trình (1) có nghiệm duy nhất.
(1)
Ta chuyển qua bước 2
Bước 2: Thay x vừa tìm được vào d hoặc d’ để tính y
Ví dụ thay x vào d
Bước 3: Kết luận tọa độ giao điểm.
*Lý thuyết
+ Cho hai đường thẳng d: y = ax + b và d’: y = a’x + b’ với a và a’.
Hai đường thẳng này có duy nhất một điểm chung khi chúng cắt nhau.
Hai đường thẳng không có điểm chung khi chúng song song.
Hai đường thẳng có vô số điểm chung khi chúng trùng nhau.
+ Muốn tìm tọa độ giao điểm hai đường thẳng ta làm như sau (d và d’ cắt nhau)
Xem thêm
Công thức tìm tọa độ giao điểm của hai đường thẳng hay, chi tiết hay nhất - Toán lớp 9
TOP 40 câu Trắc nghiệm Khoảng cách (có đáp án ) – Toán 11