Trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Phần 2) có đáp án (Nhận biết)
-
907 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/11/2024Phương trình nào sau đây là phương trình chính tắc của elip?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
⦁ Phương trình chính tắc của (E) có dạng: x2a2+y2b2=1 (với a > b > 0).
Vì phương trình ở phương án B không có dạng trên nên ta loại phương án B.
⦁ Vì a > b nên a2 > b2.
Phương trình ở phương án A có a2 = 4 < b2 = 25.
Suy ra phương trình ở phương án A không phải là phương trình chính tắc của (E).
⦁ Phương trình ở phương án C có a2 = 49 > b2 = 36.
Suy ra phương trình ở phương án C là phương trình chính tắc của (E).
⦁ Phương trình ở phương án D có a2 = b2 = 49.
Suy ra phương trình ở phương án D không phải là phương trình chính tắc của (E).
Vậy ta chọn phương án C.
*Phương pháp giải:
+ Tiêu cự: F1F2=2c
+ Tâm sai của (E): e=ca<1
+ b2=a2−c2
*Lý thuyết:
- Định nghĩa: Cho hai điểm cố định F1 và F2 và một độ dài không đổi 2a lớn hơn F1F2. Elip là tập hợp các điểm M trong mặt phẳng sao cho F1M+F2M=2a.
- Phương trình chính tắc của elip: Cho elip (E) có các tiêu điểm F1 và F2. Điểm M thuộc elip khi và chỉ khi F1M+F2M=2a. Chọn hệ trục tọa độ Oxy, cho F1(-c; 0) và F2(c; 0). Khi đó ta có:
M (x; y) ∈(E)⇔x2a2+y2b2=1. (1) với b2=a2−c2
Phương trình (1) là phương trình chính tắc của elip.
II. Các công thức
Từ các thông tin đề bài cho, ta tìm a, b dựa vào các công thức:
+ Hai tiêu điểm: F1(-c; 0) và F2(c; 0)
+ Bốn đỉnh: A1(-a; 0), A2(a; 0), B1 (0; -b) và B2(0; b)
+ Độ dài trục lớn: A1A2=2a
+ Độ dài trục nhỏ: B1B2=2b
+ Tiêu cự: F1F2=2c
+ Tâm sai của (E): e=ca<1
+ b2=a2−c2
- Định nghĩa: Cho hai điểm cố định F1 và F2 và một độ dài không đổi 2a lớn hơn F1F2. Elip là tập hợp các điểm M trong mặt phẳng sao cho F1M+F2M=2a.
- Phương trình chính tắc của elip: Cho elip (E) có các tiêu điểm F1 và F2. Điểm M thuộc elip khi và chỉ khi F1M+F2M=2a. Chọn hệ trục tọa độ Oxy, cho F1(-c; 0) và F2(c; 0). Khi đó ta có:
M (x; y) ∈(E)⇔x2a2+y2b2=1. (1) với b2=a2−c2
Phương trình (1) là phương trình chính tắc của elip.
Xem thêm
Công thức phương trình chính tắc của Elip, các dạng bài tập và cách giải
Câu 2:
18/11/2024Phương trình nào sau đây là phương trình chính tắc của hypebol?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải:
Phương trình chính tắc của hypebol (H) có dạng: x2a2−y2b2=1 (với a > 0, b > 0).
Ta thấy phương trình ở phương án B, C, D không có dạng trên nên ta loại phương án B, C, D.
Vậy ta chọn phương án A.
*Phương pháp giải:
+ Tiêu điểm: Tiêu điểm trái F1(−c;0), tiêu điểm phải F2(c;0)
+ Các đỉnh: A1(−a;0),A2(a;0)
+ Trục Ox gọi là trục thực, trục Oy gọi là trục ảo của hypebol.
Khoảng cách 2a giữa hai đỉnh gọi là độ dài trục thực, 2b gọi là độ dài trục ảo.
+ Hypebol gồm hai phần nằm hai bên trục ảo, mỗi phần gọi là nhánh của hypebol
+ Hình chữ nhật tạo bởi các đường thẳng x=±a,y=±b gọi là hình chữ nhật cơ sở. Hai đường thẳng chứa hai đường chéo của hình chữ nhật cơ sở gọi là hai đường tiệm cận của hypebol và có phương trình là y=±bax
+ Tâm sai: e=ca>1
+ M(xM;yM) thuộc (H) thì:
MF1=|a+exM|=|a+caxM|, MF2=|a−exM|=|a−caxM|
*Lý thuyết:
Cho hai điểm cố định F1,F2 với F1F2=2c(c>0) và hằng số a<c.
Hypebol là tập hợp các điểm M thỏa mãn |MF1−MF2|=2a.
Kí hiệu (H)
Ta gọi: F1,F2 là tiêu điểm của (H).
Khoảng cách F1F2=2c là tiêu cự của (H).
II. Phương trình chính tắc của Hypebol
Với F1(−c;0),F2(c;0)
M(x;y)∈(H)⇔x2a2−y2b2=1 với b2=c2−a2 (2)
Phương trình (2) được gọi là phương trình chính tắc của hypebol
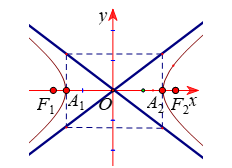
Xem thêm
Hypebol (Lý thuyết, công thức), các dạng bài tập và cách giải
Câu 3:
18/11/2024Phương trình nào sau đây là phương trình chính tắc của parabol?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Lời giải
Phương trình chính tắc của parabol (P) có dạng y2 = 2px (p > 0).
⦁ Ta thấy phương trình ở phương án C, D không có dạng trên nên ta loại phương án C, D.
⦁ Ở phương án A, ta có 2p = –4. Suy ra p = –2 < 0.
Suy ra phương trình ở phương án A không phải phương trình chính tắc của (P).
Vậy ta chọn phương án B.
*Phương pháp giải:
Dựa vào các dữ kiện đề bài ta suy ra các yếu tố sau:
Parabol có tiêu điểm là F(p2;0) và đường chuẩn Δ: x=−p2.
Từ đó tìm được p, thay vào phương trình chính tắc của parabol là y2 = 2px (p > 0).
*Lý thuyết:
Dựa vào các dữ kiện đề bài ta suy ra các yếu tố sau:
Parabol có tiêu điểm là F(p2;0) và đường chuẩn Δ: x=−p2.
Từ đó tìm được p, thay vào phương trình chính tắc của parabol là y2 = 2px (p > 0).
- Khái niệm đường parabol: Một đường parabol là một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
- Phương trình Parabol có dạng: y=ax2+bx+c
- Gọi I là đỉnh của Parabol ta có xI=−b2a; yI=−Δ4a ( trong đó Δ=b2−4ac)
- Phương trình hoành độ giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là:
f(x) = g(x).
- Gốc tọa độ có tọa độ là O(0; 0)
- Trục tung có phương trình: x = 0.
- Trục hoành có phương trình: y = 0
Xem thêm
Câu 4:
14/07/2024Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF1 – MF2| = 2a được gọi là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0).
Đường hypebol là tập hợp các điểm M sao cho |MF1 – MF2| = 2a, trong đó a > 0 và a < c.
Hai điểm F1 và F2 được gọi là hai tiêu điểm của hypebol.
Vậy ta chọn phương án A.
Câu 5:
12/07/2024Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0) và một số a > c. Đường elip là tập hợp các điểm M trong mặt phẳng thỏa mãn:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0).
Đường elip là tập hợp các điểm M trong mặt phẳng so cho MF1 + MF2 = 2a, trong đó a > c.
Hai điểm F1 và F2 được gọi là hai tiêu điểm của elip.
Vậy ta chọn phương án C.
Câu 6:
22/07/2024Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F. Đường parabol là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F.
Đường parabol là tập hợp các điểm M trong mặt phẳng cách đều F và ∆.
Vậy ta chọn phương án B.
Câu 7:
15/07/2024Phương trình đường chuẩn ∆ có dạng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Phương trình đường chuẩn ∆ có dạng: x+p2=0.
Vậy ta chọn phương án D.
Bài thi liên quan
-
Trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Phần 2) có đáp án (Thông hiểu)
-
8 câu hỏi
-
30 phút
-
-
Trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Phần 2) có đáp án (Vận dụng)
-
5 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 6. Ba đường Conic có đáp án (263 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Phần 2) có đáp án (906 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường tròn (Phần 2) có đáp án (930 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Phần 2) có đáp án (858 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Phần 2) có đáp án (685 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳng (Phần 2) có đáp án (545 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 7. Bài tập cuối chương 7 (Phần 2) có đáp án (523 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Phần 2) có đáp án (474 lượt thi)
- Trắc nghiệm Toán 10 Bài ôn tập cuối chương 7 có đáp án (315 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng có đáp án (281 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Phương trình đường thẳng có đáp án (258 lượt thi)
- Trắc nghiệm Toán 10 Bài 2. Biểu thức toạ độ của các phép toán vectơ có đáp án (247 lượt thi)
