Phương trình nào sau đây là phương trình chính tắc của hypebol?

Đáp án đúng là: A

Lời giải:

Phương trình chính tắc của hypebol (H) có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (với a > 0, b > 0).

Ta thấy phương trình ở phương án B, C, D không có dạng trên nên ta loại phương án B, C, D.

Vậy ta chọn phương án A.

*Phương pháp giải:

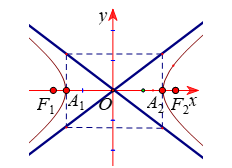
+ Tiêu điểm: Tiêu điểm trái $F_1\left(-c;0\right)$, tiêu điểm phải $F_2\left(c;0\right)$

+ Các đỉnh: $A_1\left(-a;0\right),A_2\left(a;0\right)$

+ Trục $Ox$ gọi là trục thực, trục $Oy$ gọi là trục ảo của hypebol.

Khoảng cách $2a$ giữa hai đỉnh gọi là độ dài trục thực, $2b$ gọi là độ dài trục ảo.

+ Hypebol gồm hai phần nằm hai bên trục ảo, mỗi phần gọi là nhánh của hypebol

+ Hình chữ nhật tạo bởi các đường thẳng $x=\pm a,y=\pm b$ gọi là hình chữ nhật cơ sở. Hai đường thẳng chứa hai đường chéo của hình chữ nhật cơ sở gọi là hai đường tiệm cận của hypebol và có phương trình là $y=\pm {\displaystyle \frac{b}{a}}x$

+ Tâm sai: $e={\displaystyle \frac{c}{a}}>1$

+ $M\left(x_M;y_M\right)$ thuộc $(H)$ thì:

$M{F}_1=\left|a+e{x}_M\right|=\left|a+{\displaystyle \frac{c}{a}}{x}_M\right|,$ $M{F}_2=\left|a-e{x}_M\right|=\left|a-{\displaystyle \frac{c}{a}}{x}_M\right|$

*Lý thuyết:

Cho hai điểm cố định $F_1,F_2$ với $F_1{F}_2=2c\left(c>0\right)$ và hằng số $a<c$.

Hypebol là tập hợp các điểm $M$ thỏa mãn $\left|M{F}_1-M{F}_2\right|=2a$.

Kí hiệu $(H)$

Ta gọi: $F_1,F_2$ là tiêu điểm của $(H).$

Khoảng cách $F_1{F}_2=2c$ là tiêu cự của $(H).$

II. Phương trình chính tắc của Hypebol

Với $F_1\left(-c;0\right),F_2\left(c;0\right)$

$M\left(x;y\right)\in \left(H\right)\iff {\displaystyle \frac{x^2}{a^2}}-{\displaystyle \frac{y^2}{b^2}}=1$ với $b^2=c^2-a^2$ (2)

Phương trình $(2)$ được gọi là phương trình chính tắc của hypebol

Xem thêm

Hypebol (Lý thuyết, công thức), các dạng bài tập và cách giải 

Bài tập Chuyên đề Hypebol có đáp án 

•