Trắc nghiệm Toán 10 Bài 2. Biểu thức toạ độ của các phép toán vectơ có đáp án
-
237 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Cho \[\overrightarrow a \] = (2; – 4), \[\overrightarrow b \]= (– 5; 3). Tìm tọa độ của \[\overrightarrow a \] + \[\overrightarrow b \].
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có : \[\overrightarrow a \] + \[\overrightarrow b \] = (2 + (– 5); – 4 + 3) = (– 3; – 1).
Câu 2:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Ta có : \[\overrightarrow m - \overrightarrow n \] = (3 – (– 1)); – 4 – 2) = (4; – 6).
Câu 3:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có: 2\[\overrightarrow m \]= 2(–1; 2) = (–2; 4)
2\[\overrightarrow m + \overrightarrow n \] = (– 2 + 5); 4 – 7) = (3; – 3).
Câu 4:
22/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Tọa độ điểm I là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x_I} = \frac{{ - 1 + 1}}{2} = 0\\{y_I} = \frac{{1 + 1}}{2} = 1\end{array} \right. \Rightarrow I\left( {0;1} \right)\).
Câu 5:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: 3\[\overrightarrow k \]= 3(5 ; 2) = (15 ; 6) ; 2\[\overrightarrow n \] = 2(10 ; 8) = (20 ; 16)
\[3\overrightarrow k - 2\overrightarrow n \] = (15 – 20 ; 6 – 16) = (– 5; – 10).
Câu 6:
17/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có \[\left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 2; - 1} \right)\\\overrightarrow {AC} = \left( { - 3; - 2} \right)\end{array} \right.\] \[ \Rightarrow \]\[\overrightarrow {AB} - \overrightarrow {AC} \] = (– 2 – (– 3); – 1 – (– 2)) = (1; 1).
Câu 7:
23/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi điểm B có tọa độ (xB ; yB)
Vì I là trung điểm của AB nên ta có :
\[\left\{ \begin{array}{l}{x_I} = \frac{{2 + {x_B}}}{2} = 4\\{y_I} = \frac{{ - 3 + {y_B}}}{2} = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 2.4 - 2 = 6\\{y_I} = 2.7 - ( - 3) = 17\end{array} \right.\] \[ \Rightarrow \] B(6; 17).
Câu 8:
21/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : D
Gọi toạ độ trọng tâm G (\[{x_G}\]; \[{y_G}\]), ta có :
\[\left\{ \begin{array}{l}{x_G} = \frac{{3 + 1 + 5}}{3} = 3\\{y_G} = \frac{{5 + 2 + 2}}{3} = 3\end{array} \right.\] \[ \Rightarrow \]G (3; 3).
Câu 9:
15/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ C(x ; y), ta có:
Vì G là trọng tâm tam giác ABC nên : \[\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right..\] hay C (–6; –3).
Câu 10:
07/12/2024 Xem đáp án
Đáp án đúng là: B
Lời giải
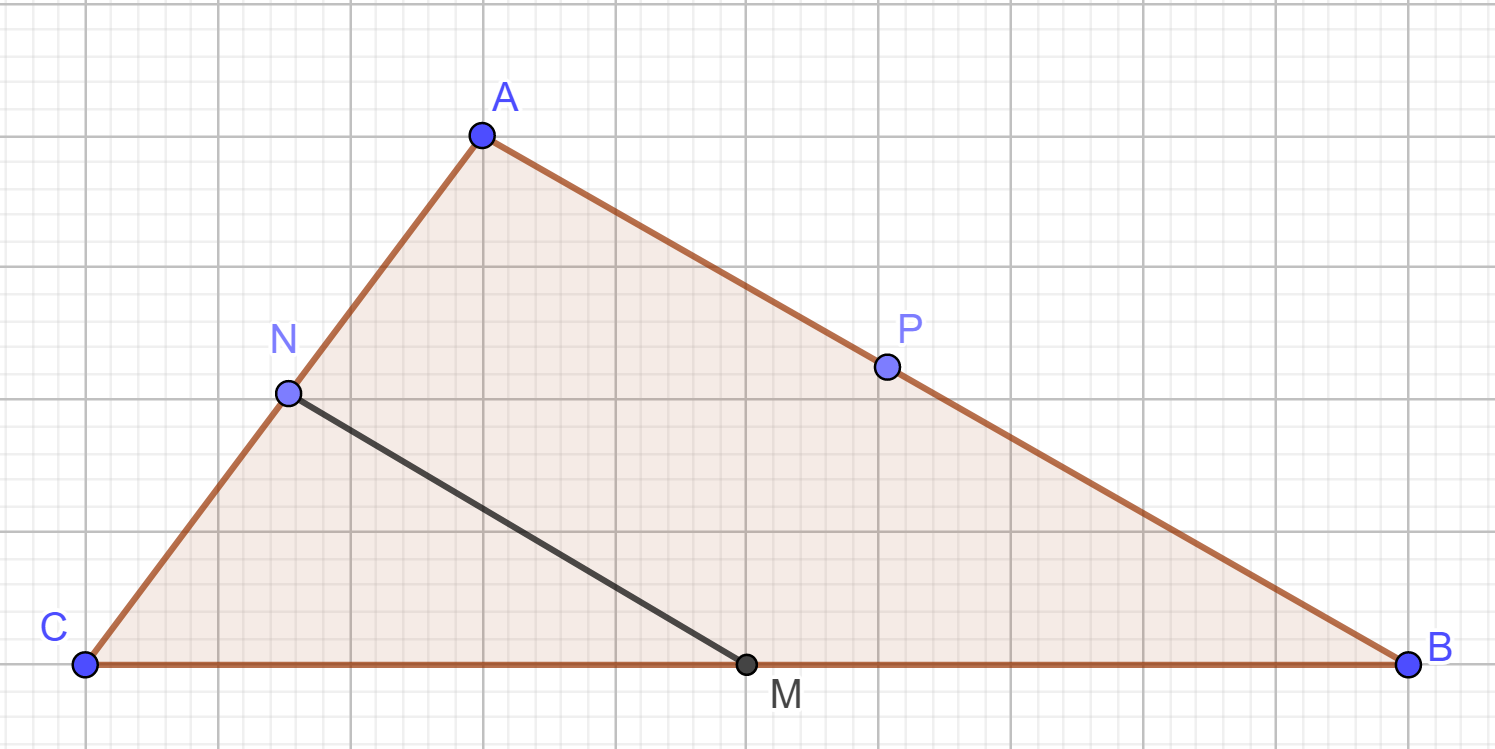
Gọi toạ độ A (x ; y).
Ta có : \[\overrightarrow {PA} \] = (x + 1; y – 6) và \[\overrightarrow {MN} \] = (–2; –7)
Theo tính chất đường trung bình tam giác, ta có:
\[\overrightarrow {MN} \]= \[\frac{1}{2}\]\[\overrightarrow {AB} \] = \[\overrightarrow {PA} \]
Khi đó (1)\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}x + 1 = - 2\\y - 6 = - 7\end{array} \right.\] \[ \Leftrightarrow \]\[\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\]
Hay A (–3; –1).
*Phương pháp giải:
Sử dụng tính chất đường trung bình của tam giác : đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
*Lý thuyết:
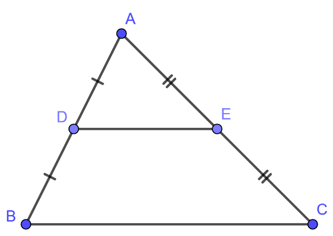
1. Đường trung bình của tam giác là gì?
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
2. Tính chất đường trung bình của tam giác
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.
Ví dụ:
DE là đường trung bình của tam giác ABC, khi đó DE // BC và .
Xem thêm
Lý thuyết Đường trung bình của tam giác (chính xác nhất) và cách giải các dạng bài tập
TOP 40 câu Trắc nghiệm Đường trung bình của tam giác, của hình thang (có đáp án 2) - Ton 8
Câu 11:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Xét tam giác ABC, có :
M là trung điểm AB
N là trung điểm AC
Suy ra MN là đường trung bình tam giác ABC
Theo tính chất đường trung bình, ta có :
\[\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} \] = \[\frac{1}{2}\].(2; –8) = (1; –4).
Câu 12:
18/07/2024Trong hệ tọa độ Oxy cho tam giác ABC có C (–2 ; –4), trọng tâm G (0 ; 4) và trung điểm cạnh BC là M (2 ; 0). Tổng hoành độ của điểm A và B là.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Vì M là trung điểm BC nên ta có : \[\left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_C}\\{y_B} = 2{y_M} - {y_C}\end{array} \right.\]
\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_B} = 2.2 - \left( { - 2} \right) = 6\\{y_B} = 2.0 - \left( { - 4} \right) = 4\end{array} \right.\]\[ \Rightarrow \]B (6; 4).
Vì G là trọng tâm tam giác ABC nên \[\left\{ \begin{array}{l}{x_A} = 3{x_G} - {x_B} - {x_C}\\{y_A} = 3{y_G} - {y_B} - {y_C}\end{array} \right.\]
\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_A} = 3.0 - 6 - ( - 2)\\{y_A} = 3.4 - 4 - ( - 4)\end{array} \right.\]\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_A} = - 4\\{y_A} = 12\end{array} \right.\] hay A (–4 ; 12).
Suy ra \[{x_A} + {x_B}\]= 6 + (–4) = 2.
Câu 13:
12/07/2024Trong hệ tọa độ Oxy cho tam giác ABC có A (– 2 + x ; 2), B (3 ; 5 + 2y), C(x ; 3 – y). Tìm tổng 2x + y với x, y để O (0 ; 0) là trọng tâm tam giác ABC?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Vì O là trọng tâm tam giác ABC nên, ta có : \[\left\{ \begin{array}{l}{x_G} = \frac{{ - 2 + x + 3 + x}}{3} = 0\\{y_G} = \frac{{2 + 5 + 2y + 3 - y}}{3} = 0\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - \frac{1}{2}\\y = - 10\end{array} \right. \Rightarrow 2.x + y = 2.\left( { - \frac{1}{2}} \right) + \left( { - 10} \right) = - 11\].
Câu 14:
20/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ điểm C (x ; y).
Vì G là trọng tâm tam giác ABC nên ta có : \[\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right.\] hay C (–6; –3).
Câu 15:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có : \[\overrightarrow a - \overrightarrow b \] = (–2m; 2) – (2; –7n) = (–2m –2; 2 + 7n)
Mà \[\overrightarrow a - \overrightarrow b \] = (6; – 5)
Nên ta có: \(\left\{ \begin{array}{l} - 2m - 2 = 6\\2 + 7n = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 4\\n = - 1\end{array} \right.\)
Vậy m = – 4 và n = – 1.