Trong mặt phẳng tọa độ Oxy, cặp đường thẳng nào sau đây song song với nhau?

Đáp án đúng là: C

Lời giải:

⦁ d₁ và d₂ có vectơ chỉ phương lần lượt là \({\vec u_1} = \left( {1;2} \right),\,\,{\vec u_2} = \left( {1; - 4} \right)\).

Vì \(\frac{1}{1} \ne \frac{2}{{ - 4}}\) nên \({\vec u_1}\) không cùng phương với \({\vec u_2}\).

Do đó d₁ cắt d₂.

Vì vậy phương án A sai.

⦁ d₃ và d₄ có vectơ chỉ phương lần lượt là \({\vec u_3} = \left( { - 1;2} \right),\,\,{\vec u_4} = \left( { - 1;1} \right)\).

Vì \(\frac{{ - 1}}{{ - 1}} \ne \frac{2}{1}\) nên \({\vec u_3}\) không cùng phương với \({\vec u_4}\).

Do đó d₃ cắt d₄.

Vì vậy phương án B sai.

⦁ d₅ và d₆ có vectơ pháp tuyến lần lượt là \({\vec n_5} = \left( {1; - 1} \right),\,\,{\vec n_6} = \left( {1; - 1} \right)\).

Vì \(\frac{1}{1} = \frac{{ - 1}}{{ - 1}}\) nên \({\vec n_5}\) cùng phương với \({\vec n_6}\) (1)

Chọn M(0; 1) ∈ d₅.

Thế tọa độ M(0; 1) vào phương trình d₆, ta được: 0 – 1 + 10 = 9 ≠ 0.

Suy ra M(0; 1) ∉ d₆    (2)

Từ (1), (2), ta suy ra d₅ // d₆.

Vì vậy phương án C đúng.

⦁ Tọa độ giao điểm của đường thẳng d₇ và d₈ thỏa hệ phương trình: \(\left\{ \begin{array}{l}2x - 5y - 7 = 0\\x - y - 2 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\)

Suy ra hệ phương trình đã cho có nghiệm duy nhất.

Khi đó d₇ cắt d₈.

Vì vậy phương án D sai.

Vậy ta chọn phương án C.

*Phương pháp giải 

Dạng 1: Chứng minh hai đường thẳng song song

Phương pháp giải: Sử dụng một trong các cách sau

- Chứng minh hai đường thẳng đó đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng.

- Chứng minh hai đường thẳng đó cùng song song với một đường thẳng thứ ba.

- Áp dụng định lí về giao tuyến song song.

- Áp dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Dạng 2: Chứng minh bốn điểm đồng phẳng, ba đường thẳng đồng quy trong không gian

a. Chứng minh bốn điểm đồng phẳng

Phương pháp giải:

Chứng minh bốn điểm A, B, C, D đồng phẳng ta tìm hai đường thẳng a, b lần lượt đi qua hai trong bốn điểm trên và chứng minh a, b song song hoặc cắt nhau. Khi đó A, B, C, D thuộc mặt phẳng (a, b).

b. Chứng minh ba đường thẳng đồng quy

Phương pháp giải: 

- Cách 1: Chứng minh đường thẳng thứ nhất đi qua giao điểm của hai đường thẳng còn lại.

- Cách 2: Chứng minh ba đường thẳng đôi một cắt nhau và chúng đôi một nằm trong ba mặt phẳng phân biệt 

Bước 1: Xác định 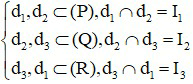  với (P), (Q), (R) phân biệt

Bước 2: Kết luận d₁,d₂,d₃ đồng quy tại I ≡ I₁ ≡ I₂ ≡ I₃  

*Lý thuyết:

1. Vị trí tương đối giữa hai đường thẳng trong không gian

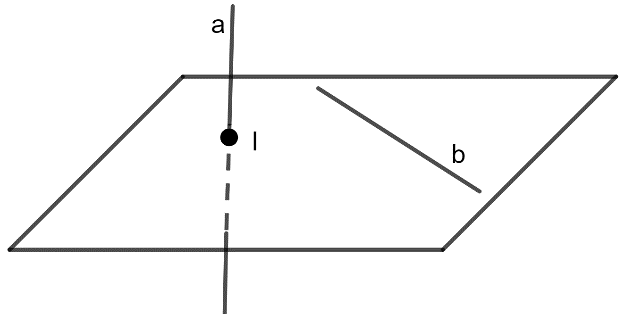
- Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng

- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng. Hai đường thẳng chéo nhau thì không có điểm chung.

 

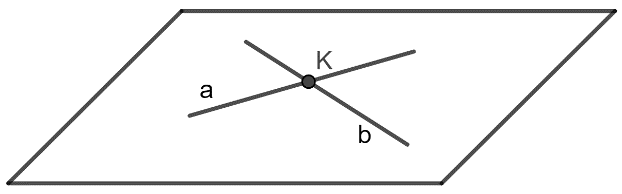
- Hai đường thẳng gọi là cắt nhau nếu chúng đồng phẳng và có một điểm chung

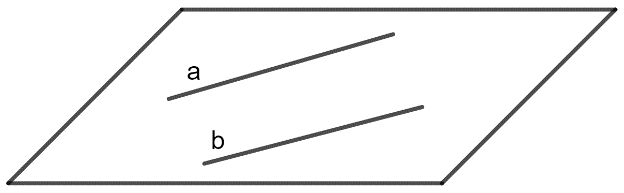
- Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung

- Như vậy, trong không gian, có 4 vị trí tương đối của hai đường thẳng, đó là: song song, trùng nhau, cắt nhau và chéo nhau.

- Khi nhắc đến hai đường thẳng phân biệt, thì ta hiểu là có 3 vị trí tương đối của hai đường thẳng đó (bỏ đi trường hợp trùng nhau).

Xem thêm

Điều kiện để đường thẳng song song với mặt phẳng và cách giải dạng các bài tập (2024) 

TOP 40 câu Trắc nghiệm Hai mặt phẳng song song (có đáp án ) - Toán 11 

 

•