Trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Phần 2) có đáp án (Vận dụng)
-
811 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Phương trình đường thẳng đi qua điểm A(–2; 0) và tạo với đường thẳng d: x + 3y – 3 = 0 một góc 45° là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Gọi ∆ là đường thẳng cần tìm.
Ta có ∆ đi qua điểm A(–2; 0) và có vectơ pháp tuyến \({\vec n_\Delta } = \left( {A;B} \right)\).
Suy ra phương trình tổng quát của ∆ có dạng: A(x + 2) + B(y – 0) = 0.
⇔ Ax + By + 2A = 0.
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {1;3} \right)\).
Theo đề, ta có góc giữa hai đường thẳng ∆ và d bằng 45°.
\( \Leftrightarrow \cos 45^\circ = \frac{{\left| {1.A + 3.B} \right|}}{{\sqrt {{1^2} + {3^2}} .\sqrt {{A^2} + {B^2}} }}\)
\( \Leftrightarrow \left| {A + 3B} \right| = \sqrt {5\left( {{A^2} + {B^2}} \right)} \)
Bình phương hai vế của phương trình trên, ta được: (A + 3B)2 = 5(A2 + B2)
⇔ A2 + 6AB + 9B2 = 5A2 + 5B2
⇔ 4A2 – 6AB – 4B2 = 0 (1)
Trường hợp 1: B = 0.
Ta suy ra 4A2 = 0. Khi đó A = 0.
Vì vậy ta loại trường hợp 1 vì A và B không thể đồng thời bằng 0.
Trường hợp 2: B ≠ 0.
Ta chia 2 vế của phương trình (1) cho B2, ta được: \(4{\left( {\frac{A}{B}} \right)^2} - 6.\left( {\frac{A}{B}} \right) - 4 = 0\).
\( \Leftrightarrow \left[ \begin{array}{l}\frac{A}{B} = 2\\\frac{A}{B} = - \frac{1}{2}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}A = 2B\\ - 2A = B\end{array} \right.\)
Với A = 2B, ta chọn B = 1. Suy ra A = 2.
Khi đó ta có phương trình ∆: 2x + y + 4 = 0.
Với B = –2A, ta chọn A = 1. Suy ra B = –2.
Khi đó ta có phương trình ∆: x – 2y + 2 = 0.
Vậy ta có 2 đường thẳng ∆ thỏa mãn yêu cầu bài toán có phương trình là 2x + y + 4 = 0 hoặc x – 2y + 2 = 0.
Do đó ta chọn phương án B.
Câu 2:
14/07/2024Cho hai điểm A(2; 2), B(5; 1) và đường thẳng ∆: x – 2y + 8 = 0. Lấy điểm C ∈ ∆. Điểm C có hoành độ dương sao cho diện tích tam giác ABC bằng 17. Tọa độ của C là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
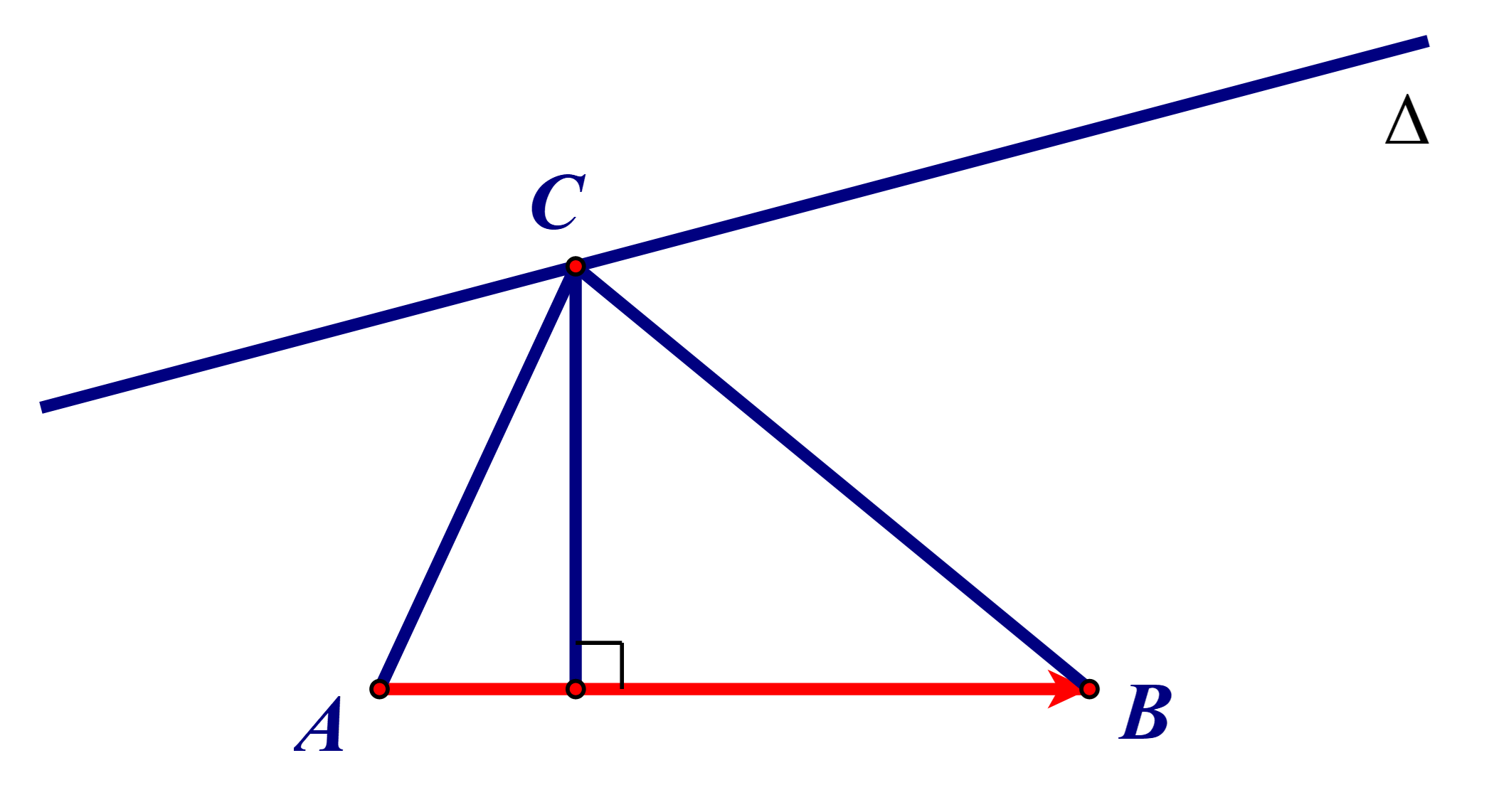
Ta có \(\overrightarrow {AB} = \left( {3; - 1} \right)\). Suy ra \(AB = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \).
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra đường thẳng AB có vectơ pháp tuyến \({\vec n_{AB}} = \left( {1;3} \right)\).
Đường thẳng AB đi qua A(2; 2) và có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra phương trình tổng quát của AB: 1(x – 2) + 3(y – 2) = 0.
⇔ x + 3y – 8 = 0.
Đường thẳng ∆ đi qua điểm M(–8; 0) và có vectơ chỉ phương \({\vec u_\Delta } = \left( {2;1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = - 8 + 2t\\y = t\end{array} \right.\)
Ta có C ∈ ∆. Suy ra tọa độ C(2t – 8; t).
Theo đề, ta có diện tích tam giác ABC bằng 17.
\( \Leftrightarrow \frac{1}{2}d\left( {C,AB} \right).AB = 17\).
\( \Leftrightarrow \frac{1}{2}.\frac{{\left| {2t - 8 + 3t - 8} \right|}}{{\sqrt {{1^2} + {3^2}} }}.\sqrt {10} = 17\)
⇔ |5t – 16| = 34
\( \Leftrightarrow \left[ \begin{array}{l}5t - 16 = 34\\5t - 16 = - 34\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 10\\t = - \frac{{18}}{5}\end{array} \right.\)
Với t = 10, ta có C(12; 10).
Với \(t = - \frac{{18}}{5}\), ta có \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\).
Vậy C(12; 10) hoặc \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 3:
16/07/2024Với giá trị nào của m thì hai đường thẳng d1: 2x – 3y – 10 = 0 và d2: \(\left\{ \begin{array}{l}x = 2 - 3t\\y = 1 - 4mt\end{array} \right.\) vuông góc với nhau?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
⦁ Đường thẳng d1 có vectơ pháp tuyến \({\vec n_1} = \left( {2; - 3} \right)\).
⦁ Đường thẳng d2 có vectơ chỉ phương \({\vec u_2} = \left( { - 3; - 4m} \right)\).
Suy ra đường thẳng d2 có vectơ pháp tuyến \({\vec n_2} = \left( {4m; - 3} \right)\).
Vì d1 ⊥ d2 nên \({\vec n_1} \bot {\vec n_2}\).
\( \Leftrightarrow {\vec n_1}.{\vec n_2} = 0\)
⇔ 2.4m – 3.(–3) = 0
⇔ 8m + 9 = 0
\( \Leftrightarrow m = - \frac{9}{8}\).
Vậy \(m = - \frac{9}{8}\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án C.
Câu 4:
23/07/2024Nếu góc giữa hai đường thẳng d1: x + 2y – 7 = 0 và d2: \(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 2 - mt\end{array} \right.\) bằng 30° thì m gần nhất với giá trị nào sau đây?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
⦁ Đường thẳng d1 có vectơ pháp tuyến \({\vec n_1} = \left( {1;2} \right)\).
Suy ra đường thẳng d1 có vectơ chỉ phương \({\vec u_1} = \left( {2; - 1} \right)\).
⦁ Đường thẳng d2 có vectơ chỉ phương \({\vec u_2} = \left( {3; - m} \right)\).
Theo đề, ta có góc giữa hai đường thẳng d1 và d2 bằng 30°.
⇔ cos(d1, d2) = cos30°
\( \Leftrightarrow \frac{{\left| {2.3 - 1.\left( { - m} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {{\left( { - m} \right)}^2}} }} = \frac{{\sqrt 3 }}{2}\)
\( \Leftrightarrow \frac{{\left| {m + 6} \right|}}{{\sqrt {{m^2} + 9} }} = \frac{{\sqrt {15} }}{2}\)
\( \Leftrightarrow 2\left| {m + 6} \right| = \sqrt {15\left( {{m^2} + 9} \right)} \)
⇔ 4(m + 6)2 = 15(m2 + 9)
⇔ 11m2 – 48m – 9 = 0
\[ \Leftrightarrow \left[ \begin{array}{l}m = \frac{{24 + 15\sqrt 3 }}{{11}} \approx 4,54\\m = \frac{{24 - 15\sqrt 3 }}{{11}} \approx - 0,18\end{array} \right.\]
Vậy m ≈ 4,54 hoặc m ≈ –0,18 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 5:
14/07/2024Hai chiếc ô tô A và B cùng xuất phát từ hai địa điểm, di chuyển theo đường thẳng. Trên màn hình ra đa (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo km), sau khi xuất phát t (giờ) (t ≥ 0), vị trí của ô tô A có tọa độ được xác định bởi công thức \(\left\{ \begin{array}{l}x = 3 - 2t\\y = t\end{array} \right.\), vị trí của ô tô B có tọa độ Q(t; 3 + 2t). Góc giữa hai đường đi của hai ô tô A và B bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là:
Ô tô A di chuyển theo hướng có vectơ chỉ phương \({\vec u_A} = \left( { - 2;1} \right)\).
Ô tô B di chuyển theo hướng có vectơ chỉ phương \({\vec u_B} = \left( {1;2} \right)\).
Gọi α là góc giữa hai đường đi của hai ô tô A và B.
Ta có: \[\cos \alpha = \left| {\cos \left( {{{\vec u}_A};{{\vec u}_B}} \right)} \right| = \frac{{\left| {{{\vec u}_A}.{{\vec u}_B}} \right|}}{{\left| {{{\vec u}_A}} \right|.\left| {{{\vec u}_B}} \right|}}\]
\[ = \frac{{\left| { - 2.1 + 1.2} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + {1^2}} .\sqrt {{1^2} + {2^2}} }} = 0\].
Suy ra α = 90°.
Vậy góc giữa hai đường đi của hai ô tô A và B bằng 90°.
Do đó ta chọn phương án D.