Trắc nghiệm Toán 10 Bài 1: Mệnh đề
-
1487 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Nếu a chia hết cho 9 thì tổng các chữ số của a chia hết cho 9 nên tổng các chữ số của cũng chia hết cho 3. Vậy a chia hết cho 3.
Câu 2:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Theo định nghĩa thì một mệnh đề không thể vừa đúng vừa sai.
Câu 3:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Đáp án D chỉ là một biểu thức, không phải khẳng định.
Câu 4:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Vì các đáp án A, C, D đúng, còn đáp án B dùng ý “hai câu trái ngược nhau” chưa rõ nghĩa.
Câu 6:
23/07/2024Trong các câu sau, có bao nhiêu câu là mệnh đề:
a. Huế là một thành phố của Việt Nam.
b. Sông Hương chảy ngang qua thành phố Huế.
c. Hãy trả lời câu hỏi này!
d. .
e. .
f. Bạn có rỗi tối nay không?
g. .
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Các câu a, b, e là mệnh đề.
Câu 7:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Đáp án B nằm trong bất đẳng thức về độ dài 3 cạnh của một tam giác.
Câu 8:
21/07/2024 Xem đáp án
Xem đáp án
Câu 9:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Đáp án D sai vì B mới là điều kiện cần để có A .
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Phủ định của là
Phủ định của là .
Câu 11:
21/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : D
Lời giải
.
*Phương pháp giải:
Áp dụng lý thuyết mệnh đề
*Lý thuyết:
1. Mệnh đề toán học
• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.
2. Mệnh đề chứa biến
• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.
Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …
3. Phủ định của một mệnh đề
• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là .
Mệnh đề đúng khi P sai, và ngược lại.
4. Mệnh đề kéo theo
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.
Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.
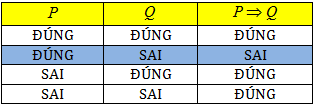
Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…
Xem thêm
Lý thuyết Mệnh đề toán học – Toán 10 Cánh diềuCâu 13:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Với mọi số tự nhiên thì có các trường hợp sau:
chia 3 dư 1.
chia 3 dư 2.
chia 3 dư 2.
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
là tích của 3 số tự nhiên liên tiếp, trong đó, luôn có một số chia hết cho 2 và một số chia hết cho 3 nên nó chia hết cho .
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Tam giác ABC có chưa đủ để nó là tam giác đều.
Câu 17:
23/07/2024Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi!
b) Số 15 là số nguyên tố.
c) Tổng các góc của một tam giác là
d) x là số nguyên dương.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
a) “Cố lên, sắp đói rồi!” không phải là khẳng định. Do đó đây không phải một mệnh đề.
b) “Số 15 là số nguyên tố”: Là một khẳng định. Do đó đây là một mệnh đề.
c) “Tổng các góc của một tam giác là ” là một khẳng định. Do đó đây là một mệnh đề.
d) “ x là số nguyên dương” là một khẳng định nhưng không biết rõ tính đúng sai. Do đó đây là không là một mệnh đề.
Vậy có 2 mệnh đề là b, c.
Câu 19:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
là mệnh đề sai.
Câu 20:
29/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng: A
* Lời giải.
Hai tam giác đồng dạng chưa chắc đã bằng nhau nên mệnh đề A sai.
*Phương pháp giải
Mệnh đề toán học
• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.
*Một số lý thuyết nắm thêm về mệnh đề:
1. Mệnh đề toán học
• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.
2. Mệnh đề chứa biến
• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.
Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …
Ví dụ:
+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến
3. Phủ định của một mệnh đề
• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là ¯¯¯P.
Mệnh đề ¯¯¯P đúng khi P sai, và ngược lại.
Ví dụ:
+ A: “69420 là một số lẻ” là mệnh đề sai.
Mệnh đề phủ định ¯¯¯A: “69420 không phải một số lẻ”, ¯¯¯A là mệnh đề đúng.
Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.
4. Mệnh đề kéo theo
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.
Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…
Ví dụ:
+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.
+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.
Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.
Khi đó ta nói:
P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.
5. Mệnh đề đảo. Mệnh đề tương đương
• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.
Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.
Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:
+ “P tương đương Q”;
+ “P là điều kiện cần và đủ để có Q”;
+ “P khi và chỉ khi Q”;
+ “P nếu và chỉ nếu Q”.
6. Kí hiệu ∀ và ∃
• Kí hiệu ∀ đọc là “với mọi”.
• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).
Ví dụ: Phát biểu các mệnh đề:
+ “∀x∈R,x2+1>0”: Với mọi số thực x thì x2 + 1 luôn lớn hơn 0.
+ “∃x∈N,2x=3”: Tồn tại số tự nhiên x sao cho 2x bằng 3.
• Phủ định của mệnh đề “∀x∈X,P(x)” là mệnh đề “∃x∈X,¯¯¯¯¯¯¯¯P(x)”.
• Phủ định của mệnh đề “∃x∈X,P(x)” là mệnh đề “∀x∈X,¯¯¯¯¯¯¯¯P(x)”.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 21:
29/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải
Xét mệnh đề đảo của đáp án A: “Nếu số nguyên n chia hết cho 5 thì số nguyên n có chữ số tận cùng là 5 ”. Mệnh đề này sai vì số nguyên n cũng có thể có chữ số tận cùng là 0. Xét mệnh đề đảo của đáp án B: “Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”. Mệnh đề này đúng.
*Phương pháp giải
- nắm lại lý thuyết về mệnh đề toán học:
+ Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.
*Lý thuyết cần nắm và dạng bài toán về mệnh đề:
Mệnh đề toán học
• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.
Ví dụ:
+ “Tổng ba góc trong tam giác bằng 1800” là một mệnh đề đúng.
+ “√2√2 là số hữu tỉ” là một mệnh đề sai (vì √2≈1,414213562...√2≈1,414213562...là một số vô tỉ).
Mệnh đề chứa biến
• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.
Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …
Phủ định của một mệnh đề
• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là ¯¯¯P¯¯¯P.
Mệnh đề ¯¯¯P¯¯¯P đúng khi P sai, và ngược lại.
Ví dụ:
+ A: “69420 là một số lẻ” là mệnh đề sai.
Mệnh đề phủ định ¯¯¯A¯¯¯A: “69420 không phải một số lẻ”, ¯¯¯A¯¯¯A là mệnh đề đúng.
Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.
Mệnh đề kéo theo
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.
Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…
Mệnh đề đảo. Mệnh đề tương đương
• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.
Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.
Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:
+ “P tương đương Q”;
+ “P là điều kiện cần và đủ để có Q”;
+ “P khi và chỉ khi Q”;
+ “P nếu và chỉ nếu Q”.
Kí hiệu ∀ và ∃
• Kí hiệu ∀ đọc là “với mọi”.
• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).
Ví dụ: Phát biểu các mệnh đề:
+ “∀x∈R,x2+1>0∀x∈R,x2+1>0”: Với mọi số thực x thì x2 + 1 luôn lớn hơn 0.
+ “∃x∈N,2x=3∃x∈N,2x=3”: Tồn tại số tự nhiên x sao cho 2x bằng 3.
• Phủ định của mệnh đề “∀x∈X,P(x)∀x∈X,P(x)” là mệnh đề “∃x∈X,¯¯¯¯¯¯¯¯P(x)∃x∈X,¯¯¯¯¯¯¯¯P(x)”.
• Phủ định của mệnh đề “∃x∈X,P(x)∃x∈X,P(x)” là mệnh đề “∀x∈X,¯¯¯¯¯¯¯¯P(x)∀x∈X,¯¯¯¯¯¯¯¯P(x)”.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Mệnh đề toán học – Toán 10 Cánh diều
Giải Toán 10 (Cánh diều) Bài tập cuối chương 1 trang 19
TOP 15 câu Trắc nghiệm Mệnh đề toán học (Cánh diều 2024) có đáp án - Toán 10
Câu 22:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phủ định của mệnh đề là mệnh đề . Do đó, phủ định của mệnh đề “Mọi động vật đều di chuyển” là mệnh đề “Có ít nhất một động vật không di chuyển”.
Câu 23:
21/07/2024Phủ định của mệnh đề Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn
là mệnh đề nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phủ định của mệnh đề là mệnh đề . Do đó, phủ định của mệnh đề “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề “Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn”.
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phủ định của mệnh đề “ Số 6 chia hết cho 2 và 3” là mệnh đề: “Số 6 không chia hết cho 2 hoặc 3”.
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Mệnh đề phủ định của mệnh đề P là: : “Tất cả các học sinh khối 10 của trường em đều không biết bơi”.
Có thể bạn quan tâm
- Trắc nghiệm Mệnh đề (có đáp án) (1486 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (721 lượt thi)
- Trắc nghiệm Toán 10 Bài 1(có đáp án): Mệnh đề (312 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Nhận biết) (428 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Thông hiểu) (561 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Vận dụng) (539 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Tổng hợp) (552 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Số gần đúng. Sai số (có đáp án) (2049 lượt thi)
- Trắc nghiệm Tập hợp (có đáp án) (1224 lượt thi)
- 100 câu trắc nghiệm Mệnh đề - Tập hợp cơ bản (859 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Đại số (có đáp án) (730 lượt thi)
- Trắc nghiệm Các tập hợp số (có đáp án) (704 lượt thi)
- Trắc nghiệm Tập hợp có đáp án (Thông hiểu) (624 lượt thi)
- 100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (548 lượt thi)
- Trắc nghiệm Tập hợp có đáp án (Tổng hợp) (480 lượt thi)
- Trắc nghiệm Các tập hợp số có đáp án (Vận dụng) (462 lượt thi)
- Trắc nghiệm Ôn tập chương 1: Mệnh đề - Tập hợp có đáp án (446 lượt thi)
