Trắc nghiệm Mệnh đề có đáp án (Thông hiểu)
Trắc nghiệm Mệnh đề có đáp án (Thông hiểu)
-
554 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Lập mệnh đề phủ định của mệnh đề: “Số 6 chia hết cho cả 2 và 3”:
 Xem đáp án
Xem đáp án
Đáp án C
Phủ định của mệnh đề “ Số 6 chia hết cho 2 và 3” là mệnh đề: “Không phải số 6 chia hết cho cả 2 và 3”, nghĩa là số 6 chỉ chia hết cho một trong hai số 2 và 3 hoặc cũng có thể không chia hết cho số nào.
Ta gọi chung là “Số 6 không chia hết cho 2 hoặc 3”
Câu 2:
14/07/2024Cho các mệnh đề:
(1) “√2 là số hữu tỉ”
(2) “5 không chia hết cho 3”
(3) “ Tam giác có tổng số đo các góc bằng 180°”
(4) “Hình vuông có bốn góc bằng nhau"
Số mệnh đề có mệnh đề phủ định là mệnh đề đúng là:
 Xem đáp án
Xem đáp án
Đáp án D
(1) “ là số hữu tỉ” là mệnh đề sai nên phủ định của nó là một mệnh đề đúng.
(2) “5 không chia hết cho 3” là mệnh đề đúng nên phủ định của nó là mệnh đề sai.
(3) “Tam giác có tổng số đo các góc bằng ” là mệnh đề đúng nên phủ định của nó là mệnh đề sai.
(4) “Hình vuông có bốn góc bằng nhau” là mệnh đề đúng nên mệnh đề phủ định của nó là sai.
Vậy chỉ có 1 mệnh đề mà phủ định của nó là mệnh đề đúng
Câu 3:
21/07/2024Trong các mệnh đề sau, có bao nhiêu mệnh đề mà phủ định của nó là mệnh đề đúng?
a) Hà Nội là một thành phố của Việt Nam
b) Sông Hồng chảy ngang qua thành phố Huế
c) 5 + 19 = 24
d) 6 – 81 = - 75
 Xem đáp án
Xem đáp án
Đáp án A
Mệnh đề câu a: đúng nên phủ định của nó sai.
Mệnh đề câu b: sai nên phủ định của nó đúng.
Mệnh đề câu c: đúng nên phủ định của nó sai.
Mệnh đề câu d: đúng nên phủ định của nó sai.
Vậy có 1 mệnh đề mà phủ định của nó là các mệnh đề đúng
Câu 4:
13/07/2024Cho mệnh đề P: “35 là số có hai chữ số”. Mệnh đề Q nào dưới đây thỏa mãn là mệnh đề sai:
 Xem đáp án
Xem đáp án
Đáp án B
Dễ thấy mệnh đề P: “35 là số có hai chữ số” là mệnh đề đúng nên ta chỉ cần tìm mệnh đề sai trong các đáp án.
Từ các đáp án bài cho ta thấy chỉ có mệnh đề Q: “4 là số nguyên tố” là mệnh đề sai
Câu 5:
21/07/2024Cho mệnh đề P: “5 là số có hai chữ số” và Q là một trong các mệnh đề: “16 chia hết cho 8”; “4 là số nguyên tố”; “ là số vô tỉ”; “4 là số tự nhiên”
Số mệnh đề thỏa mãn là mệnh đề sai là:
 Xem đáp án
Xem đáp án
Đáp án A
Dễ thấy mệnh đề P: “5 là số có hai chữ số” là mệnh đề sai nên mệnh đề Q là mệnh đề nào cũng luôn thỏa mãn P⇒Q là mệnh đề đúng.
Vậy không có mệnh đề nào thỏa mãn bài toán
Câu 6:
23/07/2024Cho tập hợp . Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án D
Các mệnh đề A, B, C đều đúng
Đáp án D sai vì nếu thì nên chưa chắc x thuộc A (chẳng hạn x = - 4)
Câu 8:
23/07/2024Trong các mệnh đề sau đây, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Đáp án A đúng vì với
Đáp án B sai vì nếu x = 0 thì
Đáp án C sai vì
Đáp án D sai vì
Câu 9:
21/07/2024Cho mệnh đề “”. Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó
 Xem đáp án
Xem đáp án
Đáp án D
Phủ định của mệnh đề là
Đây là mệnh đề sai vì với mọi ta có:
Câu 10:
21/07/2024Trong các mệnh đề sau, mệnh đề nào là định lí?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Đáp án A sai vì nếu x = 1 thì nên mệnh đề sai
Đáp án B đúng
Đáp án C sai vì chưa thể suy ra chắc chắn x > 2 mà vẫn có thể xảy ra trường hợp x < -2
Đáp án D sai vì nếu x = - 3 thì mệnh đề sai
Câu 11:
22/07/2024Trong các mệnh đề sau, mệnh đề nào không phải là định lí?
 Xem đáp án
Xem đáp án
Đáp án D
Đáp án A: Trong mặt phẳng, nếu hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song.
Mệnh đề đúng.
Đáp án B: Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau.
Mệnh đề đúng.
Đáp án C: Nếu tứ giác là hình thoi thì nó có hai đường chéo vuông góc với nhau.
Mệnh đề đúng.
Đáp án D: Nếu một số nguyên dương chia hết cho 5 thì tận cùng của nó bằng 5.
Đây là mệnh đề sai vì còn xảy ra trường hợp tận cùng bằng 0
Câu 12:
17/07/2024Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?
 Xem đáp án
Xem đáp án
Đáp án D
Mệnh đề “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau” có thể được phát biểu là:
+) “Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau” nên A đúng.
+) “Điều kiện đủ để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân” nên B đúng, C sai
Câu 13:
20/07/2024Tìm tập hợp tất cả các giá trị thực của x để mệnh đề P: “” là mệnh đề sai:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Do đó với thì mệnh đề đúng, để mệnh đề sai thì
Câu 14:
26/11/2024Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
Mệnh đề kéo theo “ABC là tam giác đều ⇒ Tam giác ABC cân” là mệnh đề đúng, nhưng mệnh đề đảo “Tam giác ABC cân ⇒ABC là tam giác đều” là mệnh đề sai.
Do đó, “ABC là tam giác đều ⇔Tam giác ABC cân” không phải là 2 mệnh đề tương đương
*Phương pháp giải:
Chọn A vì có hầu hết các tam giác cân không là tam giác đều, ví dụ tam giác cân có 1 góc bằng 100 độ
*Lý thuyết
1. Nhận biết tam giác đều
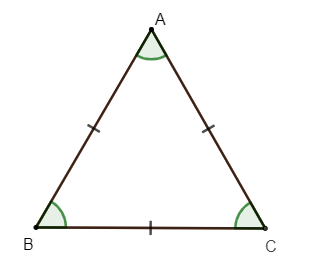
Tam giác đều ABC có
+ Ba cạnh bằng nhau: AB = BC = CA
+ Ba góc ở các đỉnh A, B, C bằng nhau.
Chú ý: Trong hình học nói chung, tam giác nói riêng, các cạnh bằng nhau (hay các góc bằng nhau) thường được chỉ rõ ràng bằng cùng một ký hiệu (xem hình vẽ trên).
2. Vẽ tam giác đều
Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh.
Ví dụ: Dùng thước và compa vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm.
Lời giải:
Để vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm, ta làm như sau:
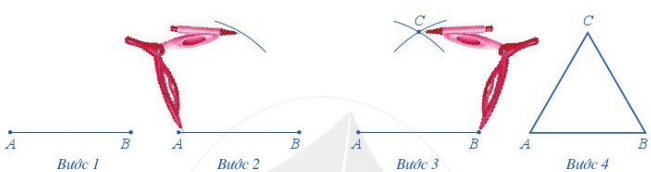
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC
Khi đó ta được tam giác đều ABC có cạnh bằng 3 cm.
Xem thêm
Lý thuyết Tam giác đều. Hình vuông. Lục giác đều chi tiết – Toán lớp 6 Cánh diều
Câu 15:
07/12/2024Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải
Xét mệnh đề đảo của đáp án A: “Nếu số tự nhiên n chia hết cho 3 thì số nguyên n có tổng các chữ số bằng 9”. Mệnh đề này sai vì tổng các chữ số của n phải chia hết cho 9 thì n mới chia hết cho 9.
Xét mệnh đề đảo của đáp án B: “Nếu thì x > y” sai
Vì
Xét mệnh đề đảo của đáp án C: “Nếu t.x = t.y thì x = y” sai với t = 0 ⇒ x,y ∈ R
*Phương pháp giải
- Cho định lí P Q ta nói:
+ "P là điều kiện đủ để có Q" hoặc Q là điều kiện cần để có P"
+ "P là điều kiện cần và đủ để có Q" nếu mệnh đề P Q đúng.
*Một số lý thuyết nắm thêm về mệnh đề:
1. Mệnh đề toán học
• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.
2. Mệnh đề chứa biến
• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.
Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …
Ví dụ:
+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến
3. Phủ định của một mệnh đề
• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là .
Mệnh đề đúng khi P sai, và ngược lại.
Ví dụ:
+ A: “69420 là một số lẻ” là mệnh đề sai.
Mệnh đề phủ định : “69420 không phải một số lẻ”, là mệnh đề đúng.
Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.
4. Mệnh đề kéo theo
• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.
Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.
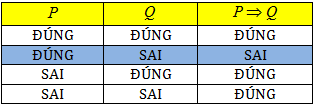
Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…
Ví dụ:
+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.
+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.
Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.
Khi đó ta nói:
P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.
5. Mệnh đề đảo. Mệnh đề tương đương
• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.
Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.
Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:
+ “P tương đương Q”;
+ “P là điều kiện cần và đủ để có Q”;
+ “P khi và chỉ khi Q”;
+ “P nếu và chỉ nếu Q”.
6. Kí hiệu ∀ và ∃
• Kí hiệu ∀ đọc là “với mọi”.
• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).
Ví dụ: Phát biểu các mệnh đề:
+ “”: Với mọi số thực x thì x2 + 1 luôn lớn hơn 0.
+ “”: Tồn tại số tự nhiên x sao cho 2x bằng 3.
• Phủ định của mệnh đề “” là mệnh đề “”.
• Phủ định của mệnh đề “” là mệnh đề “”.
Xem thêm các bài viết hay, chi tiết khác:
Có thể bạn quan tâm
- Trắc nghiệm Mệnh đề (có đáp án) (1474 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (714 lượt thi)
- Trắc nghiệm Toán 10 Bài 1(có đáp án): Mệnh đề (308 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Nhận biết) (420 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Thông hiểu) (553 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Vận dụng) (518 lượt thi)
- Trắc nghiệm Mệnh đề có đáp án (Tổng hợp) (542 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Số gần đúng. Sai số (có đáp án) (2016 lượt thi)
- Trắc nghiệm Tập hợp (có đáp án) (1216 lượt thi)
- 100 câu trắc nghiệm Mệnh đề - Tập hợp cơ bản (850 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Đại số (có đáp án) (722 lượt thi)
- Trắc nghiệm Các tập hợp số (có đáp án) (693 lượt thi)
- Trắc nghiệm Tập hợp có đáp án (Thông hiểu) (614 lượt thi)
- 100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (540 lượt thi)
- Trắc nghiệm Tập hợp có đáp án (Tổng hợp) (469 lượt thi)
- Trắc nghiệm Các tập hợp số có đáp án (Vận dụng) (454 lượt thi)
- Trắc nghiệm Ôn tập chương 1: Mệnh đề - Tập hợp có đáp án (437 lượt thi)
