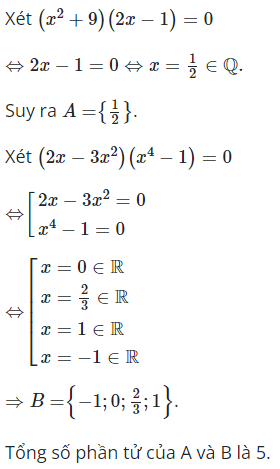Trắc nghiệm Toán 10 Bài 2: Tập hợp
-
1262 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Số tập hợp con khác rỗng của A là 23 (tập).
Câu 2:
23/07/2024Cho tập hợp . Xét các mệnh đề sau đây:
(I): “”.
(II): “”.
(III): “”.
Trong các mệnh đề sau, mệnh đề nào đúng
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
3 là một phần tử của tập hợp A.
là một tập con của tập hợp A. Ký hiệu: .
là một tập con của tập hợp A. Ký hiệu: .
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Vì 3 là số tự nhiên nên ta viết
Câu 4:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
.
Ta có :
Câu 5:
05/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Giải thích:
Lời giải
Xét phương trình:
(Thỏa mãn)
Vậy
*Phương pháp giải:
- Phương trình bậc hai có dạng ()
+ B1:
+B2:vì thì phương trình bậc hai có hai nghiệm phân biệt:
,
+B3: kết luận
*Lý thuyết:
- Cách giải và biện luận phương trình bậc hai:
+ Với
Nếu thì phương trình bậc hai có hai nghiệm phân biệt:
,
Nếu thì phương trình bậc hai có nghiệm kép:
Nếu thì phương trình bậc hai vô nghiệm.
+ Với với
Nếu thì phương trình bậc hai có hai nghiệm phân biệt:
,
Nếu thì phương trình bậc hai có nghiệm kép:
Nếu thì phương trình bậc hai vô nghiệm.
- Đối với các phương trình quy về phương trình bậc hai ta có thể dùng các phép biến đổi như nhân đa thức, quy đồng mẫu số, chuyển vế, lấy nhân tử chung … để đưa phương trình đã cho về dạng ().
Xem thêm:
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
Vậy B = {-1; 6}.
Do đó là sai.
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
Vậy
Câu 8:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Phương trình vô nghiệm nên .
Câu 10:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
.
Ta có :
.
Ta có:
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Xét đáp án A, ta có:
Khi đó A = B.
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Có thể sử dụng máy tính bỏ túi để tính số tập con có 2 phần tử của tập hợp A gồm 4 phần tử là:
Các tập con có 2 phần tử của tập hợp A là:
Câu 13:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Các tập hợp con của A có 3 phần tử là:
{1; 2; 3}, {1; 2; 5}, {1; 3; 5}, {2; 3; 5}.
Vậy có tất cả 4 tập hợp con của A có ba phần tử.
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Các tập hợp con của X có ba phần tử trong đó có chứa là:
Vậy có tất cả 8 tập hợp con của X thỏa mãn điều kiện đầu bài.
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Vì
Để thì
Do đó M = {(0;0)}.
Vậy M có 1 phần tử.
Câu 16:
12/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
* Phương pháp giải:
- Tâp hợp con:
- Tập hợp bằng nhau:
- Nếu tập hợp có n phần tử thì nó có tập hợp con.
* Lời giải:
Số tập con của tập hợp X là :
Số tập con có 2 phần tử của tập hợp X là:
Số tập con của tập hợp X chứa số 1 là: 8
Số tập con có 3 phần tử của tập hợp X là:
* Một số lý thuyết liên quan:
a. Tập hợp
- Tập hợp là một khái niệm cơ bản của toán học, không định nghĩa.
- Giả sử đã cho tập hợp A. Để chỉ a là một phần tử của tập hợp A, ta viết a A (đọc là a thuộc A). Để chỉ a không phải là một phần tử của tập hợp A, ta viết a A (đọc là a không thuộc A).
- Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu .
b. Cách xác định tập hợp
- Có 2 cách xác định tập hợp:
Cách 1: Liệt kê các phần tử của tập hợp.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
- Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.
c. Tập hợp con
- Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B và viết (đọc là A chứa trong B).
- Nếu A không phải là một tập con của B ta viết
- Tính chất:
+)
+)
+)
d. Tập hợp bằng nhau
- Khi và ta nói tập hợp A bằng tập hợp B và viết là A = B.
Xem thêm các bài viết liên quan hay, chi tiết:
Các bài toán về các tập hợp số và cách giải (2024) hay, chi tiết nhất
Phương pháp xác định tập hợp và cách giải bài tập (2024) hay nhất
TOP 20 câu Trắc nghiệm Tập hợp (Kết nối tri thức 2024) có đáp án | Toán 10
Câu 17:
23/07/2024Số phần tử của tập hợp là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Xét
Mà nên .
Vậy tập hợp A có tất cả 7 phần tử.
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có: là đúng.
Ta có: là đúng.
Ta có: là đúng.
Ta có hình thang là tứ giác, do đó . Vậy C sai.
Câu 19:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Xét:
Vậy
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải