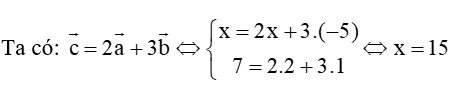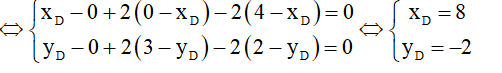Trắc nghiệm Hệ trục tọa độ có đáp án (Thông hiểu)
Trắc nghiệm Hệ trục tọa độ có đáp án (Thông hiểu)
-
375 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho hai điểm A(1;0) và B(0;-2). Tọa độ trung điểm của đoạn thẳng AB là:
 Xem đáp án
Xem đáp án
Chọn đáp án A
I=(xA+xB2;yA+yB2)=(1+02;0+(-2)2)=(12;-1)
Câu 2:
19/07/2024Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B(1;1), C(5;2). Tìm tọa độ trọng tâm G của tam giác ABC?
 Xem đáp án
Xem đáp án
Chọn đáp án D
ta có: 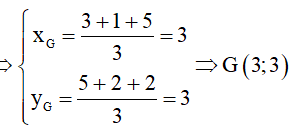
Câu 3:
20/07/2024Cho tam giác ABC có trọng tâm là gốc tọa độ O, hai đỉnh A và B có tọa độ là A (−2; 2); B (3; 5). Tọa độ của đỉnh C là:
 Xem đáp án
Xem đáp án
Chọn đáp án B
ta có:
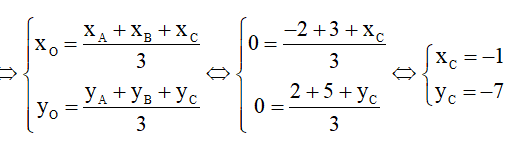
Câu 4:
21/07/2024Trong mặt phẳng Oxy, cho B (5; −4), C (3; 7). Tọa độ của điểm E đối xứng với C qua B là:
 Xem đáp án
Xem đáp án
Chọn đáp án D

Câu 8:
14/07/2024Cho và . Tìm phát biểu sai:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có: nên A đúng
nên D đúng, B sai
Câu 9:
17/07/2024Cho 4 điểm A (1; −2), B (0; 3), C (−3; 4), D (−1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có: 3 điểm A, B, D thẳng hàng
Câu 10:
18/07/2024Trong mặt phẳng Oxy, cho các điểm . Tọa độ điểm M thỏa mãn là:
 Xem đáp án
Xem đáp án
Chọn đáp án C
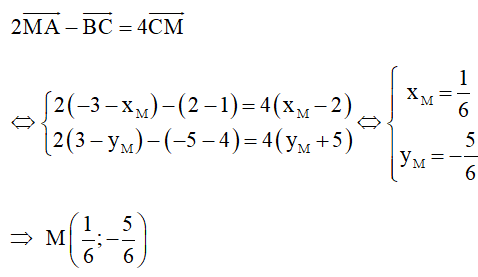
Câu 11:
22/07/2024Trong mặt phẳng tọa độ Oxy cho bốn điểm A (3; −2), B (7; 1), C (0; 1),
D (−8; −5). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 12:
21/07/2024Trong hệ tọa độ Oxy, cho bốn điểm A (2; 1), B (2; −1), C (−2; −3),
D (−2; −1). Xét hai mệnh đề:
(I) ABCD là hình bình hành.
(II) AC cắt BD tại M (0; −1).
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án C

Câu 13:
19/07/2024Trong mặt phẳng Oxy, cho A (−2; 0), B (5; −4), C (−5; 1). Tọa độ điểm D để tứ giác BCAD là hình bình hành là:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có tứ giác BCAD là hình bình hành khi
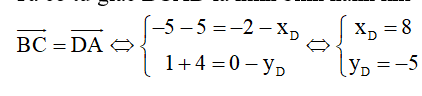
Câu 14:
29/10/2024Cho M (2; 0), N (2; 2), P (−1; 3) lần lượt là trung điểm các cạnh BC, CA, AB của ΔABC. Tọa độ B là:
 Xem đáp án
Xem đáp án
Chọn đáp án C
*Lời giải

*Phương pháp giải
- Ta nhận thấy BPNM là hình bình hành:
áp dụng công thức tọa độ vào hình bình hành ví dụ: XB + XN = XM + XP tương tự với trên tục tung. Từ đó tìm ra XB và YB
* Lý thuyết cần nắm thêm về hệ trục tọa độ:
- Tọa độ của điểm trên trục: Có: −−→OM=k→e. Khi đó số k là tọa độ của điểm M trên trục (O;→e).
- Tọa độ của điểm trong mặt phẳng Oxy: Có M(x;y)⇔−−→OM=x→i+y→j.
- Tọa độ của vectơ trên trục: Trên trục (O;→e) , hai điểm A và B trên trục (O; →e) có tọa độ lần lượt là a và b thì ¯¯¯¯¯¯AB = b – a. Trong đó, ¯¯¯¯¯¯AB là độ dài đại số của vectơ −−→AB đối với trục (O;→e).
- Tọa độ của vectơ trong mặt phẳng Oxy: Với →u=(x;y)⇔→u=x→i+y→j. Với A(xA;yA) và B(xB;yB) ta có: −−→AB=(xB−xA;yB−yA).
- Tọa độ trung điểm
+) Trên trục (O;→i), I là trung điểm của đoạn thẳng AB thì:
xI=xA+xB2
+) Trong mặt phẳng Oxy, I (xI;yI)là trung điểm của đoạn thẳng AB thì:
xI=xA+xB2;yI=yA+yB2
- Tọa độ của trọng tâm G (xG;yG) của tam giác ABC là:
xG=xA+xB+xC3;yG=yA+yB+yC3
- Điều kiện để hai vectơ cùng phương: Hai vectơ →u=(u1;u2) và →v=(v1;v2) với →v≠→0 cùng phương khi và chỉ khi có số k sao cho u1=kv1 và u2=kv2.
- Hai vectơ bằng nhau khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
- Phép toán về tọa độ của vectơ:
Cho →u=(u1;u2) và →v=(v1;v2), khi đó:
→u+→v=(u1+v1;u2+v2)→u−→v=(u1−v1;u2−v2)k.→u=(ku1;ku2), k∈R
Các công thức.
- Độ dài đại số của vectơ −−→AB trên trục: ¯¯¯¯¯¯AB = b – a. ( a, b là tọa độ của A và B trên trục)
- Trong mặt phẳng Oxy:
+) Tọa độ của điểm: M(x;y)⇔−−→OM=x→i+y→j
+) Tọa độ của vectơ:
→u=(x;y)⇔→u=x→i+y→j
−−→AB=(xB−xA;yB−yA) trong đó A(xA;yA) và B(xB;yB)
- Tọa độ trung điểm I của đoạn thẳng AB
+) Trên trục (O;→i) : xI=xA+xB2
+) Trong mặt phẳng Oxy: xI=xA+xB2;yI=yA+yB2
- Tọa độ trọng tâm G của tam giác ABC:
xG=xA+xB+xC3;yG=yA+yB+yC3
- Điều kiện hai vectơ →u=(u1;u2) và →v=(v1;v2) cùng phương: u1v1=u2v2=k
- Hai vectơ bằng nhau: Cho →u=(u1;u2) và →v=(v1;v2) ta có: →u=→v⇔{u1=v1u2=v2
- Phép toán về tọa độ của vectơ: Cho →u=(u1;u2) và →v=(v1;v2)
→u+→v=(u1+v1;u2+v2)→u−→v=(u1−v1;u2−v2)k.→u=(ku1;ku2), k∈R
Xem thêm các bài viết liên quan hay, chi tiết:
Hệ trục tọa độ trong mặt phẳng và cách giải bài tập – Toán lớp 10
Có thể bạn quan tâm
- Trắc nghiệm Hệ trục tọa độ (có đáp án) (869 lượt thi)
- Trắc nghiệm Hệ trục toạ độ có đáp án (375 lượt thi)
- Trắc nghiệm Hệ trục tọa độ có đáp án (Thông hiểu) (374 lượt thi)
- Trắc nghiệm Hệ trục tọa độ có đáp án (Vận dụng) (435 lượt thi)
Các bài thi hot trong chương
- 80 câu trắc nghiệm Vectơ cơ bản (2304 lượt thi)
- 75 câu trắc nghiệm Vectơ nâng cao (2062 lượt thi)
- Trắc nghiệm Các định nghĩa (có đáp án) (881 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ (có đáp án) (859 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Hình học 10 (có đáp án) (843 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết) (838 lượt thi)
- Trắc nghiệm Tích của vectơ với một số (có đáp án) (764 lượt thi)
- Trắc nghiệm Tích của vecto với một số có đáp án (590 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu) (583 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Vận dụng) (577 lượt thi)