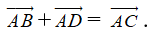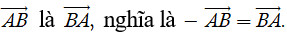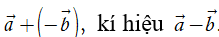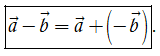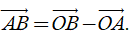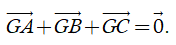Trắc nghiệm Các định nghĩa có đáp án (Vận dụng)
Trắc nghiệm Các định nghĩa có đáp án (Vận dụng)
-
307 lượt thi
-
11 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Cho lục giác đều ABCDEF tâm O. Ba vec tơ bằng vecto ⇀BA là:
 Xem đáp án
Xem đáp án
Ba vectơ bằng vecto là
Đáp án cần chọn là: C
Câu 2:
17/07/2024Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ - không, cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác là
 Xem đáp án
Xem đáp án
Có 6 véc tơ thỏa mãn bài toán, đó là các vectơ:
Đáp án cần chọn là: B
Câu 3:
21/07/2024Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Trong các khẳng định sau, hãy tìm khẳng định sai?
 Xem đáp án
Xem đáp án
Ta có MN là đường trung bình của tam giác ABC.
Suy ra MN = AC hay
Đáp án cần chọn là: D
Câu 4:
10/07/2024Cho hình chữ nhật ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Trong các khẳng định sau, hãy tìm khẳng định sai?
 Xem đáp án
Xem đáp án
Ta thấy, MN//QP//AC và . Hơn nữa cùng hướng nên nên A đúng.
nên B đúng.
MQ//NP//BD và Hơn nữa cùng hướng nên nên C đúng
nên D sai
Đáp án cần chọn là: D
Câu 5:
14/07/2024Cho lục giác đều ABCDEF tâm O. Các vec tơ đối của vecto là:
 Xem đáp án
Xem đáp án
Các vectơ đối của vectơ là:
Đáp án cần chọn là: A
Câu 6:
24/11/2024Cho lục giác đều ABCDEF có tâm O. Đẳng thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:
Đáp án A: đúng.
Đáp án B: đúng vì đều là cạnh của lục giác đều.
Đáp án C: đúng vì cùng hướng và cùng độ dài.
Đáp án D: sai vì hai véc tơ ngược hướng.
*Phương pháp giải
- Nắm vững lại kiến thức về Vectơ để xét từng đáp án
* Lý thuyết cần nắm và một số dạng toán:
– Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.
– Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Chú ý:
+ Vectơ có điểm đầu A và điểm cuối B được kí hiệu là , đọc là vectơ AB.
+ Để vẽ một vectơ, ta vẽ đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối.

+ Vectơ còn được kí hiệu là , , , , …
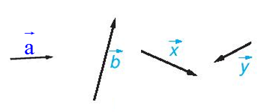
+ Độ dài của vectơ , tương ứng được kí hiệu là , .
Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
+ Hai vectơ và được gọi là bằng nhau, kí hiệu là = , nếu chúng có cùng độ dài và cùng hướng.
Tổng của hai vectơ
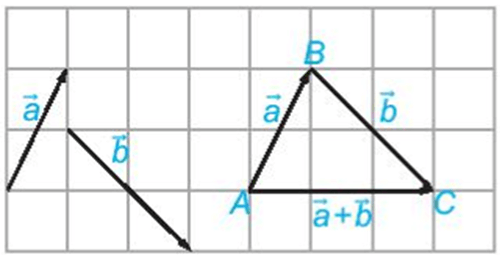
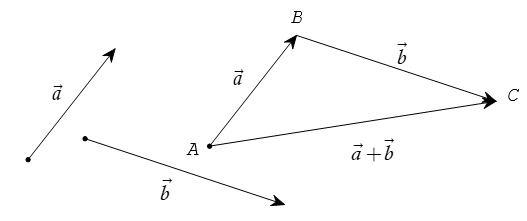
– Cho hai vectơ và . Lấy một điểm A tùy ý và vẽ , . Khi đó vectơ được gọi là tổng của hai vectơ và và được kí hiệu là + .
– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
– Quy tắc ba điểm: Với ba điểm bất kì A, B, C, ta có .
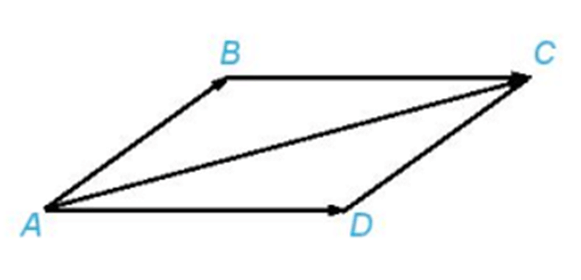
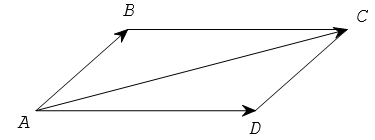
– Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì .
– Với ba vectơ; , , tùy ý :
+ Tính chất giao hoán: + = + ;
+ Tính chất kết hợp: ( + ) + = + ( + );
+ Tính chất của vectơ–không: + = + = .
Chú ý: Do các vectơ ( + ) + và + ( + ) bằng nhau, nên ta còn viết chúng dưới dạng + + và gọi là tổng của ba vectơ , , . Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng dấu ngoặc.
Hiệu của hai vectơ
– Vectơ có cùng độ dài và ngược hướng với vectơ được gọi là vectơ đối của vectơ . Vectơ đối của vectơ kí hiệu là –.
– Vectơ được coi là vectơ đối của chính nó.
– Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng .
– Vectơ + (–) được gọi là hiệu của hai vectơ và và được kí hiệu là – . Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.
– Nếu + = thì – = + (–) = + + (–) = + = .
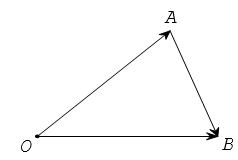
– Quy tắc hiệu: Với ba điểm O, M, N, ta có .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Các khái niệm mở đầu - Toán 10 Kết nối tri thức
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 4 : Vectơ
Câu 7:
23/07/2024Cho tam giác đều ABC với đường cao AH. Đẳng thức nào sau đây đúng:
 Xem đáp án
Xem đáp án
Đáp án A sai do hai vectơ ngược hướng.
Đáp án B đúng vì H là trung điểm BC và
Đáp án C sai vì
Đáp án D sai vì hai véc tơ không cùng phương.
Đáp án cần chọn là: B
Câu 8:
15/07/2024Cho tam giác ABC đều cạnh a. Gọi H là trung điểm BC. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Tam giác ABC đều cạnh a, trung điểm H của BC nên AC = AB = BC = a và
Tam giác ABH vuông tại H nên
Do đó nên A đúng.
nên B đúng.
nên C sai.
nên D đúng.
Đáp án cần chọn là: C
Câu 9:
23/07/2024Cho tam giác ABC với trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có: BD là đường kính
Ta có:
Ta lại có:
Từ (1) và (2) => tứ giác HADC là hình bình hành
Đáp án cần chọn là: C
Câu 10:
27/11/2024Cho và một điểm C. Có bao nhiêu điểm D thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án đúng: D
* Lời giải:
Ta có:
Nghĩa là ta cần đi tìm các điểm D thỏa mãn cách D một khoảng bằng độ dài đoạn AB.
Suy ra tập hợp điểm D là đường tròn tâm C bán kính AB.
Vậy có vô số điểm D thỏa mãn
* Phương pháp giải:
Sử dụng định nghĩa hai vecto bằng nhau.
*Một số lý thuyết và dạng bài tập về vectơ:
Hai vectơ , bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu:
Nhận xét:
– Hai vectơ và được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu = .
– Khi cho trước vectơ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho
Tổng của hai vectơ
Định nghĩa. Cho hai vectơ 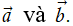
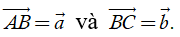
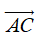
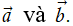
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì
Tính chất của phép cộng các vectơ
Với ba vectơ 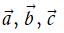
• 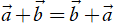
• 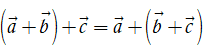
• 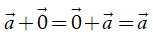
Hiệu của hai vectơ
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của
Đặc biệt, vectơ đối của vectơ 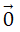
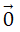
Định nghĩa hiệu của hai vectơ
Định nghĩa. Cho hai vectơ 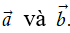
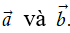
Như vậy
Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có
Chú ý
1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.
2) Với ba điểm tùy ý A, B, C ta luôn có
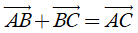
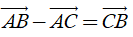
Áp dụng
a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi
b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khái niệm vectơ – Toán 10 Cánh diềuCâu 11:
18/07/2024Cho hình thoi ABCD cạnh a và . Đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Tam giác ABD có AB = AD = a và nên là tam giác ABC đều cạnh a.
Do đó BD = AB = AD = a
Ngoài ra các đáp án A, C sai vì mỗi cặp véc tơ đều không cùng phương.
Đáp án D sai vì chứ không phải
Đáp án cần chọn là: B
Có thể bạn quan tâm
- Trắc nghiệm Các định nghĩa (có đáp án) (853 lượt thi)
- Trắc nghiệm Các định nghĩa vecto có đáp án (437 lượt thi)
- Trắc nghiệm Các định nghĩa có đáp án (Nhận biết) (289 lượt thi)
- Trắc nghiệm Các định nghĩa có đáp án (Thông hiểu) (258 lượt thi)
- Trắc nghiệm Các định nghĩa có đáp án (Vận dụng) (306 lượt thi)
Các bài thi hot trong chương
- 80 câu trắc nghiệm Vectơ cơ bản (2217 lượt thi)
- 75 câu trắc nghiệm Vectơ nâng cao (1991 lượt thi)
- Trắc nghiệm Hệ trục tọa độ (có đáp án) (845 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ (có đáp án) (819 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết) (811 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Hình học 10 (có đáp án) (784 lượt thi)
- Trắc nghiệm Tích của vectơ với một số (có đáp án) (728 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu) (560 lượt thi)
- Trắc nghiệm Tích của vecto với một số có đáp án (557 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Vận dụng) (553 lượt thi)