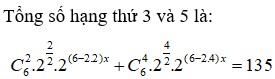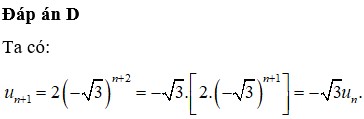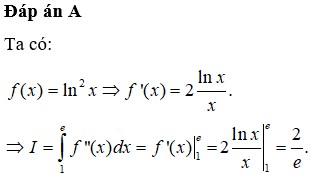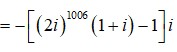49 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử THPT quốc gia môn Toán cực hay có lời giải chi tiết (Đề số 18)

Câu 1:

21/07/2024

Bảng biến thiên dưới đây là của hàm số nào

A. $y = 4 x^{3} - x$

B. $y = - 4 x^{3} - x$

C. $y = - 4 x^{3} + x$

D. $y = 4 x^{3} + x$

Xem đáp án

Câu 2:

21/07/2024

Tìm nguyên hàm của hàm số $f (x) = x + \frac{1}{x}$

A. $\int f (x) d x = 1 - \frac{1}{x^{2}} + C$

B. $\int f (x) d x = \frac{x^{2}}{2} + C$

C. $\int f (x) d x = \frac{x^{2}}{2} + \ln x + C$

D. $\int f (x) d x = \frac{x^{2}}{2} + \ln |x| + C$

Xem đáp án

Câu 3:

21/07/2024

Tìm nghiệm phức của phương trình $z^{2} - 3 z + 4 = 0$

A. $z = \frac{3 \pm i \sqrt{7}}{2}$

B. $z = \frac{7 \pm i \sqrt{3}}{2}$

C. $z = \frac{5 \pm i \sqrt{3}}{2}$

D. $z = \frac{1 \pm i \sqrt{5}}{2}$

Xem đáp án

Câu 4:

21/07/2024

Cho khối lăng trụ ABCD. A'B'C'D'có đáy ABCD là hình vuông cạnh a và có thể tích bằng $3 a^{2}$ . Tính chiều cao h của khối lăng trụ ABCD. A'B'C'D'.

A. h=5a

B. h=8a

C. h=4a

D. h=3a

Xem đáp án

Câu 5:

21/07/2024

Cho một mặt cầu có diện tích bằng $\frac{8 {πa}^{2}}{3}$ . Tính bán kính mặt cầu.

A. $\frac{a \sqrt{6}}{3}$

B. $\frac{a \sqrt{6}}{5}$

C. $\frac{a \sqrt{6}}{7}$

D. $\frac{a \sqrt{6}}{15}$

Xem đáp án

Câu 6:

21/07/2024

Tìm số phức liên hợp của số phức z=(2-3i)(1+i)

A. $\bar{z} = 5 + i$

B. $\bar{z} = 5 - i$

C. $\bar{z} = - 5 + i$

D. $\bar{z} = - 5 - i$

Xem đáp án

Câu 7:

21/07/2024

Số nào trong các số sau là số thần ảo

A. $(\sqrt{2} + 3 i) + (\sqrt{2} - 3 i)$

B. $(\sqrt{2} + 3 i) . (\sqrt{2} - 3 i)$

C. ${(2 + 2 i)}^{2}$

D. $\frac{2 + 3 i}{2 - 3 i}$

Xem đáp án

Câu 8:

21/07/2024

Hình vẽ bên là đồ thị của bốn hàm số $y = {\sqrt{2}}^{x}, y = \frac{1}{4^{x}}, y = {(\frac{1}{\sqrt{2}})}^{x}, y = 5^{x}$

Mệnh đề nào dưới đây đúng

A. $(C_{1}), (C_{2}), (C_{3}), (C_{4}) l ầ n l ư ợ t l à đ ồ t h ị c ủ a y = 5^{x}, y = {\sqrt{2}}^{x}, y = {(\frac{1}{\sqrt{2}})}^{x}, y = \frac{1}{4^{x}}$

B. $(C_{1}), (C_{2}), (C_{3}), (C_{4}) l ầ n l ư ợ t l à đ ồ t h ị c ủ a y = {(\frac{1}{\sqrt{2}})}^{x}, y = \frac{1}{4^{x}}, y = 5^{x}, y = {\sqrt{2}}^{x}$

C. $(C_{1}), (C_{2}), (C_{3}), (C_{4}) l ầ n l ư ợ t l à đ ồ t h ị c ủ a y = \frac{1}{4^{x}}, y = 5^{x}, y = {(\frac{1}{\sqrt{2}})}^{x}, y = {\sqrt{2}}^{x}$

D. $(C_{1}), (C_{2}), (C_{3}), (C_{4}) l ầ n l ư ợ t l à đ ồ t h ị c ủ a y = {\sqrt{2}}^{x} . y = \frac{1}{4^{x}}, y = {(\frac{1}{\sqrt{2}})}^{x}, y = 5^{x}$

Xem đáp án

Câu 9:

21/07/2024

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tính $I = \int_{0}^{4} f' (x - 2) d x + \int_{0}^{2} f' (x + 2) d x$

A. 10

B. -2

C. 2

D. 6

Xem đáp án

Câu 10:

21/07/2024

Tìm giá trị cực tiểu $y_{C T}$ của hàm số $y = \frac{x^{5}}{5} - \frac{x^{3}}{3} + 2$

A. $2 \frac{2}{15}$

B. $1 \frac{13}{15}$

C. $1 \frac{2}{15}$

D. $2 \frac{13}{15}$

Xem đáp án

Câu 11:

21/07/2024

Biết điểm A(1; -6) là điểm cực trị của đồ thị hàm số $y = 2 x^{3} + m x^{2} + n x + 1$ . Tìm m và n

A. m=3, n=-12

B. m=-3, n=12

C. m=12, n=3

D. m=-12, n=-3

Xem đáp án

Câu 12:

21/07/2024

Cho hàm số $y = 2 x^{3} - 3 x^{2} + 1$ có đồ thị (C). Tìm điểm M thuộc (C) sao cho hệ số góc của tiếp tuyến của (C) tại M nhỏ nhất

A. $M (0; 1)$

B. $M (1; 0)$

C. $M (- \frac{1}{2}; 0)$

D. $M (\frac{1}{2}; \frac{1}{2})$

Xem đáp án

Câu 13:

21/07/2024

Một hộp chứa 9 quả cầu gồm 7 quả màu xanh và 2 quả màu đỏ. Chọn ngẫu nhiên đồng thời 5 quả từ hộp đó. Xác suất để 5 quả chọn ra có đúng 1 quả màu đỏ bằng

A. $\frac{5}{9}$

B. $\frac{5}{18}$

C. $\frac{1}{9}$

D. $\frac{2}{9}$

Xem đáp án

Câu 14:

22/07/2024

Tìm nghiệm của phương trình $2^{x} + 2^{x + 1} + 2^{x + 2} = 21$

A. $x = \log_{3} 2$

B. $x = \log_{2} 3$

C. $x = 2$

D. $x = 3$

Xem đáp án

Câu 15:

21/07/2024

Bất phương trình $\log_{\frac{1}{3}} (3 x - 5) > \log_{\frac{1}{5}} (x + 1)$ có điều kiện xác đinh là $x \in S$ , khi đó

A. $S = (\frac{5}{3}; + \infty)$

B. $S = (3; + \infty)$

C. $S = (\frac{5}{3}; 3)$

D. $S = (3; 5)$

Xem đáp án

Câu 16:

23/07/2024

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình $(m^{2} + 2) c o s^{2} x - 2 m \sin 2 x + 1 = 0$ có nghiệm

A. 3

B. 7

C. 6

D. 4

Xem đáp án

Câu 17:

22/07/2024

Gọi $x_{1}, x_{2}$ là hai giá trị của x thỏa mãn. Tổng của số hạng thứ 3 và thứ 5 trong khai triển $(2$ ^x+2^12-x)nbằng 135. Tính T= $x_{1} + x_{2}$ , biết rằng $C_{n}^{n - 2} + C_{n}^{n - 1} + C_{n}^{n} = 22$

A. $- \frac{1}{2}$

B. $3$

C. $\frac{1}{2}$

D. $- 3$

Xem đáp án

Câu 18:

21/07/2024

Cho hàm số y=f(x) liên tục, có đạo hàm f'(x) với mọi x và đồ thị của hàm số y=f'(x) là đường cong cho ở hình vẽ bên. Mệnh đề nào dưới đây đúng

A. $H à m s ố f (x) đ ồ n g b i ế n t r ê n k h o ả n g (- \infty; 2) v à (3; + \infty)$

b. $H à m s ố f (x) n g h ị c h b i ế n t r ê n k h o ả n g (- \infty; 2) v à (3; + \infty)$

C. $H à m s ố f (x) đ ồ n g b i ế n t r ê n k h o ả n g (2; 3)$

D. $H à m s ố f (x) n g h ị c h b i ế n t r ê n k h o ả n g (0; 2)$

Xem đáp án

Câu 19:

21/07/2024

Biết $\int_{0}^{1} (\frac{1}{2 x + 1} - \frac{1}{3 x + 1}) d x = \frac{1}{6} \ln \frac{a}{b}$ trong đó a,b là 2 số nguyên dương và a/b là phân số tối giản. Mệnh đề nào dưới đây sai

A. $a - b = 11$

B. $\frac{a}{9} + \frac{b}{4} = 7$

C. $a + b < 22$

D. $\sqrt[3]{a} + \sqrt{b} = 7$

Xem đáp án

Câu 20:

21/07/2024

Kí hiệu (H) là hình phẳng giới hạn bởi các đường $y = (4 - x^{2})$ , y=0. Tính thể tích V của khối tròn xoay thu được khi quay (H) quanh trục Ox

A. $V = 2 π$

B. $V = \frac{71 π}{82}$

C. $V = \frac{512 π}{15}$

D. $V = \frac{8 π}{3}$

Xem đáp án

Câu 21:

21/07/2024

Tính mô đun của số phức $z = \frac{{(2 + i)}^{2}}{i}$

A. 5

B. 10

C. 15

D. 13

Xem đáp án

Câu 22:

21/07/2024

Cho số phức z thỏa mãn $2 z = i (\bar{z} + 3)$ . Điểm nào dưới đây là điểm biểu diễn số phức z?

A. (-1; -2)

B. (2; 1)

C. (-2; -1)

D. (1; 2)

Xem đáp án

Câu 23:

21/07/2024

Cho hình lăng trụ đứng ABC. A'B'C' có AC=a, BC=2a, $\hat{A C B} = 120 °$ . Tính khoảng cách từ điểm C tới mặt phẳng (ABB'A')

A. $\frac{a \sqrt{12}}{7}$

B. $\frac{a \sqrt{21}}{7}$

C. $\frac{a \sqrt{7}}{21}$

D. $\frac{a \sqrt{7}}{12}$

Xem đáp án

Câu 24:

21/07/2024

Cho hình chóp SABC có đáy là tam giác vuông cân tại B, AB=a, SA vuông góc với đáy, $S A = a \sqrt{6}$ . Tính Sin của góc giữa đường thẳng AC và mặt phẳng (SBC).

A. $\frac{\sqrt{3}}{7}$

B. $\frac{\sqrt{6}}{7}$

C. $\sqrt{\frac{3}{7}}$

D. $\sqrt{\frac{6}{7}}$

Xem đáp án

Câu 25:

21/07/2024

Cho cấp số nhân $(u_{n})$ có $u_{n} = 2 {(- \sqrt{3})}^{n + 1}$ . Tìm công bội q của cấp số nhân đó

A. $q = 6 (\sqrt{3} + 1)$

B. $q = - 6 (\sqrt{3} + 1)$

C. $q = \sqrt{3}$

D. $q = - \sqrt{3}$

Xem đáp án

Câu 26:

21/07/2024

Gọi d là đường thẳng giao tuyến của hai mặt phẳng (P): x+2y-5z+1=0 và (Q): 2x-y+3z-1=0. Tính véc tơ chỉ phương $\vec{u}$ của d

A. $\vec{u} = (1; - 13; - 5)$

B. $\vec{u} = (1; 13; - 5)$

C. $\vec{u} = (1; - 13; 5)$

D. $\vec{u} = (1; 13; 5)$

Xem đáp án

Câu 27:

21/07/2024

Trong không gian Oxyz, cho 2 điểm A(3; 2; 1), B(-2; 4; 2). Tìm tọa độ của điểm M thuộc trục hoành và cách đều 2 điểm A,B

A. $M (- 1; 0; 0)$

B. $M (- \frac{1}{2}; 0; 0)$

C. $M (1; 0; 0)$

D. $M (\frac{1}{2}; 0; 0)$

Xem đáp án

Câu 28:

21/07/2024

Trong không gian Oxyz, cho 2 điểm A(2; 1; 4), B(-4; 3; -2) và cho đường thẳng $d : \frac{x + 3}{1} = \frac{y - 2}{1} = \frac{z + 7}{2}$ . Tìm tọa độ điểm M thuộc d sao cho OM vuông góc với AB

A. M(-3; 2; -7)

B. M(-6; 2; -6)

C. M(1; 6; 1)

D. M(-1; -6; -1)

Xem đáp án

Câu 29:

21/07/2024

Tìm m để 2 đường thẳng $d_{1} : \{\begin{cases} \begin{array}{l} x = - 1 + t \\ y = 1 - t \end{array} \\ z = 1 + 2 t \end{cases}$ , $d_{2} : \{\begin{cases} \begin{array}{l} x = 1 + s \\ y = - 1 + m s \end{array} \\ z = 3 + 4 s \end{cases}$ chéo nhau.

A. $m = - 1$

B. $m k h á c - 1$

C. $m = 2$

D. $m k h á c 2$

Xem đáp án

Câu 30:

27/11/2024

Cho $x^{2}, \frac{1}{2} y^{2}$ theo thứ tự lập thành một cấp số cộng. Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức $\sqrt{3} x y + y^{2}$ . Tính S=M+m

A. S=1

B. S=2

C. S=3

D. S=5

Xem đáp án

Đáp án đúng là A

Lời giải

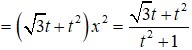
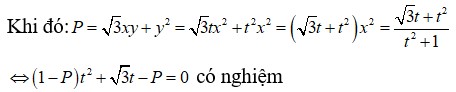
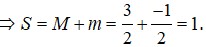
*Phương pháp giải:

1. lập cấp số cộng

2.Tìm max min

*Lý thuyết:

+ Điều kiện để ba số a; b; c lập thành cấp số cộng là c − b = b − a hay a + c= 2b.

+ Điều kiện để dãy số (u_n) là cấp số cộng là với ∀n ∈ N* thì: u_n+1 − u_n là hằng số ( không phụ thuộc vào n) .

- Định nghĩa: Cho hàm số $y = f (x)$ xác định trên tập D

a. Số M được gọi là giá trị lớn nhất của hàm số $y = f (x)$ trên D nếu $f (x) \leq M \forall x \in D$ và tồn tại $x_{0} \in D : f (x_{0}) = M$

- Kí hiệu là: $M = \max_{D} f (x)$

b. Số m được gọi là giá trị nhỏ nhất của hàm số $y = f (x)$ trên D nếu $f (x) \geq M \forall x \in D$ và tồn tại $x_{0} \in D : f (x_{0}) = m$

- Kí hiệu là: $m = \min_{D} f (x)$

2. Các bước tìm GTLN - GTNN của hàm số trên D hoặc trên một khoảng xác định.

- Tìm TXĐ: D

- Tính $y'$ . Tìm những điểm mà $y' = 0$ và $y'$ không xác định

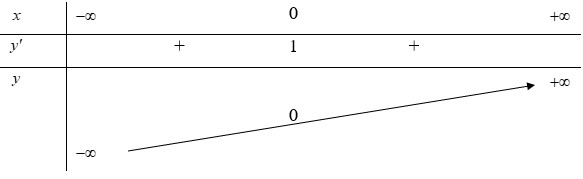
- Lập bảng biến thiên

- Dựa vào bảng biến thiên và kết luận GTLN; GTNN

- Lưu ý: GTLN, GTNN của hàm số phải là số hữu hạn

+ Trong một vài TH (thường là hàm phân thức) GTLN, GTNN hữu hạn nhưng đạt tại $x = \pm \infty$ . Khi đó ta cũng kết luận là hàm số không có GTLN (GTNN).

3. Cách tính GTLN và GTNN trên một đoạn

a. Định lí: Mọi hàm số liên tục trên một đoạn đều có GTLN và GTNN trên đoạn đó.

b. Quy tắc tìm GTLN, GTNN trên đoạn [a,b]

- Tìm các điểm $x_{1}, x_{2}, ... x_{n}$ trên khoảng $(a; b)$ mà tại đó $f' (x) = 0$ hoặc $f' (x)$ không xác định

- Tính $f (a), f (x_{1}), f (x_{2}), ... f (x_{n}), f (b)$ .

- Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.

- Kết luận: $\max_{[a; b]} f (x) = M$ và $\min_{[a; b]} f (x) = m$

- Chú ý: Đối với hàm phân thức $y = \frac{a x + b}{c x + d}$ . Khi tìm GTLN và GTNN của hàm này trên đoạn $[m; n]$ .

+) Nếu $- \frac{d}{c} \in [m; n]$ thì hàm số không có GTLN và GTNN

+) Nếu $- \frac{d}{c} \notin [m; n]$ thì GTLN và GTNN sẽ đạt tại các đầu mút.

Xem thêm

Công thức tính Cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất

Công thức tính GTNN - GTLN của hàm số chi tiết nhất – Toán 12

Câu 31:

21/07/2024

Cho hàm số y=f(x) xác định trên $R / \{2\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau

Tìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m=0 có hai nghiệm.

A. $(- \infty; - 2) \cup (6; + \infty)$

B. $(- \infty; - 6) \cup (- 2; + \infty)$

C. $(2; 6)$

D. $(- 6; - 2)$

Xem đáp án

Câu 32:

21/07/2024

Cho hình chóp SABC có đáy là tam giác vuông cân tại A, $B C = a \sqrt{2}$ , các tam giác SAB và SAC là tam giác đều. Tính Cô sin của góc giữa hai mặt phẳng (SAB) và (SAC).

A. $\frac{1}{3}$

B. $\frac{1}{5}$

C. $\frac{1}{7}$

D. $\frac{3}{8}$

Xem đáp án

Câu 33:

21/07/2024

Một loại cây xanh trong quá trình quang hợp sẽ nhận một lượng nhỏ cacbon X. Khi một bộ phận của một cái cây nào đó bị chết thì hiện tượng quang hợp cũng ngưng và nó sẽ không nhận thêm cacbon X nữa. Lượng cacbon X của bộ phận đó sẽ phân hủy và chuyển hóa thành nitơ X. Biết rằng, nếu gọi P(t) là số phần trăm cacbon X còn lại trong một bộ phận của một cái cây sinh trưởng từ t năm trước đây thì P(t) được tính theo công thức $P (t) = 100.0, 5^{\frac{t}{5750}} %$ . Phân tích một mẩu gỗ từ một công trình kiến trúc cổ, người ta thấy lượng cacbon X còn lại trong mẩu gỗ đó là 65%. Hãy xác định niên đại của mẩu gỗ đó

A. 3574 năm

B. 3547 năm

C. 3457 năm

D. 3754 năm

Xem đáp án

Câu 34:

21/07/2024

Gọi M là tập tất cả các số tự nhiên có 6 chữ số khác nhau được tạo ra từ các chữ số 0,1,2,3,4,5. Chọn ngẫu nhiên một số từ M, tính xác xuất để số đó là số có chữ số 2 đứng cạnh chữ số 3

A. $\frac{7}{25}$

B. $\frac{8}{25}$

C. $\frac{11}{25}$

D. $\frac{5}{9}$

Xem đáp án

Câu 35:

23/07/2024

Tìm m đề phương trình $2 \log_{4} (2 x^{2} - x + 2 m - 4 m^{2}) + \log_{\frac{1}{2}} (x^{2} + m x - 2 m^{2})$ có 2 nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn ${x_{1}}^{2} + {x_{2}}^{2} > 1$

A. $(- 1; 0) \cup (\frac{2}{5}; \frac{1}{2})$

B. $(- 1; 0)$

C. $(- 1; 0) \cup (\frac{5}{2}; 4)$

D. $(\frac{2}{5}; \frac{1}{2})$

Xem đáp án

Câu 36:

21/07/2024

Tìm n để $\int_{0}^{\frac{π}{3}} c o s^{n} \sin x d x = \frac{15}{64}$

A. n=1

B. n=2

C. n=3

D. n=4

Xem đáp án

Câu 37:

21/07/2024

Cho $f (x) = \ln^{2} x$ . Tính $I = \int_{1}^{e} f'' (x) d x$

A. $I = \frac{2}{e}$

B. $I = e - 1$

C. $I = \frac{1}{e}$

D. $I = 1$

Xem đáp án

Câu 38:

21/07/2024

Một vật đang chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc $a (t) = t^{2} + 3 t (m / s^{2})$ . Tính quãng đường mà vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.

A. $\frac{4300}{3} (m)$

B. $\frac{430}{3} (m)$

C. $\frac{3400}{3} (m)$

D. $\frac{340}{3} (m)$

Xem đáp án

Câu 39:

21/07/2024

Cho hình chóp SABC có đáy là tam giác vuông cân tại A, BC=2a, góc giữa các cạnh bên và mặt đáy bằng $60 °$ . Hỏi thể tích của khối chóp SABC bằng bao nhiêu?

A. $a^{3} \sqrt{2}$

B. $a^{3} \frac{\sqrt{3}}{3}$

C. $2 a^{3} \sqrt{2}$

C. $3 a^{3} \sqrt{3}$

Xem đáp án

Câu 40:

22/07/2024

Cho lăng trụ đứng ABCA'B'C'có đáy là tam giác vuông tạiA, AC=a, $\hat{A C B} = 60 °$ , góc giữa BC' và mặt phẳng (AA'C'C) bằng $30 °$ . Tính thể tích của khối lăng trụ ABCA'B'C'

A. $a^{3} \sqrt{6}$

B. $\frac{a^{3} \sqrt{6}}{3}$

C. $\frac{2 a^{3} \sqrt{6}}{3}$

D. $\frac{4 a^{3} \sqrt{6}}{3}$

Xem đáp án

Câu 41:

21/07/2024

Viết phương trình mặt phẳng (P) song song với (Q): x+2y-2z-1=0 sao cho điểm A(-1; 2; -1) cách đều (P) và (Q)

A. x+2y+2z+3=0

B. x+2y-2z-3=0

C. x+2y-2z-9=0

D. x+2y+2z+5=0

Xem đáp án

Câu 42:

22/07/2024

Cho 2 đường thẳng $d_{1} \{\begin{array}{l} \begin{array}{l} x = 4 + 2 t \\ y = 4 + 2 t \end{array} \\ z = - 3 - t \end{array}, d_{2} : \frac{x - 1}{3} = \frac{y + 1}{2} = \frac{z - 2}{- 2}$ Viết phương trình đường thẳng $∆$ cắt và vuông góc với cả 2 đường thẳng trên

A. $∆ : \frac{x - 1}{2} = \frac{y + 1}{2} = \frac{z - 2}{- 1}$

B. $∆ : \frac{x - 4}{3} = \frac{y - 4}{2} = \frac{z + 3}{- 2}$

C. $∆ : \frac{x - 5}{- 2} = \frac{y - 3}{1} = \frac{z + 1}{- 2}$

D. $∆ : \frac{x - 4}{2} = \frac{y - 1}{- 1} = \frac{z}{2}$

Xem đáp án

Câu 43:

22/07/2024

Một cái hộp không nắp được làm từ một miếng bìa các tông theo mẫu ở hình vẽ bên. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích của hộp là $500 c m^{3}$ . Tìm x để nguyên liệu làm hộp tốn ít nhất.

A. x=8

B. x=5

C. x=10

D. x=12

Xem đáp án

Câu 44:

21/07/2024

Tìm các giá trị của m để hàm số $y = \frac{2^{- x} - 2}{2^{- x} - m}$ nghịch biến trên khoảng (-1; 1)

A. $m \leq \frac{1}{2}, m > 2$

B. $m \leq \frac{1}{2}$

C. $m > 2$

D. $m \leq 2$

Xem đáp án

Câu 45:

21/07/2024

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị (C) như hình vẽ bên. Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành

A. $\frac{14}{3}$

B. $\frac{27}{4}$

C. $\frac{31}{5}$

D. $\frac{5}{31}$

Xem đáp án

Câu 46:

21/07/2024

Cho số phức $z = 1 + (1 + i) + {(1 + i)}^{2} + . . . + {(1 + i)}^{2012}$ . Mệnh đề nào dưới đây đúng

A. $z c ó p h ầ n t h ự c b ằ n g - 2^{1006}, p h ầ n ả o b ằ n g 1 + 2^{1006}$

B. $z c ó p h ầ n t h ự c b ằ n g 2^{1006}, p h ầ n ả o b ằ n g 1 - 2^{1006}$

C. $z c ó p h ầ n t h ự c b ằ n g - 2^{1008}, p h ầ n ả o b ằ n g 1 + 2^{1008}$

D. $z c ó p h ầ n t h ự c b ằ n g 2^{1008}, p h ầ n ả o b ằ n g 1 - 2^{1008}$

Xem đáp án

Câu 47:

21/07/2024

Cho hình chóp SABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác đều cạnh a, mp (SAB) vuông góc với đáy, thể tích của khối chóp bằng $a^{3}$ . Tính khoảng cách giữa hai đường thẳng SA và CD

A. $a \sqrt{3}$

B. $2 a \sqrt{3}$

C. $\frac{2 a}{\sqrt{3}}$

D. $\frac{a}{2}$

Xem đáp án

Câu 48:

21/07/2024

Xét một mô hình như sau. Từ hình vuông ABCD tâm I và có cạnh bằng 8, người ta cắt bỏ đi hai tam giác IAD, IBC, sau đó dán lên phần còn lại một hình vuông khác sao cho các đỉnh của hình vuông này trùng với các trung điểm của IA, IB, IC, ID như hình vẽ bên. Quay mô hình này xung quanh đường thẳng đi qua I và trung điểm của AB. Tính thể tích của vật thể tròn xoay thu được

A. $\frac{160 π}{3}$

B. $\frac{227 π}{3}$

C. $\frac{172 π}{3}$

D. $\frac{127 π}{3}$

Xem đáp án

Câu 49:

21/07/2024

Cho 3 điểm A(1; -1; -1), B(-1; 1; -1), C(-1; 0; 0). Viết phương trình mặt cầu (S), biết (S) nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn.

A. $(S) : x^{2} + y^{2} + {(z + 1)}^{2} = 2$

B. $(S) : x^{2} + y^{2} + {(z - 1)}^{2} = 2$

C. $(S) : x^{2} + y^{2} + {(z + 1)}^{2} = 4$

D. $(S) : x^{2} + y^{2} + {(z - 1)}^{2} = 4$

Xem đáp án

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3