Giải Toán 12 trang 62 Tập 1 Kết nối tri thức

Với giải bài tập Toán 12 trang 62 Tập 1 trong Bài 7: Hệ trục toạ độ trong không gian sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 12 trang 62 Tập 1.

1 135 09/06/2024

Trang trước

Trang sau

Giải Toán 12 trang 62 Tập 1

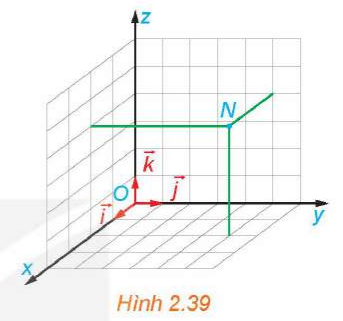
Luyện tập 2 trang 62 Toán 12 Tập 1: Tìm tọa độ của điểm N trong Hình 2.39.

Lời giải:

Ta có: $\vec{O N} = 2 \vec{i} + 5 \vec{j} + 4 \vec{k}$ . Do đó, N(2; 5; 4).

Luyện tập 3 trang 62 Toán 12 Tập 1: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’.

Lời giải:

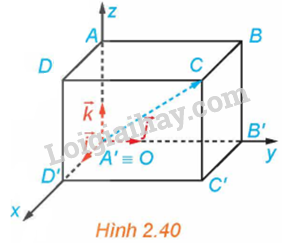
Tài liệu VietJack

Theo Ví dụ 3 ta có: $m = 2, n = 3, p = 5$ .

Vì ABB’O là hình bình hành nên $\vec{O B} = \vec{O B^{'}} + \vec{O A} = n \vec{j} + p \vec{k} = 3 \vec{j} + 5 \vec{k}$ . Do đó, B(0; 3; 5)

Vì OB’C’D’ là hình bình hành nên $\vec{O C^{'}} = \vec{O D^{'}} + \vec{O B^{'}} = m \vec{i} + n \vec{j} = 2 \vec{i} + 3 \vec{j}$ . Do đó, C’(2; 3; 0)

Vì ADD’A’ là hình bình hành nên $\vec{O D} = \vec{O A} + \vec{O D^{'}} = m \vec{i} + p \vec{k} = 2 \vec{i} + 5 \vec{k}$ . Do đó, D(2; 0; 5)

Vận dụng 1 trang 62 Toán 12 Tập 1: Trong tính huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn với hệ tọa độ đó.

Trong Hình 2.34, một chiếc bóng đèn cách sàn nhà là 2m, cách hai bức tường lần lượt là 1m và 1,5m.

Lời giải:

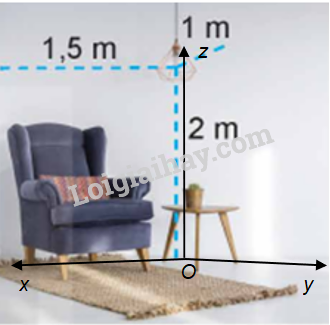
Tài liệu VietJack

Mô tả: Hệ tọa độ Oxyz có:

+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.

+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.

Khi đó, bóng đèn có tọa độ (1,5; 1; 2).

HĐ3 trang 62 Toán 12 Tập 1: Trong không gian Oxyz, cho vectơ $\vec{a}$ tùy ý (H.2.41). Lấy điểm M sao cho $\vec{O M} = \vec{a}$ và giải thích vì sao có bộ ba số (x; y; z) sao cho $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ .

Lời giải:

Theo khái niệm tọa độ trong không gian ta có: $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ . Mà $\vec{O M} = \vec{a}$ nên $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ . Do đó, có bộ ba số (x; y; z) sao cho $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ .

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

Giải Toán 12 trang 60 Tập 1

Giải Toán 12 trang 61 Tập 1

Giải Toán 12 trang 62 Tập 1

Giải Toán 12 trang 63 Tập 1

Giải Toán 12 trang 64 Tập 1

Giải Toán 12 trang 65 Tập 1

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 60 Toán 12 Tập 1: Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi $\vec{i}, \vec{j}, \vec{k}$ là các vectơ đơn vị trên các trục đó (H.2.35)...

Câu hỏi trang 61 Toán 12 Tập 1: Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không?...

Luyện tập 1 trang 61 Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng hướng...

HĐ2 trang 61 Toán 12 Tập 1: Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C...

Luyện tập 2 trang 62 Toán 12 Tập 1: Tìm tọa độ của điểm N trong Hình 2.39...

Luyện tập 3 trang 62 Toán 12 Tập 1: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’.

Vận dụng 1 trang 62 Toán 12 Tập 1: Trong tính huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn với hệ tọa độ đó...

HĐ3 trang 62 Toán 12 Tập 1: Trong không gian Oxyz, cho vectơ $\vec{a}$ tùy ý (H.2.41). Lấy điểm M sao cho $\vec{O M} = \vec{a}$ và giải thích vì sao có bộ ba số (x; y; z) sao cho $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ ...

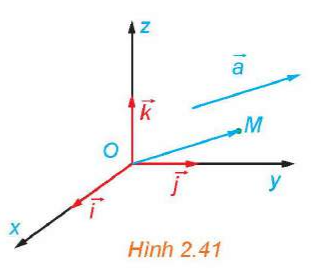
Luyện tập 4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, hãy xác định tọa độ của vectơ $\vec{i} + 2 \vec{j} + 5 \vec{k}$ .

HĐ4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, cho hai điểm $M (x; y; z)$ và $N (x^{'}; y^{'}; z^{'})$ .

a) Hãy biểu diễn hai vectơ $\vec{O M}$ và $\vec{O N}$ qua các vectơ $\vec{i}, \vec{j}$ và $\vec{k}$ ...

Luyện tập 5 trang 64 Toán 12 Tập 1: Trong Ví dụ 5, xác định tọa độ của các điểm D và D’ sao cho ABCD.A’B’C’D’ là hình hộp.

Vận dụng 2 trang 64 Toán 12 Tập 1: Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ tọa độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu,...

Bài 2.13 trang 64 Toán 12 Tập 1: Trong không gian Oxyz, cho ba vectơ $\vec{a}$ , $\vec{b}$ , $\vec{c}$ đều khác $\vec{0}$ và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?...

Bài 2.14 trang 64 Toán 12 Tập 1: Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy)...

Bài 2.15 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của vectơ $\vec{A B}$ trong mỗi trường hợp sau: a) $A (0; 0; 0)$ và $B (4; 2; - 5)$ ; b) $A (1; - 3; 7)$ và $B (1; - 3; 7)$ ;...

Bài 2.16 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau: a) A trùng với gốc tọa độ; b) A nằm trên tia Ox và $O A = 2$ ;...

Bài 2.17 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ...

Bài 2.18 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có

A (1; 1; - 1), B (0; 3; 0), C^{'} (2; - 3; 6)

. a) Xác định tọa độ của điểm C...

Bài 2.19 trang 65 Toán 12 Tập 1: Trong vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0)...

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài 6: Vectơ trong không gian

Bài 8: Tính đơn điệu và cực trị của hàm số

Bài tập cuối chương 2 trang 73, 74

Bài 9: Khoảng biến thiên và khoảng tứ phân vị

Bài 10: Phương sai và độ lệch chuẩn

1 135 09/06/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: