Nội dung bài viết

    Xem thêm

    Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME

    Lời giải HĐ2 trang 61 Toán 12 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 204 09/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Kết nối tri thức Bài 7: Hệ trục toạ độ trong không gian

    HĐ2 trang 61 Toán 12 Tập 1: Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C lần lượt thuộc các tia Ox, Oy, Oz (H.2.37).

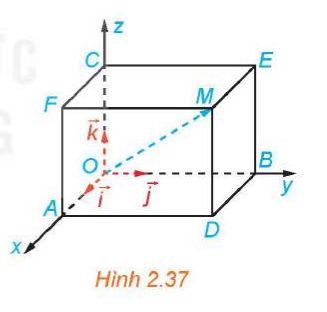
    Tài liệu VietJack

    a) Hai vectơ OM→ và OA→+OB→+OC→ có bằng nhau hay không?

    b) Giải thích vì sao có thể viết OM→=xi→+yj→+zk→ với x, y, z là các số thực.

    Lời giải:

    a) Vì OADB.CFME là hình hộp chữ nhật nên theo quy tắc hình hộp ta có: OM→=OA→+OB→+OC→

    b) Vì i→ là vectơ đơn vị trên trục Ox nên OA→=xi→ với x là số thực.

    Vì j→ là vectơ đơn vị trên trục Oy nên OB→=yj→ với y là số thực.

    Vì k→ là vectơ đơn vị trên trục Oz nên OC→=zk→ với z là số thực.

    Do đó, OM→=OA→+OB→+OC→=xi→+yj→+zk→ với x, y, z là các số thực.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    HĐ1 trang 60 Toán 12 Tập 1: Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi i→,j→,k→ là các vectơ đơn vị trên các trục đó (H.2.35)...

    Câu hỏi trang 61 Toán 12 Tập 1: Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không?...

    Luyện tập 1 trang 61 Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ i→,j→,k→ lần lượt cùng hướng...

    HĐ2 trang 61 Toán 12 Tập 1: Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C...

    Luyện tập 2 trang 62 Toán 12 Tập 1: Tìm tọa độ của điểm N trong Hình 2.39...

    Luyện tập 3 trang 62 Toán 12 Tập 1: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’.

    Vận dụng 1 trang 62 Toán 12 Tập 1: Trong tính huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn với hệ tọa độ đó...

    HĐ3 trang 62 Toán 12 Tập 1: Trong không gian Oxyz, cho vectơ a→ tùy ý (H.2.41). Lấy điểm M sao cho OM→=a→ và giải thích vì sao có bộ ba số (x; y; z) sao cho a→=xi→+yj→+zk→...

    Luyện tập 4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, hãy xác định tọa độ của vectơ i→+2j→+5k→.

    HĐ4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, cho hai điểm M(x;y;z) và N(x′;y′;z′).

    a) Hãy biểu diễn hai vectơ OM→ và ON→ qua các vectơ i→,j→ và k→...

    Luyện tập 5 trang 64 Toán 12 Tập 1: Trong Ví dụ 5, xác định tọa độ của các điểm D và D’ sao cho ABCD.A’B’C’D’ là hình hộp.

    Vận dụng 2 trang 64 Toán 12 Tập 1: Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ tọa độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu,...

    Bài 2.13 trang 64 Toán 12 Tập 1: Trong không gian Oxyz, cho ba vectơ a→, b→, c→ đều khác 0→ và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?...

    Bài 2.14 trang 64 Toán 12 Tập 1: Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy)...

    Bài 2.15 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của vectơ AB→ trong mỗi trường hợp sau: a) A(0;0;0) và B(4;2;−5); b) A(1;−3;7) và B(1;−3;7);...

    Bài 2.16 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau: a) A trùng với gốc tọa độ; b) A nằm trên tia Ox và OA=2;...

    Bài 2.17 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ...

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 6: Vectơ trong không gian

    Bài 8: Tính đơn điệu và cực trị của hàm số

    Bài tập cuối chương 2 trang 73, 74

    Bài 9: Khoảng biến thiên và khoảng tứ phân vị

    Bài 10: Phương sai và độ lệch chuẩn

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 204 09/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: