Đề thi Toán lớp 10 Giữa học kì 1 năm 2021 - 2022 có đáp án (4 đề)
4 Đề thi Học kì 1 Toán lớp 10 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 10 Học kì 1. Mời các bạn cùng đón xem:
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
A. PHẦN TRẮC NGHIỆM (8 điểm)
Câu 1: Trong mặt phẳng tọa độ Oxy, cho các vecto →u=(2;−4);→a=(−1;−2);→b=(1;−3) . Biết →u=m→a+n→b, tính m−n .
A. 5
B. -2
C. -5
D. 2
Lời giải
→u=m→a+n→b⇔{2=−m+n−4=−2m−3n⇔{m=−25n=85⇒m−n=−2
Chọn B.
Câu 2: Tìm m để hàm số y=(−2m+1)x+m−3 đồng biến trên ℝ ?
A. m<12
B. m>12
C. m<3
D. m>3
Lời giải
Hàm số đồng biến trên R⇔−2m+1>0⇔m<12 .
Chọn A.
Câu 3: Cho cotα=−√2(0°. Tính và .
A.
B.
C.
D.
Lời giải
Ta có:
Do
Chọn B.
Câu 4: Xác định phần bù của tập hợp trong .
A.
B.
C.
D.
Lời giải

Chọn C.
Câu 5: Xác định số phần tử của tập hợp .
A. 505
B. 503
C. 504
D. 502
Lời giải
Viết tập hợp X dưới dạng liệt kê và sử dung công thức:
Số số hạng = (Số cuối - Số đầu): Khoảng cách + 1
Tập hợp trên có .
Chọn A.
Câu 6: Cho phương trình . Có bao nhiêu giá trị của tham số m để phương trình có tập nghiệm là R?
A. vô số
B. 2
C. 1
D. 0
Lời giải
Phương trình ax + b = 0 có tập nghiệm
Phương trình có tập nghiệm là R .
Vậy m = 2.
Chọn C.
Câu 7: Khoảng đồng biến của hàm số là:
A.
B.
C.
D.
Lời giải
Ta có:
Vậy hàm số đồng biến trên .
Chọn B.
Câu 8: Xác định phần bù của tập hợp trong tập R?
A.
B.
C.
D.
Lời giải

Vậy
Chọn D.
Câu 9: Cho . Tính .
A.
B.
C.
D.
Lời giải
Chọn D.
Câu 10: Cho tam giác ABC vuông tại A có . Tính theo a?
A.
B.
C.
D.
Lời giải
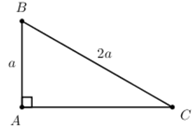
Ta có
Áp dụng định lý Pytago ta có:
Chọn D.
Câu 11: Khẳng định nào sau đây là khẳng định đúng?
A.
B.
C.
D.
Lời giải
Sử dụng tính chất “cos đối, sin bù, phụ chéo, hơn kém nhau π thì tan và cot”.
Khẳng định đúng là:
Chọn A.
Câu 12: Điểm A có hoành độ và thuộc đồ thị hàm số . Tìm m để điểm A nằm trong nửa mặt phẳng tọa độ phía trên trục hoành (không chứa trục hoành).
A.
B.
C.
D.
Lời giải
Do điểm A thuộc đồ thị hàm số .
Điểm A nằm trong nửa mặt phẳng tọa độ phía trên trục hoành (không chứa trục hoành)
Chọn D
Câu 13: Cho hình thang ABCD có . Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài của vectơ .
A.
B.
C.
D.
Lời giải
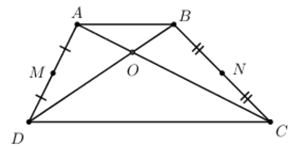
(Do MN là đường trung bình của hình thang ABCD).
Chọn C.
Câu 14: Tìm tập xác định của phương trình ?
A.
B.
C.
D.
Lời giải
Hàm số xác định
Chọn C.
Câu 15: Viết phương trình trục đối xứng của đồ thị hàm số ?
A.
B.
C.
D.
Lời giải
Trục đối xứng của đồ thị hàm số là .
Chọn A.
Câu 16: Cho tam giác ABC có G là trọng tâm, I là trung điểm của BC. Tìm khẳng định sai?
A.
B.
C.
D.
Lời giải
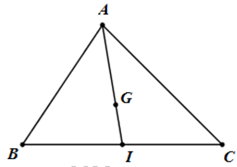
Do I là trung điểm của đúng.
sai.
Chọn B.
Câu 17: Cho hai tập hợp X, Y thỏa mãn và . Xác định số phần tử là số nguyên của X.
A. 2
B. 5
C. 3
D. 4
Lời giải
Số phần tử nguyên của X là .
Chọn D.
Câu 18: Tìm m để parabol cắt trục hoành tại 2 điểm phân biệt có hoành độ sao cho .
A.
B. Không tồn tại m
C.
D.
Lời giải
Xét phương trình hoành độ giao điểm: .
Để cắt trục hoành tại 2 điểm phân biệt có hoành độ thì phương trình (*) có 2 nghiệm phân biệt.
Ta có
Khi đó theo hệ thức Vi-ét ta có:
Theo đề bài ta có
Chọn A.
Câu 19: Có nhiều nhất bao nhiêu số nguyên m thuộc nửa khoảng để phương trình có nghiệm?
A. 2014
B. 2021
C. 2013
D. 2020
Lời giải
Để phương trình ban đầu có nghiệm phương trình có nghiệm .
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
Xét hàm số ta có BBT:
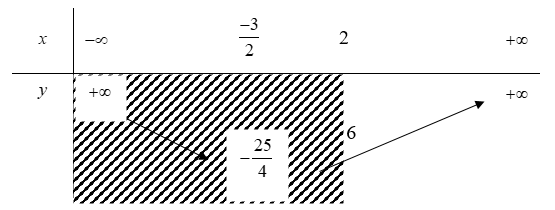
Dựa vào BBT ta có để phương trình có nghiệm khi và chỉ khi .
Kết hợp điều kiện đề bài ta có , có số nguyên m thỏa mãn.
Chọn A.
Câu 20: Trong mặt phẳng Oxy, cho các điểm . Tính độ dài AB?
A.
B.
C.
D.
Lời giải
Chọn A.
Câu 21: Tập hợp nào sau đây chỉ gồm các số vô tỷ?
A.
B.
C.
D.
Lời giải
Tập hợp chỉ gồm các số vô tỉ là .
Chọn B.
Câu 22: Tìm m để phương trình có 2 nghiệm phân biệt?
A. và
B. và
C. và
D.
Lời giải
ĐK:
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm phân biệt khác -1.
Vậy và
Chọn B.
Câu 23: Cho hàm số . Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng .
A.
B.
C.
D.
Lời giải
Thay ta có:
Suy ra điểm cần tìm có tọa độ .
Chọn B.
Câu 24: Cho phương trình (m là tham số). Khẳng định nào sau đây đúng?
A. thì phương trình có tập nghiệm
B. và thì phương trình có tập nghiệm .
C. thì phương trình có tập nghiệm R.
D. và thì phương trình vô nghiệm.
Lời giải
Khi đó, phương trình có nghiệm duy nhất .
Chọn B.
Câu 25: Cho hình bình hành ABCD có N là trung điểm của AB và G là trọng tâm tam giác ABC. Phân tích theo và ?
A.
B.
C.
D.
Lời giải
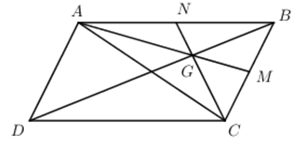
Gọi M là trung điểm của BC ta có:
Chọn D.
Câu 26: Cho hình bình hành ABCD có N là trung điểm của AB, BC, CA. Khi đó vectơ là vectơ nào sau đây?
A.
B.
C.
D.
Lời giải
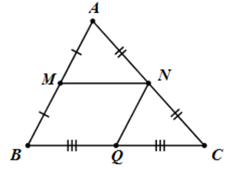
Ta có MN là đường trung bình của tam giác ABC
Chọn A.
Câu 27: Tìm phương trình tương đương với phương trình trong các phương trình sau:
A.
B.
C.
D.
Lời giải
, ĐK:
Kết hợp điều kiện, suy ra tập nghiệm của phương trình là
Chọn A.
Câu 28: Giải phương trình
A.
B.
C.
D.
Lời giải
Vậy tập nghiệm của phương trình là
Chọn D.
Câu 29: Cho tam giác ABC và điểm I thỏa mãn . Phân tích theo và .
A.
B.
C.
D.
Lời giải
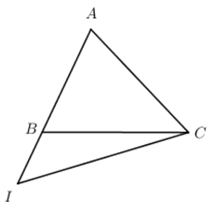
Ta có:
(1)
(2)
Cộng vế theo vế của (1) với (2) ta được:
Do
Chọn C.
Câu 30: Cho tam giác ABC có . Tìm tọa độ trực tâm H của tam giác ABC.
A.
B.
C.
D.
Lời giải
Gọi . Ta có:
H là trực tâm của tam giác ABC
Chọn C.
Câu 31: Đồ thị bên là của hàm số nào sau đây?
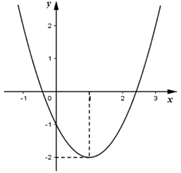
A.
B.
C.
D.
Lời giải
Trong 4 đáp án chỉ có parabol có đỉnh .
Chọn D.
Câu 32: Tìm tập xác định của hàm số .
A.
B.
C.
D.
Lời giải
Hàm số xác định Chọn D.
Câu 33: Trên mặt phẳng tọa độ Oxy, cho vuông tại A có và . Tìm tọa độ điểm H là chân đường cao kẻ từ đỉnh A của tam giác ABC, biết .
A.
B.
C.
D.
Lời giải
Phương trình .
Vì .
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có
Ta lại có
Chọn B.
Câu 34: Cho hai tập hợp , tập hợp có bao nhiêu phần tử?
A. 9
B. 7
C. 8
D. 10
Lời giải
Chọn C.
Câu 35: Trong mặt phẳng tọa độ Oxy, cho các vectơ và . Tìm m để hai vectơ cùng phương?
A.
B.
C.
D.
Lời giải
Hai vectơ cùng phương sao cho .
Chọn D.
Câu 36: Tìm m để hàm số có giá trị nhỏ nhất trên bằng .
A.
B.
C.
D.
Lời giải
Ta có Hàm số đồng biến trên Hàm số đồng biến trên
Chọn A.
Câu 37: Cho hình vuông ABCD có cạnh bằng 1. Hai điểm M, N thay đổi lần lượt trên AB, D sao cho và . Tìm mối liên hệ giữa x và y sao cho .
A.
B.
C.
D.
Lời giải
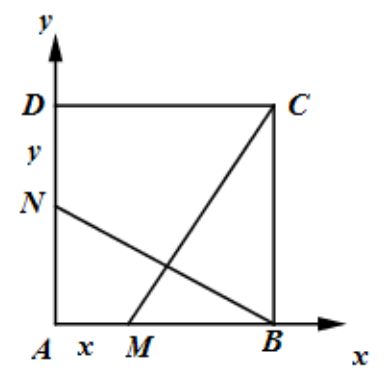
Gắn hệ trục tọa độ như hình vẽ ta có
Chọn A.
Câu 38: Xác định các hệ số a và b để Parabol có đỉnh .
A.
B.
C.
D.
Lời giải
Ta có:
Chọn C.
Câu 39: Cho P là mệnh đề đúng, Q là mệnh đề sai, chọn mệnh đề đúng trong các mệnh đề sau:
A.
B.
C.
D.
Lời giải
P đúng sai sai.
P đúng, Q sai sai sai.
P đúng, Q sai sai đúng.
Q sai đúng, P đúng sai sai.
Chọn C.
Câu 40: Tìm m để Parabol có trục đối xứng đi qua điểm ?
A.
B.
C.
D.
Lời giải
Trục đối xứng của là (d)
Chọn D.
II. PHẦN TỰ LUẬN (2 điểm)
Câu 1: Giải phương trình (1)
Lời giải
ĐK:
Vậy x = 0 là nghiệm của phương trình.
Câu 2: Trên mặt phẳng tọa độ Oxy, cho và . Đặt . Gọi là vectơ ngược chiều với . Tìm x biết .
Lời giải
Khi (tm)
Khi (ktm)
Vậy .
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
Câu 1: Tập hợp nào sau đây có đúng hai tập hợp con?
A.
B.
C.
D.
Phương pháp:
Tập hợp có đúng hai tập con là tập hợp có đúng 1 phần tử.
Cách giải:
Tập hợp có các tập con là
Tập hợp có các tập con là:
Tập hợp có các tập con là
Tập hợp có các tập con là
Chọn B.
Câu 2: Cho . Khi đó là:
A.
B.
C.
D.
Lời giải
Phương pháp:
Cách giải:
Ta có:
![]()
![]()
Chọn A.
Câu 3: Parabol có hoành độ đỉnh là:
A.
B.
C.
D.
Lời giải
Phương pháp:
Hoành độ đỉnh của parabol là .
Cách giải:
Hoành độ đỉnh của là: .
Chọn C.
Câu 4: Số nghiệm của phương trình là:
A. 2
B. 0
C. 1
D. 3
Lời giải
Phương pháp:
+) Tìm ĐKXĐ.
+) Quy đồng bỏ mẫu và giải phương trình.
Cách giải:
ĐKXĐ:
Kết hợp với điều kiện, suy ra phương trình đã cho vô nghiệm.
Chọn B.
Câu 5: Phương trình có bao nhiêu nghiệm?
A. Vô số
B. 1
C. 0
D. 2
Lời giải
Phương pháp:
Cách giải:
ĐK:
PT
Vậy phương trình đã cho vô nghiệm
Chọn C.
Câu 6: Chiều cao của một ngọn đồi là . Độ chính xác d của phép đo trn là:
A.
B.
C.
D.
Lời giải
Độ chính xác d của phép đo trên là
Chọn B.
Câu 7: Trong mặt phẳng tọa độ Oxy cho hai điểm . Trung điểm I của đoạn thẳng AB có tọa độ là:
A.
B.
C.
D.
Lời giải
Phương pháp:
Tọa độ trung điểm I của AB là:
Cách giải:
Chọn D.
Câu 8: Theo thống kê, dân số Việt Nam năm 2016 được ghi lại như sau (người). Số quy tròn của số gần đúng là 94444200 là:
A.
B.
C.
D. 94400000
Lời giải
Chữ số hàng nghìn quy tròn
Chọn A.
Câu 9: Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng để đường thẳng cắt Parabol tại hai điểm phân biệt nằm về cùng một phía đối với trục tung?
A. 6
B. 5
C. 7
D. 8
Lời giải
Phương pháp:
Để đường thẳng (d) cắt (P) tại hai điểm phân biệt nằm về cùng phía đối với trục tung thì phương trình hoành độ giao điểm có 2 nghiệm phân biệt cùng dấu.
Cách giải:
Xét phương trình hoành độ giao điểm
Để đường thẳng (d) cắt (P) tại hai điểm phân biệt về cùng phía đối với trục tung thì phương trình (*) có 2 nghiệm phân biệt cùng dấu.
Kết hợp điều kiện đề bài ta có
Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A.
Câu 10: Cho với 4 điểm A, B, C, D bất kì. Chọn khẳng định đúng?
A.
B.
C.
D.
Lời giải
Chọn C.
Câu 11: Cho các câu sau đây:
(I): “Phan-xi-păng là ngọn núi cao nhất Việt Nam”.
(II): “ ”
(III): “Mệt quá!”
(IV): “Chị ơi, mấy giờ rồi?”
Hỏi có bao nhiêu câu là mệnh đề?
A. 1
B. 3
C. 4
D. 2
Lời giải
Có 2 mệnh đề là (I) và (II).
Chọn D.
Câu 12: Hàm số nào sau đây là hàm số lẻ?
A.
B.
C.
D.
Lời giải
Phương pháp:
Cho hàm số có TXĐ D.
Hàm số được gọi là hàm số chẵn nếu
Hàm số được gọi là hàm số lẻ nếu
Cách giải:
Xét hàm số có TXĐ:
Ta có: là hàm số lẻ.
Chọn C.
Câu 13: Một giá đỡ được gắn vào bức tường như hình vẽ. Tam giác ABC vuông cân ở đỉnh C. Người ta treo vào điểm A một vật có trọng lượng 10N. Khi đó lực tác động vào bức tường tại hai điểm B và C có cường độ lần lượt là: 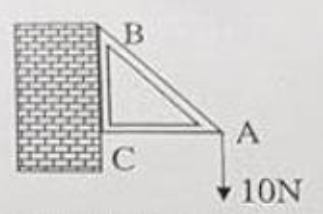
A. và 10N
B. 10N và 10N
C. 10N và
D. và
Lời giải
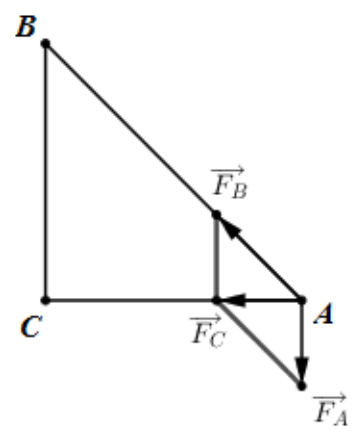
Áp dụng quy tắc tổng hợp lực ta có:
Vì tam giác ABC cân tại C
Áp dụng định lí Pytago ta có:
Chọn A.
Câu 14: Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có . Tọa độ đỉnh D là:
A.
B.
C.
D.
Lời giải
Ta có:
Để ABCD là hình bình hành .
Chọn A.
Câu 15: Cho hàm số có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
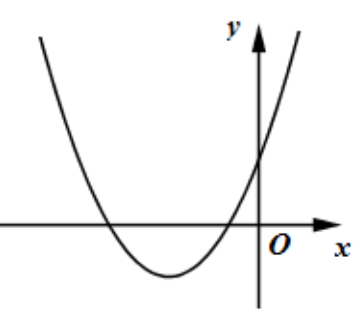
A.
B.
C.
D.
Lời giải
Phương pháp:
+) Dựa vào hướng bề lõm của parabol xác định dấu của a.
+) Dựa vào giao điểm của parabol với trục tung xác định dấu của c.
+) Dựa vào hoành độ đỉnh xác đinh dấu của b.
Cách giải:
Parabol có bề lõm hướng lên trên
Đồ thị hàm số cắt trục tung tại điểm
Hoành độ đỉnh của parabol là , mà .
Chọn B.
Câu 16: Gọi n là số các giá trị của tham số m để phương trình có nghiệm duy nhất. Khi đó n là:
A. 2
B. 1
C. 0
D. 3
Lởi giải
ĐK:
Giải (*)
TH1: (Vô nghiệm) Phương trình ban đầu có nghiệm duy nhất .
thỏa mãn
TH2:
Để phương trình ban đầu có nghiệm duy nhất
Vậy . Khi đó .
Chọn D.
Câu 17: Cho hình vuông ABCD cạnh a. Tính ?
A. 3a
B.
C.
D.
Lời giải
Theo quy tắc hình bình hành:
Áp dụng định lí pytago vào tam giác ABC có:
Chọn D.
Câu 18: Cho mệnh đề: “Có một học sinh lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. “Mọi học sinh lớp 10A đều thích học môn Toán”.
B. “Mọi học sinh lớp 10A đều không thích học môn Toán.”
C. “Mọi học sinh lớp 10A đều thích học môn Văn”.
D. “Có một học sinh lớp 10A thích học môn Toán”.
Lời giải
“Có một học sinh lớp 10A không thích học môn Toán”.
Mệnh đề phủ định của mệnh đề này là: “Mọi học sinh lớp 10A đều thích học môn Toán”.
Chọn A.
Câu 19: Cho . Khẳng định nào dưới đây đúng?
A.
B.
C.
D.
Lời giải
Sử dụng tính chất “cos đối, sin bù, phụ chéo, hơn kém nhau thì tan và cot”.
Ta có:
Chọn B.
Câu 20: Phương trình có hai nghiệm phân biệt khi:
A.
B.
C.
D.
Lời giải
Phương trình có 2 nghiệm phân biệt
Chọn A.
Câu 21: Biết . Hỏi giá trị của là bao nhiêu?
A.
B.
C.
D.
Lời giải
Ta có:
Vì nên
Chọn B.
Câu 22: Trong mặt phẳng tọa độ Oxy, cho . Điểm M thỏa mãn . Tọa độ điểm M là:
A.
B.
C.
D.
Lời giải
Gọi ta có:
Chọn A.
Câu 23: Đường thẳng đi qua điểm và vuông góc với đường thẳng có phương trình là:
A.
B.
C.
D.
Lời giải
Gọi d’ là đường thẳng đi qua M và vuông góc với d, do đó phương trình d’ có dạng: .
.
Vậy .
Chọn A.
Câu 24: Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình có tập nghiệm là . Tính tổng tất cả các phần tử của S.
A. 1
B.
C. 2
D. 0
Lời giải
Phương pháp:
Phương trình bậc nhất .
+) : phương trình có vô số nghiệm
+) : phương trình vô nghiệm
+) : phương trình có nghiệm duy nhất .
Cách giải:
Để phương trình trên có tập nghiệm
Chọn A.
Câu 25: Hàm số nào sau đây có tập xác định ?
A.
B.
C.
D.
Lời giải
Hàm số xác định .
Hàm số xác định .
Hàm số xác định (luôn đúng)
Hàm số xác định .
Chọn C.
PHẦN TỰ LUẬN (5,0 điểm )
Câu 1 (2 điểm): Cho hàm số (1)
a) (1 điểm) Lập bảng biến thiên và vẽ đồ thị của hàm số (1).
b) (1 điểm) Viết phương trình đường thẳng đi qua giao điểm của với trục Oy và song song với đường thẳng
Lởi giải
a) Lập bảng biến thiên và vẽ đồ thị của hàm số (1).
TXĐ:
Tọa độ đỉnh , trục đối xứng
Hàm số nghịch biến trên và đồng biến trên
Bảng biến thiên:
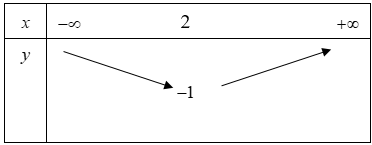
*) Đồ thị hàm số:
Giao với trục Ox: Cho
Giao với trục Oy: Cho .
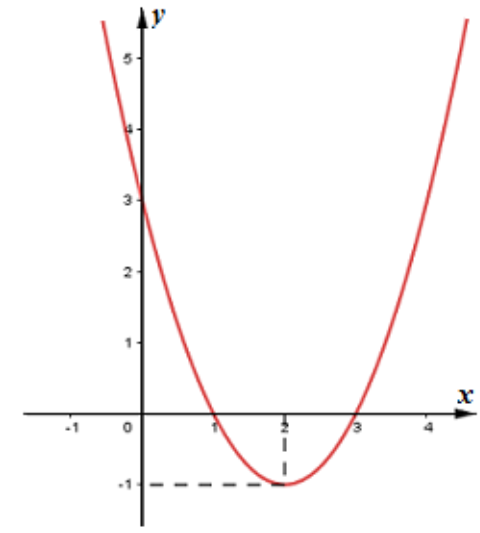
b)
Gọi d là đường thẳng đi qua A và song song với đường thẳng , khi đó phương trình (d) có dạng .
Câu 2: Tìm m để phương trình có 2 nghiệm thỏa mãn .
Lời giải
Ta có:
Để phương trình có 2 nghiệm .
Theo hệ thức Vi-ét ta có:
Để 2 nghiệm thỏa mãn ta có:
Giải (*):
Vậy .
Câu 3: (2 điểm) Cho tam giác ABC. Trên cạnh AC lấy điểm D, trên cạnh BC lấy điểm E sao cho , .
a) (1 điểm) Biểu diễn mỗi vectơ theo hai vectơ .
b) (0,5 điểm) Tìm tập hợp điểm M sao cho
c) (0,5 điểm) Với k là số thực tùy ý, lấy các điểm P, Q sao cho . Chứng minh rằng trung điểm của đường thẳng PQ luôn thuộc một đường thẳng cố định khi k thay đổi.
Lời giải
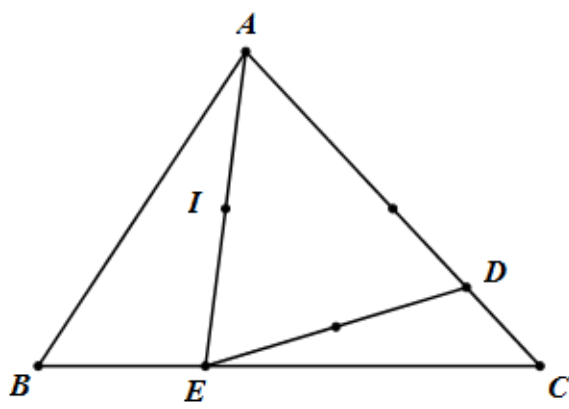
a) Ta có:
b) Gọi I là trung điểm của AE ta có:
Do B, D cố định không đổi không đổi.
A, E cố định I cố định.
Do đó tập hợp điểm M là đường tròn tâm I bán kính .
c) Khi
Trung điểm của PQ trùng với trung điểm của DE.
Khi
Trung điểm của PQ trùng với trung điểm của AB.
Do AB, DE cố định Trung điểm của AB và DE cố định Đường thẳng đi qua trung điểm của AB và DE cố định.
Vậy khi k thay đổi thì trung điểm của PQ luôn thuộc đường thẳng cố định đi qua trung điểm của AB và DE.
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
