Đề thi học kì 2 Toán lớp 10 có đáp án (8 đề)
8 Đề thi Giữa học kì 2 Toán lớp 10 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 10 Giữa học kì 2. Mời các bạn cùng đón xem:
Đề thi học kì 2 Toán lớp 10 có đáp án (8 đề)
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
Đề thi học kì 2 Toán lớp 10 có đáp án đề số 1
A. PHẦN TRẮC NGHIỆM ( 3 điểm ) Chọn đáp án đúng trong mỗi câu sau:
Câu 1 (TH). Tập nghiệm của bất phương trình là:
A. (−∞;−3]∪[4;+∞).
B. ∅ .
C. (−∞;−4]∪[3;+∞) .
D. [−3;4] .
Lời giải
Vậy tập nghiệm của bất phương trình là [ -3; 4].
Chọn D
Câu 2 (TH). Tập nghiệm của bất phương trình x+12−x<0 là:
A. [−1;2] .
B. (−1;2)
C. (−∞;−1)∪(2;+∞) .
D. [−1;2) .
Lời giải
ĐKXĐ: 2−x≠0⇔x≠2
Đặt . Ta có bảng:
| x
|
−∞
|
-1 |
2 |
+∞
|
| x + 1
|
|
0 + |
|
+ |
| 2-x
|
+ |
+ |
0 |
- |
| f(x)
|
- |
0 + |
|
- |
Vậy f(x)<0⇔[x<−1x>2nen tập nghiệm của phương trình là (−∞;−1)∪(2;+∞)
Chọn C
Câu 3 (VD). Có bao nhiêu giá trị nguyên của tham số m để với mọi x∈R , biểu thức f(x)=x2+(m+2)x+8m+1 luôn nhận giá trị dương?
A. 27
B. 28
C. Vô số
D. 26
Lời giải
Ta có: f(x)=x2+(m+2)x+8m+1>0 với mọi x
⇔Δ=(m+2)2−4.(8m+1)<0⇔m2−28m<0⇔m(m−28)<0⇔0<m<28⇒m∈Z⇒m={1;2;3;...
Vậy có 27 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Chọn A
Câu 4 (NB). Cho bảng số liệu thống kê điểm kiểm tra 1 tiết môn Toán của 40 học sinh như sau:
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Số học sinh |
2 |
3 |
7 |
18 |
3 |
2 |
4 |
1 |
40 |
Số trung vị và mốt của bảng số liệu thống kê trên là:
A. = 8; = 40.
B. = 6; = 18.
C. =6,5; = 6.
D. =7; = 6.
Lời giải
Dựa vào bảng số liệu thống kê ta thấy
Chọn C.
Câu 5 (TH). Biểu thức có biểu thức rút gọn là:
A.
B.
C.
D.
Lời giải
Chọn B
Câu 6 (VD). Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ ( AB = 4,3cm; BC = 3,7cm; CA = 7,5cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy)
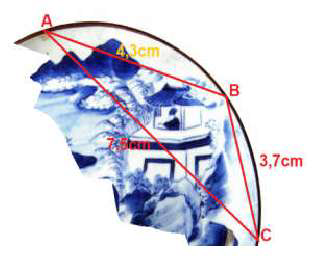
A. 5,73 cm
B. 6,01 cm
C. 5,85 cm
D. 4,57 cm
Lời giải
Dễ thấy bán kính của chiếc đĩa là bán kính đường tròn ngoại tiếp tam giác ABC
Tam giác ABC có nửa chu vi
Chọn A
Câu 7 (TH). Phương trình tham số của đường thẳng đi qua 2 điểm , là:
A.
B.
C.
D.
Lời giải
Đường thẳnng đi qua 2 điểm nên nhận làm VTCP
Phương trình tham số của đường thẳng AB là:
Chọn B.
Câu 8 (TH). Tìm tất cả các giá trị của tham số m để phương trình là phương trình đường tròn.
A. 1
B. m< - 2 hoặc m > - 1
C. m < - 2hoặc m > 1
D. m< 1 hoặc m> 2
Lời giải
Phương trình là phương trình đường tròn
Chọn D
II. PHẦN TỰ LUẬN (7 điểm)
Câu 1 (VD). Giải các bất phương trình sau
a)
b)
Lời giải
a)
ĐKXĐ:
Ta có:
Đặt . Ta có bảng:
| x
|
|
-1 |
1 |
4 |
|
|
+
|
0 |
|
0 |
|
|
|
|
0 + |
+ |
|
|
|
0 + |
|
0 + |
Vậy Tập nghiệm của phương trình là .
b)
Vậy tập nghiệm của bất phương trình là:
Câu 2 (VD) (1,5 điểm).
Cho góc α thỏa mãn và . Tính giá trị của biểu thức .
Lời giải
Vì thỏa mãn .
Câu 3 (VD) . Trong mặt phẳng với hệ tọa độ Oxy cho điểm A(3;1), đường thẳng và đường tròn :
a) Tìm tọa độ tâm, tính bán kính của đường tròn . Viết phương trình tiếp tuyến của đường tròn biết tiếp tuyến đó song song với đường thẳng .
b) Viết phương trình tổng quát của đường thẳng đi qua điểm A và cắt đường tròn tại hai điểm B, C sao cho .
c) Tìm tọa độ điểm nằm trên đường tròn sao cho biểu thức đạt giá trị lớn nhất, giá trị nhỏ nhất.
lời giải
a)
+) Đường tròn có tâm ,bán kính
+) Gọi là trình tiếp tuyến của đường tròn (C ) song song với đường thẳng
có phương trình dạng
Vì là trình tiếp tuyến của đường tròn (C) nên
.
Vậy có hai đường thẳng thỏa mãn đề bài là và
b)
Nhận thấy là đường kính .
Ta có:
Đường thẳng đi qua 2 điểm A và I nên nhận làm VTPT
Phương trình tổng quát của đường thẳng d là:
c)
Vì điểm nằm trên đường tròn nên ta có: (*)
. Thế vào (*) ta được:
(**)
Vì cần tồn tại điểm nên phương trình (**) phải có nghiệm
+) Với T = 1 (**)
+) Với T = 5 (**)
Vậy MinT = 1 khi M(0; 1), Max T = 5 khi M (2; 3).
Câu 4 (VDC) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [ 0; 2].
Lời giải
Ta có hàm số:
Đặt
Khi đó ta có hàm số:
Xét với
Ta có bảng:
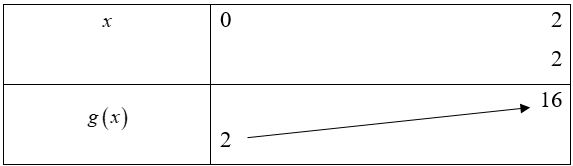
Với thì
Bài toán trở thành tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
Ta có bảng;
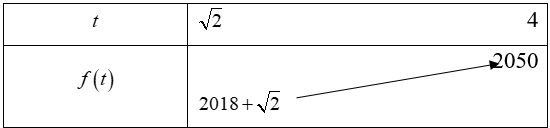
Vậy GTNN của hàm số bằng đạt được khi hay x = 0.
Vậy GTLN của hàm số bằng 2050 đạt được t = 4 hay x = 2 .
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
Đề thi học kì 2 Toán lớp 10 có đáp án đề số 2
A. PHẦN TRẮC NGHIỆM ( 5 điểm) Chọn đáp án đúng trong mỗi câu sau:
Câu 1 (NB). Cho tanx =2. Giá trị của biểu thức là
A. 2.
B. 13.
C. –9.
D. –2.
Lời giải
Ta có : thế vào P
Chọn B.
Câu 2 (VD). Bất phương trình có tập nghiệm là
A.
B. [3; 4].
C.
D.
Lời giải
ĐKXĐ:
Đặt . Ta có bảng:
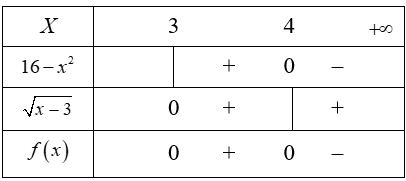
Vậy Tập nghiệm của phương trình là
Chọn D.
Câu 3 (NB). Trong mặt phẳng với hệ tọa độ Oxy, cho elíp ( E ) có phương trình chính tắc là . Tiêu cự của ( E) là.
A. 8.
B. 4.
C. 2.
D.16.
Lời giải
Ta có: Tiêu cự của là 2c = 2.4 = 8
Chọn A.
Câu 4 (TH). Cho hệ phương trình , với m là tham số. Tìm tất cả các giá trị của m để hệ trên có nghiệm.
A. .
B.
C.
D.
Lời giải
Phương pháp:
+) Biến đổi hệ phương trình sử dụng phương pháp rút thế.
+) Phương trình bậc 2 có nghiệm
Cách giải:
Để hệ phương trình có nghiệm có nghiệm
Chọn A.
Câu 5 (VD). Trong mặt phẳng với hệ tọa độ Oxy, cho A( -3 ; 5) ; B(1 ; 3) và đường thẳng d : 2x – y -1 = 0, đường thẳng AB cắt d tại I . Tính tỷ số
A. 6.
B. 2.
C. 4.
D. 1.
Lời giải
Ta có đường thẳng d có VTCP là
Đường thẳng (AB) vuông góc với đường thẳng (d)
Đường thẳng AB cắt d tại I nên IA; IB lần lượt là khoảng cách từ A và B đến đường thẳng d
Chọn A
Câu 6 (VD). Cho đường thẳng và đường tròn . Biết đường thẳng cắt ( C) tại hai điểm phân biệt A và B, khi đó độ dài đoạn thẳng AB là
A. 6.
B. 3.
C. 4.
D. 8.
Lời giải
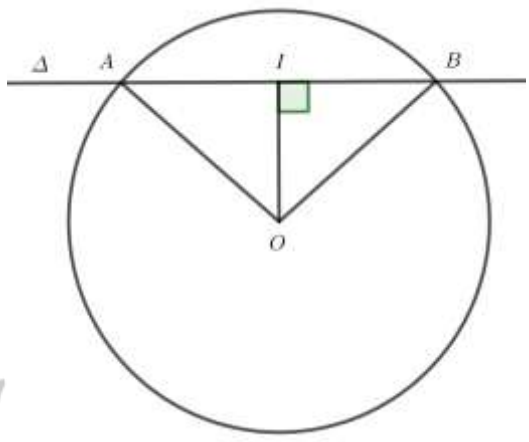
Đường tròn (C ) có:
tâm O(1; 1) bán kính R = OA = OB = 5
Gọi I là hình chiếu của O trên AB.
Chọn A.
Câu 7 (VDC). Cho a, b, c,d là các số thực thay đổi thỏa mãn
. Tìm giá trị lớn nhất của
A.
B.
C.
D.
Lời giải:
Ta có: Gọi a là góc có
Lại có: Gọi là góc có
Ta có:
Mà
Khi đó
Chọn B.
Câu 8 (NB). Cho đường thẳng d : 7x + 3y -1= 0. Vectơ nào sau đây là vectơ chỉ phương của d?
A. .
B.
C.
D.
Lời giải
Đường thẳng d có VTPT nên nhận là 1 VTCP
Chọn C.
Câu 9 (TH). Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Lời giải
ĐKXĐ:
Kết hợp ĐKXĐ nên tập nghiệm của bất phương trình là
Chọn D.
Câu 10 (TH). Cho . Tính .
A.
B.
C.
D.
Lời giải
Cách giải:
Ta có:
Do
Chọn C.
Câu 11. (TH). Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Lời giải
Tập nghiệm của bất phương trình là (-1 ; 2)
Chọn D.
Câu 12 (NB). Cho tam giác ABC, có độ dài ba cạnh là BC = a; AC = b; AB = c. Gọi là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh
đề nào sau đây sai?
A.
B.
C.
D.
Lời giải
Cho tam giác ABC, có độ dài ba cạnh là BC = a; AC = b; AB = c
Áp dụng hệ thức hàm số cos của tam giác ta có:
đáp B sai.
Chọn B.
Câu 13 (TH). Bất phương có tập nghiệm là
A.
B.
C.
D.
Lời giải
Tập nghiệm của bất phương trình là
Chọn C.
Câu 14.Tam thức không âm với mọi giá trị của x khi
A. m< 3
B.
C.
D.
Lời giải
Tam thức không âm với mọi giá trị của x
Chọn D.
Câu 15 (VD). Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Lời giải
Tập nghiệm của bất phương trình là
Chọn C.
Câu 16 (NB). Xác định tâm và bán kính của đường tròn
A. Tâm I(-1; 2), bán kính R = 3
B. Tâm I(-1; 2), bán kính R = 9
C. Tâm I(1; -2), bán kính R = 3
D. Tâm I(1; -2), bán kính R= 9
Lời giải
Đường tròn (C ) có tâm I (-1; 2), bán kính R = 3
Chọn A.
Câu 17 (VD). Tìm tất cả các giá trị của tham số m để bất phương trình
vô nghiệm.
A.
B.
C.
D.
Lời giải
Bất phương trình vô nghiệm
Chọn D.
Câu 18 (TH). Khẳng định nào sau đây Sai?
A.
C.
D.
Lời giải
Vì x = 4 là nghiệm BPT (2) nhưng không là nghiệm BPT (1) nên hai BPT trên không tương đương.
Chọn B.
Câu 19 (TH). Cho f(x); g(x) là các hàm số xác định trên , có bảng xét dấu như sau:
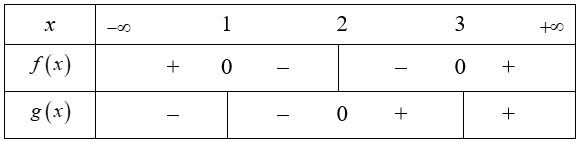
Khi đó tập nghiệm của bất phương trình là
A.
B.
C.
D. [1; 2]
Lời giải
Cho f(x); g(x) là các hàm số xác định trên R thì và
g (x) cùng dấu hoặc
Chọn B.
Câu 20 (VD). Cho a, b là các số thực dương, khi đó tập nghiệm của bất phương trình
là
A.
B.
C.
D.
Lời giải
Đặt . Ta có a, b là các số thực dương
Ta có bảng:
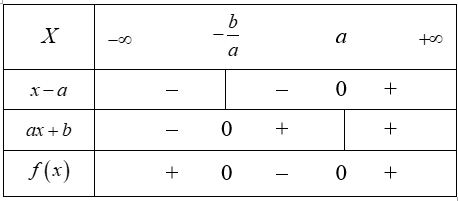
Vậy Tập nghiệm của phương trình là
Chọn C.
II. PHẦN TỰ LUẬN (5 điểm)
Câu I (VD) (3,0 điểm).
1) Giải phương trình
2) Giải hệ bất phương trình
Lời giải
Ta có
Vậy phương trình có nghiệm .
2) Giải hệ bất phương trình
Ta có
Vậy hệ bất phương trình có tập nghiệm là
Câu II (VD) (1,5 điểm). Trong mặt phẳng Oxy, cho đường tròn . Viết phương trình tiếp tuyến với đường tròn biết tiếp tuyến đó song song với đường thẳng
Lời giải
Đường tròn có tâm I(1; 4), bán kính R = 2.
Gọi d là tiếp tuyến cần tìm, do d song song với có dạng
d là tiếp tuyến với đường tròn
Với
Với
Vậy đường thẳng và đường thẳng thỏa mãn yêu cầu đề bài.
Câu III (VDC) (0,5 điểm). Cho hai số thực x, y thỏa mãn: . Tìm giá trị lớn nhất của biểu thức: P = x + y
Lời giải
Với ta có:
Dấu “=” của xảy ra khi a = b
Ta có:
Áp dụng (1) ta được:
Dấu “=” xảy ra
Vậy giá trị lớn nhất của biểu thức P bằng đạt tại
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
