Đề thi Giữa học kì 2 Toán lớp 10 Trắc nghiệm + Tự luận năm 2022 ( 4 đề)

Đề thi Giữa học kì 2 Toán lớp 10 Trắc nghiệm + Tự luận năm 2022 

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học 2021 - 2022

Môn: Toán 10

Thời gian làm bài: 45 phút

Đề thi Giữa học kì 2 Toán lớp 10 Trắc nghiệm + Tự luận năm 2022 đề số 1

Câu 1: Cho 2 đường thẳng  $\mathrm{\Delta }$ và $\mathrm{\Delta }\text{'}$ lần lượt có phương trình là $\sqrt{3}\mathrm{x}-\mathrm{y}+1-\sqrt{3}=0$  và $\mathrm{x}-\sqrt{3}\mathrm{y}-1+\sqrt{3}=0$. Góc giữa 2 đường thẳng $\mathrm{\Delta }$ và $\mathrm{\Delta }\text{'}$ là:

A. $60°$

B. $30°$

C. $0°$

D. $120°$

Câu 2:  Điều kiện xác định của hàm số $\mathrm{y}=\sqrt{\frac{1-\mathrm{x}}{\mathrm{x}}}$là

A. $0\le \mathrm{x}<1$

B. $0\le \mathrm{x}\le 1$

C. $0<\mathrm{x}\le 1$

D. $0<\mathrm{x}<1$

Câu 3: Tập nghiệm của bất phương trình $\frac{3{\mathrm{x}}^2+2\mathrm{x}-5}{{\left(\mathrm{x}+1\right)}^2}\le 0$là

A.$\left(-1;1\right)\cup \left(1;\frac{5}{3}\right)$

B. $\left[-\frac{5}{3};-1\right)\cup \left(-1;1\right]$

C. $\left[-1;1\right)\cup \left(1;\frac{5}{3}\right]$

D . $\left[-1;\frac{5}{3}\right]$

Câu 4:  Giá trị của m để bất phương trình luôn $\left(1-\mathrm{m}\right){\mathrm{x}}^2+\mathrm{x}-2\le 0$ đúng với mọi $\mathrm{x}\in \mathrm{ℝ}$ là                      

A. $\left[\frac{9}{8};+\infty \right)$                  

B. $\left(\frac{9}{8};1\right)\cup \left(1;+\infty \right)$                       

C. $\left(1;+\infty \right)$               

D. $\left(\frac{9}{8};1\right)$

I. Tự luận (8 điểm)

Câu 5:  (4 điểm) Giải các bất phương trình sau: 

$1)2{\mathrm{x}}^2+\mathrm{x}-\left|2\mathrm{x}+1\right|<0$

$2)\sqrt{2{\mathrm{x}}^2-3\mathrm{x}-5}\ge \mathrm{x}+1$

Câu 6:  (1 điểm) Tìm tất cả các giá trị của tham số a để bất phương trình  $-{\mathrm{x}}^2+4\mathrm{x}+5-\mathrm{a}<0$ với  $\forall \mathrm{x}<1$

Câu7: (2 điểm) Cho 2 điểm M(1;1), N(-2;3) và đường thẳng $\mathrm{\Delta }$ có phương trình: $2\mathrm{x}+\mathrm{y}-10=0$

1)  Xác định tọa độ điểm I thuộc đường thẳng $\mathrm{\Delta }$ sao cho tam giác MNI vuông tại M.

2)  Xác định tọa độ điểm K thuộc đường thẳng $\mathrm{\Delta }$ sao cho diện tích tam giác MNK bằng $\frac{29}{2}$ đvdt.

Câu 8: (1điểm) Cho $\mathrm{a}\ge -\frac{1}{2}$và$\frac{\mathrm{a}}{\mathrm{b}}>1$.  Chứng minh rằng$\frac{2{\mathrm{a}}^3+1}{4\mathrm{b}\left(\mathrm{a}-\mathrm{b}\right)}\ge 3$.

 Đáp án và thang điểm

I. Phần trắc nghiệm khách quan: (2 điểm - Mỗi câu 0,5 điểm)

Câu 1:   Chọn B

Ta có: $\cos \left(\mathrm{\Delta };{\mathrm{\Delta }}^{\text{'}}\right)=\frac{\left|\sqrt{3}.1+\left(-1\right).\left(-\sqrt{3}\right)\right|}{2.2}=\frac{\sqrt{3}}{2}$

Vậy góc giữa hai đường thẳng ${\text{Δ;Δ}}^{\text{'}}$ là $30°$.

Câu 2:   Chọn C

Hàm số y = $\sqrt{\frac{1-\mathrm{x}}{\mathrm{x}}}$ có nghĩa khi và chỉ khi $\left\{\begin{array}{l}\mathrm{x}\ne 0\\ \frac{1-\mathrm{x}}{\mathrm{x}}\ge 0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}\ne 0\\ 0<\mathrm{x}\le 1\end{array}\right.\iff 0<\mathrm{x}\le 1$

Câu 3:   Chọn B

Ta có: $\frac{3{\mathrm{x}}^2+2\mathrm{x}-5}{{\left(\mathrm{x}+1\right)}^2}\le 0\left(1\right)$ 

ĐKXĐ: x $\ne -1$

Vì ${\left(\mathrm{x}+1\right)}^2>0\forall \mathrm{x}\ne -1$

Nên BPT (1) $\iff 3{\mathrm{x}}^2+2\mathrm{x}-5\le 0$$\iff \frac{-5}{3}\le \mathrm{x}\le 1$

Kết hợp điều kiện, Vậy tập nghiệm của BPT đã cho là $\left[-\frac{5}{3};-1\right)\cup \left(-1;1\right]$.

Câu 4:   Chọn A

Bất phương trình $\left(1-\mathrm{m}\right){\mathrm{x}}^2+\mathrm{x}-2\le 0$ luôn đúng với mọi $\mathrm{x}\in \mathrm{ℝ}$ 

$\iff \left\{\begin{array}{l}1-\mathrm{m}<0\\ \mathrm{\Delta }\le 0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{m}>1\\ 9-8\mathrm{m}\le 0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{m}>1\\ \mathrm{m}\ge \frac{9}{8}\end{array}\right.\iff \mathrm{m}\ge \frac{9}{8}$

Vậy m $\in \left[\frac{9}{8};+\infty \right)$ thì thỏa mãn yêu cầu bài toán.

II. Phần tự luận

Câu 5.

1) Giải bất phương trình $2{\mathrm{x}}^2+\mathrm{x}-\left|2\mathrm{x}+1\right|<0$  $\left(1\right)$

Nếu $2\mathrm{x}+1\ge 0\iff \mathrm{x}\ge -\frac{1}{2}\left(*\right)$thì  $\left(1\right)$  $\iff 2{\mathrm{x}}^2-\mathrm{x}-1<0\iff -\frac{1}{2}<\mathrm{x}<1$

Kết hợp với điều kiện (*) ta có nghiệm của (1) là $-\frac{1}{2}<\mathrm{x}<1$     (0,75 điểm)

Nếu $2\mathrm{x}+1<0\iff \mathrm{x}<-\frac{1}{2}\left(**\right)$thì 

$\left(1\right)\iff$$2{\mathrm{x}}^2+\mathrm{x}+2\mathrm{x}+1<0$

$\iff 2{\mathrm{x}}^2+3\mathrm{x}+1<0\iff -1<\mathrm{x}<-\frac{1}{2}$

Kết hợp với điều kiện (**) thì (1) có nghiệm là $-1<\mathrm{x}<-\frac{1}{2}$ (0,75 điểm)

Vậy nghiệm của bất phương trình đã cho là $\left(-1;-\frac{1}{2}\right)\cup \left(-\frac{1}{2};1\right)$. (0,5 điểm)

2) Giải bất phương trình  $\sqrt{2{\mathrm{x}}^2-3\mathrm{x}-5}\ge \mathrm{x}+1$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}\mathrm{x}+1<0\\ 2{\mathrm{x}}^2-3\mathrm{x}-5\ge 0\end{array}\right.\left(1\right)\\ \left\{\begin{array}{l}\mathrm{x}+1\ge 0\\ 2{\mathrm{x}}^2-3\mathrm{x}-5\ge {\mathrm{x}}^2+2\mathrm{x}+1\end{array}\right.\left(2\right)\end{array}\right.$ (0,5 điểm)

Giải (1) $\iff \left\{\begin{array}{l}\mathrm{x}<-1\\ \left[\begin{array}{l}\mathrm{x}\le -1\\ \mathrm{x}\ge \frac{5}{2}\end{array}\right.\end{array}\right.\iff \mathrm{x}<-1$   (0,5 điểm)

Giải (2) $\iff \left\{\begin{array}{l}\mathrm{x}\ge -1\\ {\mathrm{x}}^2-5\mathrm{x}-6\ge 0\end{array}\right.$$\iff \left\{\begin{array}{l}\mathrm{x}\ge -1\\ \left[\begin{array}{l}\mathrm{x}\le -1\\ \mathrm{x}\ge 6\end{array}\right.\end{array}\right.\iff \mathrm{x}\ge 6$  (0,5 điểm)

Vậy tập nghiệm của bất phương trình đã cho là $\left(-\infty ;-1\right)\cup \left[6;+\infty \right)$. (0,5 điểm)

Câu 6.

Bất phương trình đã cho $\iff -{\mathrm{x}}^2+4\mathrm{x}+5<\mathrm{a}\left(*\right)$ với mọi x < 1

Gọi $\mathrm{f}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+4\mathrm{x}+5$ và g(x) = a thì $\mathrm{f}\left(\mathrm{x}\right)$ có bảng biến thiên

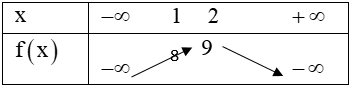(0,5 điểm)

Dựa vào bảng biến thiên nhận thấy (*) nghiệm đúng khi $\mathrm{f}\left(1\right)<\mathrm{a}\iff 8<\mathrm{a}$ (0,25 điểm)

Vậy với a > 8 thì BPT đã cho có nghiệm.  (0,25 điểm)

Câu 7.

1)

*Do $\mathrm{\Delta MNI}$ vuông tại M(1; 1) nên điểm I thuộc đường thẳng đi qua M và nhận $\overrightarrow{\mathrm{MN}}\left(-3;2\right)$ làm véc tơ pháp tuyến và có phương trình $-3\left(\mathrm{x}-1\right)+2\left(\mathrm{y}-1\right)=0$$\iff 3\mathrm{x}-2\mathrm{y}-1=0$ (0,5 điểm)

 *Mặt khác: Do điểm $\mathrm{I}\in \mathrm{\Delta }$nên toạ độ của I là nghiệm của hệ phương trình$\left\{\begin{array}{l}2\mathrm{x}+\mathrm{y}-10=0\\ 3\mathrm{x}-2\mathrm{y}-1=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=3\\ \mathrm{y}=4\end{array}\right.$  (0,25 điểm)

Vậy I(3;4). (0,25 điểm)

2) Do  ${\mathrm{S}}_{\mathrm{\Delta }\mathrm{MNK}}=\frac{1}{2}\mathrm{MN}.{\mathrm{d}}_{\left(\mathrm{K};\mathrm{MN}\right)}$: Trong đó $\mathrm{K}\in \mathrm{\Delta }\Rightarrow \mathrm{K}\left(\mathrm{b};-2\mathrm{b}+10\right)$

Đường thẳng MN $\overrightarrow{\mathrm{MN}}\left(-3;2\right)$ có véc tơ chỉ phương và đi qua  

M(1;1) $\Rightarrow$phương trình của đường thẳng MN là $2\mathrm{x}+3\mathrm{y}-5=0$  (0,25 điểm)

$\Rightarrow {\mathrm{d}}_{\left(\mathrm{K};\mathrm{M}\mathrm{N}\right)}=\frac{\left|-4\mathrm{b}+25\right|}{\sqrt{13}}$  ;   

$\mathrm{MN}=\left|\overrightarrow{\mathrm{MN}}\right|=\sqrt{13}$, ${\mathrm{S}}_{\mathrm{\Delta MNK}}=\frac{29}{2}$

Ta có $\frac{29}{2}=\frac{1}{2}\sqrt{13}\frac{\left|-4\mathrm{b}+25\right|}{\sqrt{13}}\iff \left|-4\mathrm{b}+25\right|=29\iff \left[\begin{array}{l}\mathrm{b}=-1\\ \mathrm{b}=\frac{27}{2}\end{array}\right.$    (0,25 điểm)

Với    $\mathrm{b}=-1\Rightarrow \mathrm{K}(-1;12)$

Với    $\mathrm{b}=\frac{27}{2}\Rightarrow \mathrm{K}\left(\frac{27}{2};-17\right)$               (0,25 điểm)

Vậy có 2 điểm K thỏa mãn bài ra là K(-1;12) và K$\left(\frac{27}{2};-17\right)$. (0,25 điểm)

Câu 8.

Do $\frac{\mathrm{a}}{\mathrm{b}}>1\iff \frac{\mathrm{a}-\mathrm{b}}{\mathrm{b}}>0\Rightarrow \mathrm{b}\left(\mathrm{a}-\mathrm{b}\right)>0$

Và ${\left(\mathrm{a}-2\mathrm{b}\right)}^2\ge 0\iff {\mathrm{a}}^2-4\mathrm{ab}+4{\mathrm{b}}^2\ge 0\iff 4\mathrm{b}\left(\mathrm{a}-\mathrm{b}\right)\le {\mathrm{a}}^2\left(1\right)$  (0,25 điểm)

$$\begin{gathered} \mathrm{a}\ge -\frac{1}{2}\iff 2\mathrm{a}+1\ge 0 \\ \iff \left(2\mathrm{a}+1\right){\left(\mathrm{a}-1\right)}^2\ge 0 \\ \iff 2{\mathrm{a}}^3+1-3{\mathrm{a}}^2\ge 0 \end{gathered}$$

$\iff \frac{2{\mathrm{a}}^3+1}{3}\ge {\mathrm{a}}^2\left(2\right)$  (0,25 điểm)

Từ (1) và (2)$\Rightarrow 4\mathrm{b}\left(\mathrm{a}-\mathrm{b}\right)\le {\mathrm{a}}^2\le \frac{2{\mathrm{a}}^3+1}{3}$

$\Rightarrow 4\mathrm{b}\left(\mathrm{a}-\mathrm{b}\right)-3\le \frac{2{\mathrm{b}}^3+1}{3}$  (0,25 điểm)

$\text{⇔}\frac{2a^3+1}{4b(a-b)}\ge 3$  (đpcm). (0,25 điểm)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa học kì 2

Năm học 2021 - 2022

Môn: Toán 10

Thời gian làm bài: 45 phút

Đề thi Giữa học kì 2 Toán lớp 10 Trắc nghiệm + Tự luận năm 2022 đề số 2

I. Trắc nghiệm (2 điểm)

Hãy chọn phương án trả lời đúng cho mỗi câu sau:

Câu 1: Cho 2 đường thẳng$\mathrm{\Delta }$và $\mathrm{\Delta }\text{'}$lần lượt có phương trình là x + 2y - 1 = 0

và 3x + y + 6 = 0. Góc giữa 2 đường thẳng $\mathrm{\Delta }$ và $\mathrm{\Delta }\text{'}$là:

A. $60°$                             

B. $45°$                             

C. $0°$                     

D. $135°$

Câu 2: Điều kiện xác định của hàm số $\mathrm{y}=\sqrt{\frac{\mathrm{x}}{1-\mathrm{x}}}$là

A. $0\le \mathrm{x}<1$                      

B. $0\le \mathrm{x}\le 1$                      

C. $0<\mathrm{x}\le 1$            

D. $0<\mathrm{x}<1$

Câu 3: Tập nghiệm của bất phương trình $\frac{3{\mathrm{x}}^2-2\mathrm{x}-5}{{\left(\mathrm{x}-1\right)}^2}\le 0$là

A. $\left(-1;1\right)\cup \left(1;\frac{5}{3}\right)$            

B. $\left(1;\frac{5}{3}\right]$                          

C. $\left[-1;1\right)\cup \left(1;\frac{5}{3}\right]$           

D. $\left[-1;\frac{5}{3}\right]$

Câu 4: Giá trị của m để bất phương trình $\left(\mathrm{m}-2\right){\mathrm{x}}^2+2\mathrm{x}+2\ge 0$luôn đúng với mọi $\mathrm{x}\in \mathrm{ℝ}$ là

A. $\left[\frac{5}{2};+\infty \right)\cup \left\{2\right\}$            

B. $\left[2;+\infty \right)$                        

C. $\left[\frac{5}{2};+\infty \right)$                      

D. $\left[1;\frac{3}{2}\right)\cup \left(2;+\infty \right)$

II. Tự luận (8 điểm)

Câu 5: (4 điểm) Giải các bất phương trình sau:

$1){\mathrm{x}}^2+2\mathrm{x}-\left|\mathrm{x}+2\right|<0$

$2)\sqrt{2{\mathrm{x}}^2-5\mathrm{x}+3}\ge \mathrm{x}-1$

Câu 6:  (1 điểm) Tìm tất cả các giá trị của tham số m để bất phương trình${\mathrm{x}}^2+4\mathrm{x}+3-\mathrm{m}\ge 0$ với $\forall \mathrm{x}>1$.

Câu 7: (2 điểm) Cho 2 điểm A(-1;1), B(3;7) và đường thẳng d có phương trình: $\mathrm{x}+2\mathrm{y}+1=0$

1) Xác định tọa độ điểm C thuộc đường thẳng d sao cho tam giác ABC vuông tại A.

2) Xác định tọa độ điểm D thuộc đường thẳng d sao cho diện tích tam giác ABD bằng 50.

Câu 8: (1điểm) Cho $\mathrm{b}\ge -\frac{1}{2}$và$\frac{\mathrm{b}}{\mathrm{a}}>1$.  Chứng minh rằng   $\frac{2{\mathrm{b}}^3+1}{4\mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)}\ge 3$.

 Đáp án và thang điểm

I. Phần trắc nghiệm khách quan: (2 điểm - Mỗi câu 0,5 điểm)

Câu 1:  Chọn B

Ta có: $\cos \left({\mathrm{\Delta }}_1;{\mathrm{\Delta }}_2\right)=\frac{\left|1.3+2.1\right|}{\sqrt{1+2^2}.\sqrt{1+3^2}}=\frac{\sqrt{2}}{2}$

Suy ra góc giữa hai đường thẳng ${\mathrm{\Delta }}_1;{\mathrm{\Delta }}_2$ là $45°$.

Câu 2:  Chọn A

Hàm số $\mathrm{y}=\sqrt{\frac{\mathrm{x}}{1-\mathrm{x}}}$ có nghĩa khi 

$\left\{\begin{array}{l}1-\mathrm{x}\ne 0\\ \frac{\mathrm{x}}{1-\mathrm{x}}\ge 0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}\ne 1\\ 0\le \mathrm{x}<1\end{array}\right.\iff 0\le \mathrm{x}<1$

Câu 3:  Chọn C

Ta có: $\frac{3{\mathrm{x}}^2-2\mathrm{x}-5}{{\left(\mathrm{x}-1\right)}^2}\le 0$ (1)

ĐKXĐ: x $\ne$1

Vì ${\left(\mathrm{x}-1\right)}^2>0$ với mọi x $\ne$1

Nên BPT (1)$\iff 3{\mathrm{x}}^2-2\mathrm{x}-5\le 0$ $\iff -1\le \mathrm{x}\le \frac{5}{3}$

Kết hợp điều kiện, Vậy tập nghiệm của BPT đã cho là S = $\left[-1;1\right)\cup \left(1;\frac{5}{3}\right]$.

Câu 4:  Chọn C

Bất phương trình$\left(\mathrm{m}-2\right){\mathrm{x}}^2+2\mathrm{x}+2\ge 0$ luôn đúng với mọi x $\in \mathrm{ℝ}$ khi và chỉ khi

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{m}-2>0\\ {\mathrm{\Delta }}^{\text{'}}\le 0\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{m}>2\\ 1^2-\left(\mathrm{m}-2\right).2\le 0\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{m}>2\\ \mathrm{m}\ge \frac{5}{2}\end{array}\right.\iff \mathrm{m}\ge \frac{5}{2} \end{gathered}$$

Vậy m $\in \left[\frac{5}{2};+\infty \right)$ thì thỏa mãn yêu cầu bài toán.

II. Phần tự luận

Câu 5.

1) Giải bất phươmg trình ${\mathrm{x}}^2+2\mathrm{x}-\left|\mathrm{x}+2\right|<0\left(1\right)$

Nếu $\mathrm{x}+2\ge 0\iff \mathrm{x}\ge -2\left(*\right)$ thì    

$\left(1\right)\iff$${\mathrm{x}}^2+2\mathrm{x}-\mathrm{x}-2<0$ 

$\iff {\mathrm{x}}^2+\mathrm{x}-2<0\iff -2<\mathrm{x}<1$

Kết hợp với điều kiện (*) ta có:    $-2<\mathrm{x}<1$       (0,75 điểm)

Nếu $\mathrm{x}+2<0\iff \mathrm{x}<-2\left(**\right)$thì  $\left(1\right)\iff$${\mathrm{x}}^2+2\mathrm{x}+\mathrm{x}+2<0$ 

$\iff {\mathrm{x}}^2+3\mathrm{x}+2<0\iff -2<\mathrm{x}<-1$

Kết hợp với điều kiện (**) thì (1) vô nghiệm     (0,75 điểm)

Vậy nghiệm của bất phương trình đã cho là $-2<\mathrm{x}<1$.             (0,5 điểm)

2) Giải bất phương trình  $\sqrt{2{\mathrm{x}}^2-5\mathrm{x}+3}\ge \mathrm{x}-1$

Ta có: $\sqrt{2{\mathrm{x}}^2-5\mathrm{x}+3}\ge \mathrm{x}-1$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}\mathrm{x}-1<0\\ 2{\mathrm{x}}^2-5\mathrm{x}+3\ge 0\end{array}\right.\left(1\right)\\ \left\{\begin{array}{l}\mathrm{x}-1\ge 0\\ 2{\mathrm{x}}^2-5\mathrm{x}+3\ge {\mathrm{x}}^2-2\mathrm{x}+1\end{array}\right.\left(2\right)\end{array}\right.$      (0,5 điểm)

Giải (1) $\iff \left\{\begin{array}{l}\mathrm{x}<1\\ \left[\begin{array}{l}\mathrm{x}\le 1\\ \mathrm{x}\ge \frac{3}{2}\end{array}\right.\end{array}\right.\iff \mathrm{x}<1$   (0,5 điểm)

 Giải (2) $\text{⇔}\left\{\begin{array}{l}\mathrm{x}\ge 1\\ {\mathrm{x}}^2-3\mathrm{x}+2\ge 0\end{array}\right.$

$\iff \left\{\begin{array}{l}\mathrm{x}\ge 1\\ \left[\begin{array}{l}\mathrm{x}\le 1\\ \mathrm{x}\ge 2\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}\mathrm{x}=1\\ \mathrm{x}\ge 2\end{array}\right.$(0,5 điểm)

Vậy tập nghiệm của bất phương trình đã cho là $\left(-\infty ;1\right]\cup \left[2;+\infty \right)$. (0,5 điểm)

Câu 6.

Bất phương trình đã cho $\iff {\mathrm{x}}^2+4\mathrm{x}+3\ge \mathrm{m}\left(*\right)$ với mọi x >1

Gọi $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2+4\mathrm{x}+3$ và g(x) = m thì g(x) có đồ thị là đường thẳng

còn  $\mathrm{f}\left(\mathrm{x}\right)$ có bảng biến thiên

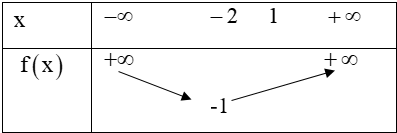 (0,5 điểm)

Dựa vào bảng biến thiên nhận thấy (*) đúng khi f(1) > m $\iff \mathrm{m}<8$ (0,25 điểm)

Vậy với $\mathrm{m}<8$ thì BPT đã cho có nghiệm. (0,25 điểm)

Câu 7.

1) Cho 2 điểm A(-1;1), B(3;7) và đường thẳng d có phương trình: $\mathrm{x}+2\mathrm{y}+1=0$.  Xác định tọa độ điểm C thuộc đường thẳng d sao cho tam giác ABC vuông tại A.

*Do $\mathrm{\Delta ABC}$ vuông tại A(-1; 1) nên điểm C thuộc đường thẳng đi qua A và nhận $\overrightarrow{\mathrm{AB}}\left(4;6\right)$ làm véc tơ pháp tuyến và có phương trình $4\left(\mathrm{x}+1\right)+6\left(\mathrm{y}-1\right)=0$

$\iff 2\mathrm{x}+3\mathrm{y}-1=0$(0,5 điểm)

 *Mặt khác: Do điểm $\mathrm{C}\in \mathrm{d}$nên toạ độ của C là nghiệm của hệ phương trình

$\left\{\begin{array}{l}2\mathrm{x}+3\mathrm{y}-1=0\\ \mathrm{x}+2\mathrm{y}+1=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=5\\ \mathrm{y}=-3\end{array}\right.$  (0,25 điểm)

 Vậy C(5;-3). (0,25 điểm)

2) Cho 2 điểm A(-1; 1), B(3; 7) và đường thẳng d có phương trình:  $\mathrm{x}+2\mathrm{y}+1=0$. Xác định tọa độ điểm D thuộc đường thẳng d sao cho diện tích tam giác ABD bằng 50.

Do ${\mathrm{S}}_{\mathrm{ABD}}=\frac{1}{2}\mathrm{AB}.{\mathrm{d}}_{\left(\mathrm{D};\mathrm{AB}\right)}$  

Trong đó $\mathrm{D}\in \mathrm{d}\Rightarrow \mathrm{D}\left(-1-2\mathrm{a};\mathrm{a}\right)$

Đường thẳng AB có véc tơ chỉ phương $\overrightarrow{\mathrm{AB}}\left(4;6\right)$ và đi qua A(-1;1)

$\Rightarrow$phương trình  của đường thẳng AB là $3\mathrm{x}-2\mathrm{y}+5=0$   (0,25 điểm)

$\Rightarrow {\mathrm{d}}_{\left(\mathrm{D};\mathrm{AB}\right)}=\frac{\left|-8\mathrm{a}+2\right|}{\sqrt{13}}$  ;   

$\mathrm{AB}=\left|\overrightarrow{\mathrm{AB}}\right|=\sqrt{52}$, ${\mathrm{S}}_{\mathrm{\Delta ABD}}=50$  

Ta có

$50=\frac{1}{2}.\sqrt{52}.\frac{\left|-8\mathrm{a}+2\right|}{\sqrt{13}}$

$\iff \left|-8\mathrm{a}+2\right|=50\iff \left[\begin{array}{l}\mathrm{a}=-6\\ \mathrm{a}=\frac{13}{2}\end{array}\right.$    (0,25 điểm)

Với    $\mathrm{a}=-6\Rightarrow \mathrm{D}(11;-6)$ (0,25 điểm)

Với    $\mathrm{a}=\frac{13}{2}\Rightarrow \mathrm{D}\left(-14;\frac{13}{2}\right)$  (0,25 điểm)

Câu 8. Cho $\mathrm{b}\ge -\frac{1}{2}$và $\frac{\mathrm{b}}{\mathrm{a}}>1$.  Chứng minh rằng   $\frac{2{\mathrm{b}}^3+1}{4\mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)}\ge 3$.

Giải:

Do $\frac{\mathrm{b}}{\mathrm{a}}>1\iff \frac{\mathrm{b}-\mathrm{a}}{\mathrm{a}}>0\Rightarrow \mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)>0$

Và ${\left(\mathrm{b}-2\mathrm{a}\right)}^2\ge 0\iff {\mathrm{b}}^2-4\mathrm{ba}+4{\mathrm{a}}^2\ge 0$

$\iff 4\mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)\le {\mathrm{b}}^2\left(1\right)$     (0,25 điểm)

$\mathrm{b}\ge -\frac{1}{2}\iff 2\mathrm{b}+1\ge 0\iff \left(2\mathrm{b}+1\right){\left(\mathrm{b}-1\right)}^2\ge 0$

$\iff 2{\mathrm{b}}^3+1-3{\mathrm{b}}^2\ge 0\iff \frac{2{\mathrm{b}}^3+1}{3}\ge {\mathrm{b}}^2\left(2\right)$ (0,25 điểm)

Từ (1) và (2)$\Rightarrow 4\mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)\le {\mathrm{b}}^2\le \frac{2{\mathrm{b}}^3+1}{3}$

$\Rightarrow 4\mathrm{a}\left(\mathrm{b}-\mathrm{a}\right)\le \frac{2{\mathrm{b}}^3+1}{3}$  (0,25 điểm)

$\iff \frac{2{\mathrm{b}}^3+1}{4\mathrm{a}(\mathrm{b}-\mathrm{a})}\ge 3$  (đpcm)         (0,25 điểm)