[Năm 2022] Đề thi Giữa học kì 12 Toán lớp 10 có đáp án (6 đề)
6 Đề thi Giữa học kì 2 Toán lớp 10 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 10 Giữa học kì 2. Mời các bạn cùng đón xem:
[Năm 2022] Đề thi Giữa học kì 12 Toán lớp 10 có đáp án (6 đề)
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
[Năm 2022] Đề thi Giữa học kì 12 Toán lớp 10 có đáp án đề số 1
I.TRẮC NGHIỆM (7 điểm)
Câu 1: Trong mặt phẳng Oxy cho hai đường thẳng d1:x+3y−1=0và d1:2x+6y−5=0. Xét vị trí tương đối của hai đường thẳng d1và d2
A. Song song với nhau.
B. Vuông góc nhau.
C. Cắt nhau nhưng không vuông góc.
D. Trùng nhau.
Câu 2: Xét tam giác ABC tùy ý có BC = a,AC=b,AB =c mệnh đề nào sau đây đúng?
A. a2=b2+c2−bc.cosA.
B. a2=b2+c2+2bc.cosA
C. a2=b2+c2−2bc.cosA.
D. a2=b2+c2+bc.cosA
Câu 3: Hàm số có kết quả xét dấu
|
x |
−∞ 2 +∞ |
|
f(x) |
+ 0 − |
là hàm số nào trong các hàm số sau?
A. f(x)=x−1
B. f(x)=x−2
C. f(x)=−x+2
D. f(x)=−x2+4x−4
Câu 4: Xét tam thức bậc hai f(x)=ax2+bx+c có Δ=b2−4ac.Điều kiện cần và đủ để f(x)<0,∀x∈ℝ là
A. {a>0Δ<0.
B. {a>0Δ≤0.
C. {a<0Δ<0.
D. {a<0Δ≤0.
Câu 5: Điều kiện xác định của bất phương trình 3√3x+7−x>x2+3 là:
A. x>−73.
B. x<−73.
C. x≥−73.
D. x≠−73.
Câu 6: Cho biểu thức f(x)=ax+b,a≠0. Dấu của f(x) trên khoảng (−ba;+∞)
A. dương.
B. âm.
C. trái dấu với a.
D. cùng dấu với a.
Câu 7: Tập nghiệm của hệ bất phương trình {4−x>03x+1>2x−2 là:
A. S=[−3;4].
B. S=(−∞; 4).
C. S=(−3; 4).
D. S=(−3; +∞).
Câu 8: Số x = 1 là nghiệm của bất phương trình nào sau đây:
A. 4x−11>x.
B. 2x−1>3.
C. 3x+2<4.
D. 2x−3<0.
Câu 9: Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng có phương trình {x=1+3ty=3−2t.
A. (3;2).
B. (3;−2).
C. (2;−3).
D. (2;3).
Câu 10: Xét tam thức bậc hai f(x)=ax2+bx+c có Δ=b2−4ac.Điều kiện cần và đủ để f(x)≥0,∀x∈ℝ là:
A. {a<0Δ<0.
B. {a>0Δ≤0.
C. {a>0Δ<0.
D. {a<0Δ≤0.
Câu 11: Tam giác ABC có góc A bằng 450 và độ dài cạnh BC bằng a. Bán kính đường tròn ngoại tiếp tam giác ABC là:
A. a√32.
B. a√3.
C. a√22.
D. a√2.
Câu 12: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 1.
B. 3.
C. 2.
D. Vô số.
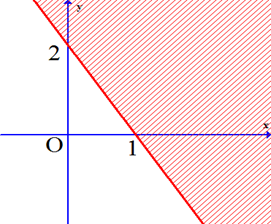
Câu 13: Biểu diễn miền nghiệm ( miền không gạch chéo) được cho bởi hình bên là miền nghiệm của bất phương trình nào ?
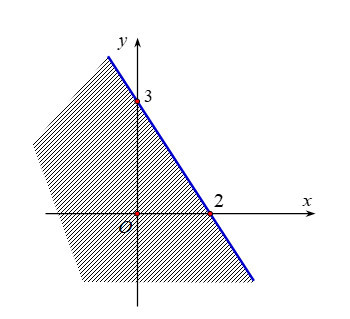
A. 3x+2y≤6.
B. 3x+2y≥6.
C. 2x+3y≥6.
D. 3x+2y+6>0.
Câu 14: Cho tam thức bậc hai f(x)=−x2+4x−3. Mệnh đề nào dưới đây đúng ?
A. f(x)>0,∀x∈(1;3).
B. f(x)<0,∀x∈(1;3).
C. f(x)>0,∀x∈(−∞;1)∪(3;+∞).
D. f(x)<0,∀x∈ℝ.
Câu 15: Tìm điều kiện xác định của bất phương trình 23−x+x≥1
A. x≠3.
B. x=3.
C. x>3.
D. x<3.
Câu 16: Cho tam thức bậc hai có bảng xét dấu như sau
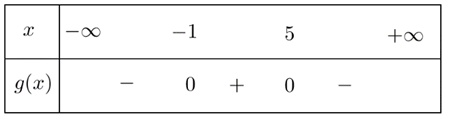
Mệnh đề nào dưới đây đúng?
A. g(x) có Δ < 0, a < 0.
B. g(x) có Δ > 0, a < 0.
C. g(x) có Δ > 0, a > 0.
D. g(x) có Δ = 0, a < 0.
Câu 17: Biểu thức nào sau đây là nhị thức bậc nhất?
A. f(x) = 3x + 5.
B. f(x) = 4x2 – 3x + 1.
C. f(x, y) = 2x – 3y – 1.
D. f(x) = 2021
Câu 18: Xét tam giác ABC tùy ý có BC = a, AC = b, AB = c, đường tròn ngoại tiếp tam giác có bán kính R.Diện tích tam giác ABC bằng:
A. S=abcR.
B. S=abc2R.
C. S=4abcR .
D. S=abc4R.
Câu 19: Cặp số (x0;y0) nào là nghiệm của bất phương trình 4x+4y≥3.
A. (x0;y0) = (0;0)
B. (x0;y0) = (-1;-1)
C. (x0;y0) = (-2;-2)
D. (x0;y0) = (1;1)
Câu 20: Cho tam thức bậc hai f(x) = 9x2 – 6x + 1. Xét dấu f(x) ta có kết quả:
A. f(x)<0,∀x∈(−∞;13).
B. f(x)≥0,∀x∈ℝ.
C. f(x)>0,∀x∈ℝ.
D. f(x)≤0,∀x∈ℝ.
Câu 21: Viết phương trình tổng quát của đường thẳng d đi qua điểm A(1;3) và có vectơ pháp tuyến →n=(3;2)
A. 3x+2y−9=0.
B. 3x+2y−6=0.
C. 3x+2y−7=0.
D. 3x+2y−8=0.
II.TỰ LUẬN(3 điểm)
Bài 1(1 điểm):Giải bất phương trình (3x+5)(2021−4x)(√5x−3).x≥0
Bài 2(1 điểm):Tìm tất cả các giá trị thực của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x dương: (m2−1)x2−2(m−1)x−1<0.
Bài 3 (1 điểm): Trong mặt phẳng (Oxy) cho điểm M(2;4) và d:{x=1−3ty=2+t . Viết phương trình đường thẳng D song song với đường thẳng d và cách điểm M một khoảng bằng √10.
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
ĐA |
A |
C |
C |
C |
A |
D |
C |
D |
B |
B |
C |
|
Câu |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
|
ĐA |
D |
B |
A |
A |
B |
A |
D |
D |
B |
A |
|
Giải chi tiết:
Câu 1: Ta có: aa'
Do đó d1 // d2
Chọn A.
Câu 2: Theo định lý cos, ta có: .
Chọn C
Câu 3: Dựa vào bảng xét dấu, ta có: f(x) là hàm nhị thức bậc nhất, f(x) = 0 khi x = 2 và hệ số a < 0.
Xem xét tất cả đáp án ta thấy f(x) = - x + 2 là đa thức thỏa mãn.
Chọn C.
Câu 4: Điều kiện cần và đủ để là: .
Chọn C
Câu 5: Điều kiện xác định của bất phương trình là: 3x + 7 > 0
Chọn A
Câu 6: là nhị thức bậc nhất. Khi đó:
- cùng dấu với hệ số a trên khoảng ;
- f(x) trái dấu với hệ số a trên khoảng ;
- f(x) = 0 khi .
Chọn D.
Câu 7: Ta có:
Vậy tập nghiệm của hệ phương trình là: .
Chọn C.
Câu 8: Thay x = 1 vào từng bất phương trình ở các đáp án, ta được:
Đáp án A: 4.1 – 11 > 1 ⇔ - 7 > 1 (vô lí).
Đáp án B. 2.1 – 1 > 3 ⇔ 1 > 3 (vô lí).
Đáp án C. 3.1 + 2 < 4 ⇔ 5 < 4 (vô lí).
Đáp án D. 2.1 – 3 < 3 ⇔ - 1 < 3 (luôn đúng).
Chọn D.
Câu 9: Vectơ chỉ phương của đường thẳng có phương trình là (3;-2).
Chọn B
Câu 10: Điều kiện cần và đủ để là: .
Chọn B
Câu 11: Xét tam giác ABC có:
.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là .
Chọn C
Câu 12: Một đường thẳng có vô số vectơ pháp tuyến.
Chọn D
Câu 13: Đường thẳng biên là: . Do đó loại C và D
Quan sát hình vẽ, ta thấy: điểm (0;0) không thuộc vào miền nghiệm của bất phương trình đã cho nên ta thay x = 0, y = 0 vào đáp án A và đáp án B, đáp án nào không thỏa mãn sẽ là bất phương trình cần tìm:
Đáp án A: (luôn đúng).
Đáp án B: (vô lí).
Chọn B
Câu 14: Cho tam thức bậc hai
Ta có: - x2 + 4x – 3 = 0
Áp dụng định lý dấu tam thức bậc hai, ta có: .
Chọn A
Câu 15: Điều kiện xác định của bất phương trình là .
Chọn A
Câu 16: Dựa vào bảng xét dấu, ta có: g(x) có hai nghiệm phân biệt (tương đương với Δ > 0) và hệ số a < 0.
Chọn B
Câu 17: Nhị thức bậc nhất là: f(x) = 3x + 5.
Chọn A
Câu 18: Diện tích tam giác ABC là: .
Chọn D
Câu 19: Cặp số (x0;y0) nào là nghiệm của bất phương trình .
Đáp án A: Thay x0 = 0 và y0 = 0 vào bất đẳng thức đã cho ta được:
(vô lí)
Vậy (0;0) không là nghiệm của BPT đã cho.
Đáp án B: Thay x0 = -1 và y0 = -1 vào bất đẳng thức đã cho ta được:
(vô lí)
Vậy (-1;-1) không là nghiệm của BPT đã cho.
Đáp án C: Thay x0 = -2 và y0 = -2 vào bất đẳng thức đã cho ta được:
(vô lí)
Vậy (-2;-2) không là nghiệm của BPT đã cho.
Đáp án D: Thay x0 = 1 và y0 = 1 vào bất đẳng thức đã cho ta được:
(thỏa mãn)
Vậy (1;1) là nghiệm của BPT đã cho.
Chọn D
Câu 20: Ta có: f(x) = 9x2 – 6x + 1 = (3x – 1)2 ≥ 0 .
Chọn B
Câu 21: Phương trình tổng quát của đường thẳng d đi qua điểm A(1;3) và có vectơ pháp tuyến là: 3(x – 1) + 2(y – 3) = 0 ⇔ 3x + 2y – 9 = 0.
Chọn A
II. PHẦN TỰ LUẬN
|
Bài |
Nội dung yêu cầu |
Điểm |
|
Bài 1 |
Giải bất phương trình |
(1,0đ) |
|
(1đ) |
Giải được từng nghiệm của mỗi nhị thức
|
0,25 |
|
Lập đúng bảng xét dấu: 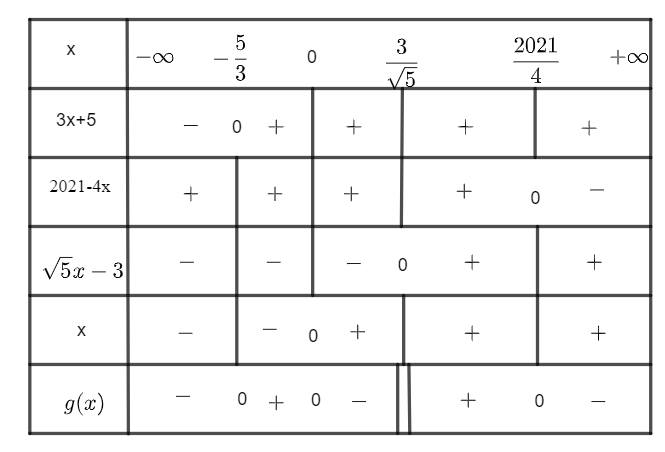 (Nếu học sinh dùng bảng xét dấu 2 dòng thì phải giải thích việc chọn dấu trong các khoảng). |
0,5 |
|
|
Kết luận đúng tập nghiệm |
0,25 |
|
|
Bài 2 |
Tìm tất cả các giá trị thực của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x dương.
|
(1,0đ) |
|
(1,0đ) |
TH1: * m = 1, , thỏa mãn. *, , không thỏa mãn. |
0,25 |
|
TH2: , |
|
|
|
Khi đó, xảy ra trong các trường hợp sau: |
|
|
|
1. |
0,25 |
|
|
2. |
0,25 |
|
|
KL: |
0,25 |
|
|
Bài 3 |
Trong mặt phẳng Oxy cho điểm và Viết PT ĐT D song song với đường thẳng d và cách điểm M một khoảng bằng . |
(1,0đ) |
|
(1,0đ)
Bài 3 |
Xác định được vecto chỉ phương của đường thẳng d: Suy ra VTPT của đường thẳng d: |
0,25 |
|
Vì đường thẳng D song song với đường thẳng d nên VTPT của đường thẳng D là: PT ĐT D có dạng: |
0,25 |
|
|
|
0,25 |
|
|
(Thỏa mãn điều kiện) |
|
|
|
KL : Vậy hai phương trình D cần tìm là: |
0,25 |
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2021 - 2022
Môn: Toán 10
Thời gian làm bài: 45 phút
[Năm 2022] Đề thi Giữa học kì 12 Toán lớp 10 có đáp án đề số 2
I. PHẦN TRẮC NGHIỆM (4 điểm)
Câu 1: Tìm góc giữa 2 đường thẳng Δ1: 2x – y – 10 = 0 và Δ2: x – 3y – 9 = 0:
A.
B.
C.
D.
Câu 2: Tập nghiệm của bất phương trình
A.
B.
C.
D.
Câu 3: Véctơ nào sau đây là một véctơ pháp tuyến của đường thẳng – x + 3y + 2 = 0?
A. .
B. .
C. .
D. .
Câu 4: Tính khoảng cách d từ điểm A(1;2) đến đường thẳng Δ: 12x + 5y + 4 = 0.
A. .
B. .
C. .
D. .
Câu 5: Hệ bất phương trình có tập nghiệm là :
A.
B.
C.
D.
Câu 6: Tập nghiệm của bất phương trình
A.
B.
C.
D. .
Câu 7: Nhị thức nhận giá trị âm với mọi x thuộc tập hợp nào?
A. .
B. .
C. .
D. .
Câu 8: Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Câu 9: Tập nghiệm của bất phương trình là
A.
B.
C.
D.
Câu 10: Bất phương trình xác định khi nào?
A.
B.
C.
D.
Câu 11: Biểu diễn miền nghiệm được cho bởi hình bên là miền nghiệm của bất phương trình nào ?
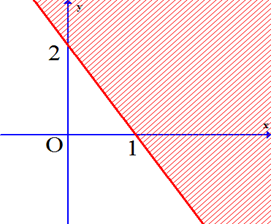
A.
B.
C.
D.
Câu 12: Biểu thức nào sau đây có bảng xét dấu như:

A.
B. .
C.
D.
Câu 13: Cho bảng xét dấu:

Biểu thức là biểu thức nào sau đây?
A.
B.
C.
D.
Câu 14: Cặp số là nghiệm của bất phương trình
A.
B.
C.
D.
Câu 15: Đường thẳng nào qua A(2;1) và song song với đường thẳng: 2x + 3y – 2 = 0?
A.
B.
C.
D.
Câu 16: Tam thức nhận giá trị dương khi chỉ khi:
A.
B. .
C. .
D. .
Câu 17: Nhị thức nhận giá trị dương với mọi x thuộc tập hợp nào?
A. .
B. .
C. .
D. .
Câu 18: Cho phương trình đường thẳng . Véctơ nào sau đây là một véctơ chỉ phương của đường thẳng d?
A.
B.
C.
D.
Câu 19: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP =(3;–4) là
A.
B.
C.
D.
Câu 20: Cho 2 điểm A(1;−4) , B(3;2). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB.
A.
B.
C.
D.
II. PHẦN TỰ LUẬN (6 điểm)
Câu 21. (3 điểm) Giải các bất phương trình sau:
a)
b)
c)
Câu 22. (1 điểm) Cho phương trình : , với m là tham số.
Tìm tất cả các giá trị của m để phương trình có hai nghiệm trái dấu
Câu 23 . (2 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm và
a) Viết phương trình đường thẳng AB (0.75 điểm)
b) Tính khoảng cách từ điểm M đến đường thẳng (0.75 điểm)
c) Viết phương trình đường thẳng d, biết d đi qua điểm A và cắt tia Ox,Oy thứ tự tại C,N sao cho tam giác OCN có diện tích nhỏ nhất. (0.5 điểm)
ĐÁP ÁN – HƯỚNG DẪN CHẤM KIỂM TRA GIỮA KÌ 2 TOÁN 10
I. PHẦN TRẮC NGHIỆM (4 điểm) Mỗi đáp án đúng chấm 0.2 điểm
|
1 |
B |
6 |
D |
11 |
A |
16 |
C |
|
2 |
C |
7 |
A |
12 |
A |
17 |
C |
|
3 |
A |
8 |
D |
13 |
D |
18 |
D |
|
4 |
B |
9 |
B |
14 |
C |
19 |
B |
|
5 |
B |
10 |
D |
15 |
C |
20 |
A |
Giải chi tiết:
Câu 1: Ta có: Δ1: 2x – y – 10 = 0 có VTPT
Δ2: x – 3y – 9 = 0 có VTPT
khi đó, ta có: cos(Δ1,Δ2) =
Suy ra góc giữa hai đường thẳng Δ1 và Δ2 là: 450.
Chọn B.
Câu 2:
Ta có: - 4x2 – 4x + 24 = 0
Áp dụng định lý dấu của tam thức bậc hai ta có:
Vậy tập nghiệm của bất phương trình là:
Chọn C
Câu 3: Véctơ pháp tuyến của đường thẳng – x + 3y + 2 = 0 là .
Chọn A
Câu 4: Khoảng cách từ điểm A đến đường thẳng Δ là:
.
Chọn B
Câu 5: Ta có:
Vậy tập nghiệm của hệ phương trình:
Chọn B
Câu 6:
Vì nên và
Vậy tập nghiệm của BPT là: .
Chọn D
Câu 7: Nhị thức f(x) = -2x + 4 < 0 ⇔ x > 2.
Vậy nhị thức f(x) nhận giá trị âm khi x .
Chọn A
Câu 8: Ta có:
⇔ 2x – 4 > 3x + 9
⇔ x < - 13
Vậy tập nghiệm của BPT đã cho là:
Chọn D
Câu 9:
+) TH1:
Khi đó BPT trở thành: x – 2 < 1 ⇔ x < 3 .
Kết hợp với điều kiện ta được: (1).
+) TH2: x – 2 < 0 ⇔ x < 2
Khi đó BPT trở thành: - x + 2 < 1 ⇔ x > 1
Kết hợp với điều kiện ta được: 1 < x < 2 (2).
Từ (1) và (2) suy ra: 1 < x < 3
Vậy tập nghiệm của BPT là: S = (1;3).
Chọn B
Câu 10: Điều kiện xác định của bất phương trình:
Chọn D
Câu 11:
 Ta có điểm (0;0) thuộc vào miền nghiệm nên nó là nghiệm của BPT đã cho.
Ta có điểm (0;0) thuộc vào miền nghiệm nên nó là nghiệm của BPT đã cho.
Thay x = 0, y = 0 vào các đáp án, ta được:
Đáp án A. 2.0 + 0 – 2 ≤ 0 ⇔ - 2 ≤ 0 (luôn đúng)
Đáp án B. 2.0 + 0 – 2 > 0 ⇔ - 2 > 0 (vô lí)
Đáp án C. 2.0 + 0 – 1 > 0 ⇔ - 1 > 0 (vô lí)
Đáp án D. 2.0 + 0 + 2 ≤ 0 ⇔ 2 ≤ 0 (vô lí)
Chọn A
Câu 12: Dựa vào bảng xét dấu, ta có: f(x) là nhị thức bậc nhất và f(x) = 0 khi x = 5, hơn nữa hệ số a > 0.
Do đó chỉ có đáp án A thỏa mãn.
Chọn A
Câu 13: Cho bảng xét dấu:

Dựa vào bảng xét dấu, ta có: f(x), g(x) là các nhị thức bậc nhất.
f(x) = 0 khi x = 6 và hệ số a > 0 ⇒ f(x) = x – 6;
g(x) = 0 khi và hệ số a < 0 ⇒ g(x) = - 2x + 3;
Suy ra .
Chọn D.
Câu 14: Thay x = 1 và y = -1 vào các đáp án ta được:
Đáp án A: - 1 – 3.(-1) – 1 < 0 ⇔ 1 < 0 (vô lí).
Đáp án B: - 1 – (-1) < 0 ⇔ 0 < 0 (vô lí).
Đáp án C: 1 + 4.( - 1) < 1 ⇔ - 3 < 1 (luôn đúng).
Đáp án D. 1 + (-1) – 2 > 0 ⇔ - 2 > 0 (vô lí).
Chọn C
Câu 15: Đường thẳng 2x + 3y – 2 = 0 có VTPT là .
Đường thẳng đi qua A(2;1) song song với đường thẳng 2x + 3y – 2 = 0 nên nhận làm VTPT có phương trình: 2(x – 2) + 3.(y – 1) = 0
⇔ 2x + 3y – 7 = 0 .
Chọn C.
Câu 16:
Ta có: - x2 + 2x = 0
Áp dụng định lý dấu của tam thức bậc hai, ta có:
- x2 + 3x > 0 khi 0 < x < 2.
Tam thức nhận giá trị dương khi chỉ khi: 0 < x < 2.
Chọn C.
Câu 17:
Ta có 2x – 2 > 0 ⇔ x > 1.
Vậy với thì f(x) nhận giá trị dương.
Chọn C
Câu 18: Đường thẳng có véctơ chỉ phương là (1;4).
Chọn D.
Câu 19: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP =(3;–4) là:
Chọn B
Câu 20: Tọa độ trung điểm M của AB là: M(2; -1)
Ta có:
Phương trình tổng quát đường trung trực của đoạn thẳng AB đi qua M(2;-1) và nhận là VTPT, ta được:
x – 2 + 3(y + 1) = 0
⇔ x + 3y + 1 = 0.
Chọn A
II. PHẦN TỰ LUẬN (6 điểm)
|
Câu |
Nội dung |
Thang điểm |
|
|
21 3.0 điểm |
a. 1.0 điểm |
Giải bất phương trình * * Lập bảng xét dấu đúng * Kết luận: |
0.25 0.25
0.25 0.25 |
|
b. 1.0 điểm |
Giải bất phương trình * Ta có: * Lập bảng xét dấu đúng * Kết luận: |
0.25 0.25 0.25 0.25 |
|
|
|
c. 1.0 điểm
|
Giải bất phương trình * * Lập bảng xét dấu đúng * Kết luận: |
0.5
0.25 0.25 |
|
22 1.0 điểm |
a. 0.75điểm |
Cho phương trình : , với m là tham số. Tìm tất cả các giá trị của m để phương trình có hai nghiệm trái dấu *Phương trình có hai nghiệm trái dấu |
0.5
0.5
|
|
23 2.0 điểm |
|
Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm và |
|
|
|
a. |
Viết phương trình đường thẳng AB (0.75 điểm) |
|
|
Có là một vectơ chỉ phương của đường thẳng AB |
0.25 |
||
|
Mà đường thẳng AB đi qua điểm .Vậy đường thẳng AB: |
0.5 |
||
|
b |
Tính khoảng cách từ điểm M đến đường thẳng (0.75 điểm) |
|
|
|
0.5 |
|||
|
0.25 |
|||
|
c |
Viết phương trình đường thẳng d, biết d đi qua điểm A và cắt tia Ox;Oy thứ tự tại M,N sao cho tam giác OMN có diện tích nhỏ nhất. (0.5 điểm) |
|
|
|
Gọi thì và Tam giác OMN vuông ở O nên Đường thẳng d cũng đi qua hai điểm M,N nên Do đường thẳng d đi qua điểm A nên ta có: |
0.25 |
||
|
Áp dụng BĐT giữa trung bình cộng và trung bình nhân (BĐT Côsi) cho 2 số dương ta có , dẫn đến khi và chỉ khi . Vậy tam giác có diện tích nhỏ nhất là 4. Khi đó |
0.25 |
||
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
