Chuyên đề Toán 10 Bài 6 (Kết nối tri thức): Hypebol - Kết nối tri thức

Giải bài tập Chuyên đề Toán 10 Bài 6: Hypebol

Giải bài tập trang 47, 48 Chuyên đề Toán 10 Bài 6

HĐ1 trang 47 Chuyên đề Toán 10:

Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$.

a) Hãy giải thích vì sao nếu điểm M(x₀; y₀) thuộc hypebol thì các điểm có toạ độ (x₀; –y₀), (–x₀; y₀), (–x₀; –y₀) cũng thuộc hypebol (H.3.12).

b) Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?

c) Với điểm M(x₀; y₀) thuộc hypebol, hãy so sánh |x₀| với a.

Lời giải:

a) Nếu điểm M(x₀; y₀) thuộc hypebol thì ta có: $\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1.$

Ta có: $\frac{x_0^2}{a^2}-\frac{{\left(-y_0\right)}^2}{b^2}=\frac{{\left(-x_0\right)}^2}{a^2}-\frac{y_0^2}{b^2}$$=\frac{{\left(-x_0\right)}^2}{a^2}-\frac{{\left(-y_0\right)}^2}{b^2}$$=\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1$ nên các điểm có toạ độ (x₀; –y₀), (–x₀; y₀), (–x₀; –y₀) cũng thuộc elip.

b)

+) Gọi A là giao điểm của hypebol với trục hoành.

Vì A thuộc trục Ox nên toạ độ của A có dạng (x_A; 0)

Mà A thuộc hypebol nên

$$\begin{gathered} \frac{x_{{}_A}^2}{a^2}-\frac{0^2}{b^2}=1 \\ \Rightarrow x_A^2=a^2\Rightarrow \left[\begin{array}{l}{x}_A=a\\ x_A=-a\end{array}\right.. \end{gathered}$$

Do đó hypebol cắt trục Ox tại hai điểm A₁(–a; 0) và A₂(a; 0).

+) Giả sử hypebol cắt trục tung tại B.

Vì B thuộc trục Oy nên toạ độ của B có dạng (0; y_B).

Mà B thuộc hypebol nên $\frac{0^2}{a^2}-\frac{y_{{}_B}^2}{b^2}=1\Rightarrow -\frac{y_{{}_B}^2}{b^2}=1$ (vô lí).

Vậy hypebol không cắt trục tung.

c) M(x₀; y₀) thuộc hypebol nên ta có: $\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1.$

Vì $\frac{y_0^2}{b^2}\ge 0$ nên $\frac{x_0^2}{a^2}\le 1\Rightarrow x_0^2\le a^2$$\Rightarrow \left|x_0\right|\le a.$

Luyện tập 1 trang 48 Chuyên đề Toán 10: Cho hypebol $\frac{x^2}{64}-\frac{y^2}{36}=1$.

a) Tìm tiêu cự và độ dài các trục.

b) Tìm các đỉnh và các đường tiệm cận.

Lời giải:

a) Có a² = 64, b² = 36

$\Rightarrow \left\{\begin{array}{l}a=8,b=6\\ c=\sqrt{a^2+b^2}=\sqrt{64+36}=10\end{array}\right..$

Do đó, tiêu cự của hypebol là 2c = 20, độ dài trục thực là 2a = 16, độ dài trục ảo là 2b = 12.

b) Các đỉnh của hypebol là A₁(–8; 0), A₂(8; 0).

Hai đường tiệm cận của hypebol là $y=-\frac{b}{a}x=-\frac{6}{8}x=-\frac{3}{4}x$ và $y=\frac{b}{a}x=\frac{6}{8}x=\frac{3}{4}x.$ 

Giải bài tập trang 49, 50 Chuyên đề Toán 10 Bài 6

HĐ2 trang 49 Chuyên đề Toán 10:

Cho điểm M(x₀; y₀) thuộc hypebol có hai tiêu điểm F₁(–c; 0), F₂(c; 0), độ dài trục thực bằng 2a.

a) Tính MF₁² – MF₂².

b) Giả sử M(x₀; y₀) thuộc nhánh chứa đỉnh A₂(a; 0), tức là, MF₁ – MF₂ = 2a. Tính MF₁ + MF₂, MF₁, MF₂.

c) Giả sử M(x₀; y₀) thuộc nhánh chứa đỉnh A₁(–a; 0), tức là, MF₂ – MF₁ = 2a. Tính MF₁ + MF₂, MF₁, MF₂.

Lời giải:

a) MF₁² – MF₂² = (x² + 2cx + c² + y²) – (x² – 2cx + c² + y²) = 4cx.

b) Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)2a = 4cx

$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = $\frac{2cx}{a}$x. Khi đó:

(MF₁ + MF₂) + (MF₁ – MF₂) = $\frac{2c}{a}x$ + 2a $\Rightarrow$ 2MF₁ = $\frac{2c}{a}x$ + 2a

$\Rightarrow$ MF₁ = a + $\frac{c}{a}$x $=\left|a+\frac{c}{a}x\right|.$

(MF₁ + MF₂) – (MF₁ – MF₂) = $\frac{2c}{a}x$ – 2a $\Rightarrow$ 2MF₂ = $\frac{2c}{a}x$ – 2a

$\Rightarrow$ MF₂ = $\frac{c}{a}$x – a $=\left|a-\frac{c}{a}x\right|.$

c) Ta có: MF₁² – MF₂² = 4cx $\Rightarrow$ (MF₁ + MF₂)(MF₁ – MF₂) = 4cx $\Rightarrow$ (MF₁ + MF₂)(–2a) = 4cx

$\Rightarrow$ MF₁ + MF₂ = $\frac{4cx}{2a}$ = –$\frac{2cx}{a}$x. Khi đó:

(MF₁ + MF₂) + (MF₁ – MF₂) = –$\frac{2c}{a}x$ + (–2a) $\Rightarrow$ 2MF₁ = –$\frac{2c}{a}x$ – 2a

$\Rightarrow$ MF₁ =$-\left(\frac{c}{a}x+a\right)$ $=\left|a+\frac{c}{a}x\right|.$

(MF₁ + MF₂) – (MF₁ – MF₂) = –$\frac{2c}{a}x$ – (–2a) $\Rightarrow$ 2MF₂ = –$\frac{2c}{a}x$ + 2a

$\Rightarrow$ MF₂ =  a –$\frac{c}{a}$x $=\left|a-\frac{c}{a}x\right|.$

Luyện tập 2 trang 50 Chuyên đề Toán 10:

Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6$\sqrt{3}$ Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.

Lời giải:

Hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6$\sqrt{3}\Rightarrow$ 2a = 6, 2b = 6

$\Rightarrow$ a = 3, b = 3$\sqrt{3}\Rightarrow c=\sqrt{a^2+b^2}$$=\sqrt{3^2+{\left(3\sqrt{3}\right)}^2}=6.$

Theo công thức bán kính qua tiêu ta có:

MF₁ $=\left|a+\frac{c}{a}x\right|$$=\left|3+\frac{6}{3}.9\right|=21.$

MF₂ $=\left|a-\frac{c}{a}x\right|$$=\left|3-\frac{6}{3}.9\right|=15.$

Luyện tập 3 trang 50 Chuyên đề Toán 10:

Cho hypebol $\frac{x^2}{1}-\frac{y^2}{3}=1$ với hai tiêu điểm F₁(–2; 0), F₂(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính tiêu MF₂ nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.

Lời giải:

Có a² = 1, b² = 3 $\Rightarrow a=1,b=\sqrt{3}$$\Rightarrow c=\sqrt{a^2+b^2}=2.$

Gọi (x; y) là toạ độ của M.

Theo công thức bán kính qua tiêu ta có: MF₂ $=\left|a-\frac{c}{a}x\right|$$=\left|1-\frac{2}{1}.x\right|=\left|1-2x\right|.$

Nếu M thuộc nhánh bên trái thì x ≤ –a = –1. Khi đó 1 – 2x ≥ 1 – 2(–1) = 3.

Suy ra MF₂ = |1 – 2x| ≥ 3.

Nếu M thuộc nhánh bên phải thì x ≥ a = 1. Khi đó 1 – 2x ≤ 1 – 2.1 = –1.

Suy ra MF₂ = |1 – 2x| ≥ 1.

Vậy MF₂ nhỏ nhất bằng 1 khi x = 1.

Khi đó MF₁ $=\left|a+\frac{c}{a}x\right|=\left|1+\frac{2}{1}.1\right|=3.$

HĐ3 trang 50 Chuyên đề Toán 10:

Cho hypebol có phương trình chính tắc $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với các tiêu điểm F₁(–c; 0), F₂(c; 0). Xét các đường thẳng ${\Delta }_1:x=-\frac{a^2}{c}$ và ${\Delta }_2:x=\frac{a^2}{c}$ (H.3.14). Với điểm M(x; y) thuộc hypebol, tính các tỉ số $\frac{M{F}_1}{d\left(M,{\Delta }_1\right)}$ và $\frac{M{F}_2}{d\left(M,{\Delta }_2\right)}$ theo a và c.

Lời giải:

+) Viết lại phương trình đường thẳng Δ₁ ở dạng: $x+0y+\frac{a^2}{c}=0.$ Với mỗi điểm M(x; y) thuộc elip, ta có: $d\left(M,{\Delta }_1\right)=\frac{\left|x+0y+\frac{a^2}{c}\right|}{\sqrt{1^2+0^2}}$$=\left|x+\frac{a^2}{c}\right|.$

suy ra $\frac{M{F}_1}{d\left(M,{\Delta }_1\right)}=\frac{\left|a+\frac{c}{a}x\right|}{\left|x+\frac{a^2}{c}\right|}$$=\frac{\left|\frac{a^2+cx}{a}\right|}{\left|\frac{xc+a^2}{c}\right|}=\left|\frac{c}{a}\right|=\frac{c}{a}.$

+) Viết lại phương trình đường thẳng Δ₂ ở dạng: $x+0y-\frac{a^2}{c}=0.$ Với mỗi điểm M(x; y) thuộc elip, ta có: $d\left(M,{\Delta }_2\right)=\frac{\left|x+0y-\frac{a^2}{c}\right|}{\sqrt{1^2+0^2}}$$=\left|x-\frac{a^2}{c}\right|.$

suy ra $\frac{M{F}_2}{d\left(M,{\Delta }_2\right)}=\frac{\left|a-\frac{c}{a}x\right|}{\left|x-\frac{a^2}{c}\right|}$$=\frac{\left|\frac{a^2-cx}{a}\right|}{\left|\frac{xc-a^2}{c}\right|}=\left|\frac{c}{a}\right|=\frac{c}{a}.$

Giải bài tập trang 52 Chuyên đề Toán 10 Bài 6

Luyện tập 4 trang 52 Chuyên đề Toán 10: Trong mặt phẳng toạ độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai e = 2 và một đường chuẩn là x = 8. Lập phương trình chính tắc của (H).

Lời giải:

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có tâm sai 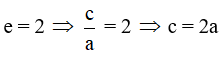(1).

+) Hypebol có một đường chuẩn là

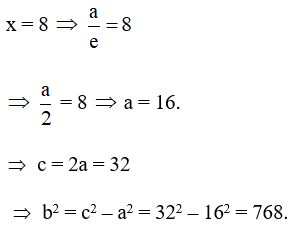
Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{256}-\frac{y^2}{768}=1.$

Vận dụng trang 52 Chuyên đề Toán 10:

Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt Trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt Trời là 3.10⁸ km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15).

Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng toạ độ ứng với 10⁸ km trên thực tế.

Lời giải:

Chọn hệ trục toạ độ sao cho tâm Mặt Trời trùng với tiêu điểm F₁ của hypebol.

Gọi phương trình chính tắc của hypebol là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Theo đề bài, ta có:

– Khoảng cách gần nhất từ sao chổi này đến tâm Mặt Trời là 3.10⁸ km $\Rightarrow$ c – a = 3.

– Tâm sai của quỹ đạo hypebol là 3,6

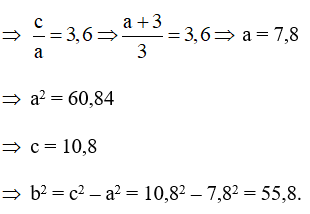
Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{60,84}-\frac{y^2}{55,8}=1.$

Bài 3.7 trang 52 Chuyên đề Toán 10:

Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc $\frac{x^2}{9}-\frac{y^2}{4}=1$. Xác định toạ độ các đỉnh, độ dài các trục, tâm sai và phương trình các đường chuẩn của hypebol.

Lời giải:

Có a² = 9, b² = 4 $\Rightarrow$ a = 3, b = 2, c = $\sqrt{a^2+b^2}$$=\sqrt{9+4}=\sqrt{13}.$

Toạ độ các đỉnh của hypebol là A₁(–3; 0), A₂(3; 0).

Độ dài trục thực là 2a = 6, độ dài trục ảo là 2b = 4.

Tâm sai e = $\frac{c}{a}=\frac{\sqrt{13}}{3}.$

Phương trình các đường chuẩn của hypebol là: ${\Delta }_1:x=-\frac{a^2}{c}\iff x=-\frac{9}{\sqrt{13}},$ ${\Delta }_2:x=\frac{a^2}{c}\iff x=\frac{9}{\sqrt{13}}.$

Bài 3.8 trang 52 Chuyên đề Toán 10:

Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc $\frac{x^2}{9}-\frac{y^2}{7}=1$. Tính bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 12.

Lời giải:

Có a² = 9, b² = 7 $\Rightarrow a=3,c=\sqrt{a^2+b^2}$$=\sqrt{9+7}=4.$

Độ dài các bán kính qua tiêu của M là:

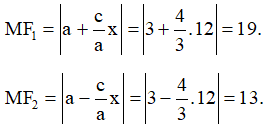
Bài 3.9 trang 52 Chuyên đề Toán 10:

Trong mặt phẳng toạ độ, hypebol (H) có phương trình chính tắc. Lập phương trình chính tắc của (H) trong mỗi trường hợp sau:

a) (H) có nửa trục thực bằng 4, tiêu cự bằng 10;

b) (H) có tiêu cự bằng $2\sqrt{13}$, một đường tiệm cận là $y=\frac{2}{3}x$;

c) (H) có tâm sai $e=\sqrt{5}$, và đi qua điểm $(\sqrt{10};6)$.

Lời giải:

a)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có nửa trục thực bằng 4 $\Rightarrow$ a = 4.

+) Hypebol có tiêu cự bằng 10 $\Rightarrow$ 2c = 10 $\Rightarrow$ c = 5 $\Rightarrow$ b² = c² – a² = 5² – 4² = 9.

Vậy phương trình chính tắc của hypebol đã cho là hay $\frac{x^2}{16}-\frac{y^2}{9}=1.$

b)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có tiêu cự bằng 

+) Hypebol có một đường tiệm cận là $y=\frac{2}{3}x$ $\Rightarrow \frac{b}{a}=\frac{2}{3}$

$\Rightarrow \frac{b}{2}=\frac{a}{3}\Rightarrow \frac{b^2}{4}=\frac{a^2}{9}$$=\frac{b^2+a^2}{4+9}=\frac{c^2}{13}=\frac{{\left(\sqrt{13}\right)}^2}{13}=1$ $\Rightarrow \left\{\begin{array}{l}{b}^2=4\\ a^2=9\end{array}\right..$

Vậy phương trình chính tắc của hypebol đã cho là hay $\frac{x^2}{9}-\frac{y^2}{4}=1.$

c)

Gọi phương trình chính tắc của hypebol đã cho là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

+) Hypebol có tâm sai

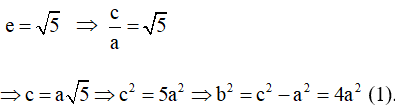
+) Hypebol đi qua điểm $(\sqrt{10};6)$ $\Rightarrow$ $\frac{{\left(\sqrt{10}\right)}^2}{a^2}-\frac{6^2}{b^2}=1$$\Rightarrow \frac{10}{a^2}-\frac{36}{b^2}=1$ (2).

Thế (1) vào (2) ta được:

$$\begin{gathered} \Rightarrow \frac{10}{a^2}-\frac{36}{4a^2}=1 \\ \Rightarrow \frac{10}{a^2}-\frac{9}{a^2}=1 \\ \Rightarrow \frac{1}{a^2}=1\Rightarrow a^2=1 \\ \Rightarrow b^2=4. \end{gathered}$$

Vậy phương trình chính tắc của hypebol đã cho là $\frac{x^2}{1}-\frac{y^2}{4}=1.$

Bài 3.10 trang 52 Chuyên đề Toán 10:

Một hypebol mà độ dài trục thực bằng độ dài trục ảo được gọi là hypebol vuông. Tìm tâm sai và phương trình hai đường tiệm cận của hypebol vuông.

Lời giải:

Giả sử phương trình chính tắc của một hypebol vuông là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Vì độ dài trục thực bằng độ dài trục ảo nên a = b $\Rightarrow c=\sqrt{a^2+b^2}=\sqrt{a^2+a^2}=a\sqrt{2}$

$\Rightarrow$ Tâm sai e = $\frac{c}{a}=\frac{a\sqrt{2}}{a}=\sqrt{2}.$

Phương trình hai đường tiệm cận là: $y=-\frac{b}{a}x\iff y=-x$ và $y=\frac{b}{a}x\iff y=x.$

Bài 3.11 trang 52 Chuyên đề Toán 10:

Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.

Lời giải:

Xét hypebol có phương trình chính tắc là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Hai đường tiệm cận của hypebol là: d₁ : $y=-\frac{b}{a}x$ hay bx + ay = 0 và d₂ : $y=\frac{b}{a}x$ hay bx – ay = 0.

Xét điểm M(x; y) bất kì thuộc hypebol. Ta có:

d(M, d₁) = $\frac{\left|bx+ay\right|}{\sqrt{b^2+a^2}}$, d(M, d₂) = $\frac{\left|bx-ay\right|}{\sqrt{b^2+a^2}}$.

$\iff$ d(M, d₁).d(M, d₂) = $\frac{\left|bx+ay\right|}{\sqrt{b^2+a^2}}.\frac{\left|bx-ay\right|}{\sqrt{b^2+a^2}}$$=\frac{\left|{\left(bx\right)}^2-{\left(ay\right)}^2\right|}{a^2+b^2}$ (*).

Mặt khác, vì M(x; y) thuộc hypebol nên

$$\begin{gathered} \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \\ \Rightarrow \frac{x^2{b}^2-a^2{y}^2}{a^2{b}^2}=1 \end{gathered}$$

$\Rightarrow {\left(bx\right)}^2-{\left(ay\right)}^2=a^2{b}^2$

Thay vào (*) ta được: d(M, d₁).d(M, d₂) = $\frac{\left|a^2{b}^2\right|}{a^2+b^2}=\frac{a^2{b}^2}{a^2+b^2}$ (không đổi).

Vậy tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.

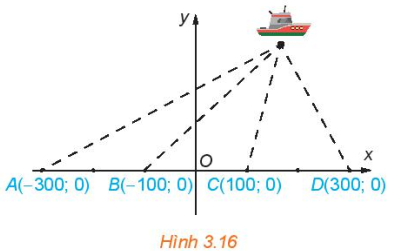
Bài 3.12 trang 52 Chuyên đề Toán 10:

Bốn trạm phát tín hiệu vô tuyến có vị trí A, B, C, D theo thứ tự đó thẳng hàng và cách đều với khoảng cách 200 km (H.3.16). Tại một thời điểm, bốn trạm cùng phát tín hiệu với vận tốc 292000 km/s. Một tàu thuỷ nhận được tín hiệu từ trạm C trước 0,0005 s so với tín hiệu từ trạm B và nhận được tín hiệu từ trạm D sớm 0,001 s so với tín hiệu từ trạm A.

a) Tính hiệu các khoảng cách từ tàu đến các trạm B, C.

b) Tính hiệu các khoảng cách từ tàu đến các trạm A, D.

c) Chọn hệ trục tọa độ Oxy như trong Hình 3.16 (1 đơn vị trên mặt phẳng toạ độ ứng với 100 km trên thực tế). Hãy lập phương trình chính tắc của hai hypebol đi qua vị trí M của tàu. Từ đó, tính toạ độ của M (các số được làm tròn đến hàng đơn vị).

d) Tính các khoảng cách từ tàu đến các trạm B, C (đáp số được làm tròn đến hàng đơn vị, tính theo đơn vị km).

Lời giải:

Gọi vận tốc phát tín hiệu là v (theo đề bài v = 292000 km/s);

t_A, t_B, t_C, t_D lần lượt là thời gian để tàu nhận được tín hiệu từ các trạm A, B, C, D;

M là vị trí của tàu thuỷ.

a) Hiệu các khoảng cách từ tàu đến các trạm B, C là:

MB – MC = v.t_B – v.t_C = v(t_B – t_C) = 292000 . 0,0005 = 146 (km).

b) Hiệu các khoảng cách từ tàu đến các trạm A, D là:

MA – MD = v.t_D – v.t_A = v(t_D – t_A) = 292000 . 0,001 = 292 (km).

c)

+) Gọi phương trình chính tắc của hypebol (H₁) nhận B, C làm tiêu điểm là $\frac{x^2}{a_1^2}-\frac{y^2}{b_1^2}=1$ (a₁ > 0, b₁ > 0).

Vì MB – MC = 146 nên 2a₁ = 146 $\Rightarrow$ a₁ = 73$\Rightarrow a_1^2$ = 5329.

Ta thấy B(–100; 0) và C(100; 0) là hai tiêu điểm của hypebol nên c₁ = 100

 $\Rightarrow b_1^2=c_1^2-a_1^2$ = 100² – 73² = 4671.

Vậy phương trình chính tắc của hypebol (H₁) là $\frac{x^2}{5329}-\frac{y^2}{4671}=1.$

+) Gọi phương trình chính tắc của hypebol (H₂) nhận A, D làm tiêu điểm là $\frac{x^2}{a_2^2}-\frac{y^2}{b_2^2}=1$ (a₂ > 0, b₂ > 0).

Vì MA – MD = 29,2 nên 2a₂ = 292 $\Rightarrow$ a₂ = 146

Ta thấy A(–300; 0) và D(300; 0) là hai tiêu điểm của hypebol nên c₂ = 300

 $\Rightarrow b_2^2=c_2^2-a_2^2$ = 300² – 146² = 68684.

Vậy phương trình chính tắc của hypebol (H₂) là $\frac{x^2}{21316}-\frac{y^2}{68684}=1.$

Gọi toạ độ của M là (x; y). Vì M thuộc cả (H₁) và (H₂) nên ta có:

$\left\{\begin{array}{l}\frac{x^2}{5329}-\frac{y^2}{4671}=1\\ \frac{x^2}{21316}-\frac{y^2}{68684}=1\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}{x}^2=\frac{341125277}{12500}\\ y^2=\frac{240617223}{12500}\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}x\approx 165\\ y\approx 139\end{array}\right.$ (vì theo hình vẽ x, y > 0)

d) MB = $\sqrt{{\left[165-\left(-100\right)\right]}^2+{\left(139-0\right)}^2}$≈ 299 (km);

MC = $\sqrt{{\left(165-100\right)}^2+{\left(139-0\right)}^2}$≈ 153 (km).

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài tập cuối chuyên đề 2

Bài 5: Elip

Bài 7: Parabol

Bài 8: Sự thống nhất giữa ba đường conic

Bài tập cuối chuyên đề 3