Nội dung bài viết

    Xem thêm

    Cho tam giác ABC có góc A = góc B + góc C. Hai đường phân giác của góc B và C cắt nhau tại O

    Lời giải Bài 1 trang 65 SBT Toán 7 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 348 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 Chân trời sáng tạo Bài tập cuối chương 8

    Bài 1 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC có A^=B^+C^. Hai đường phân giác của góc B và C cắt nhau tại O.

    a) Tính số đo góc A

    b) Tính số đo góc BOC.

    Lời giải

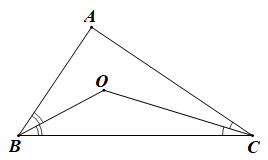
    Sách bài tập Toán 7 (Kết nối tri thức) Bài tập cuối chương 8 (ảnh 1)

    a) Trong ∆CAB ta có: A^+ABC^+ACB^=180° (tổng ba góc trong một tam giác).

    Mà A^=ABC^+ACB^ (giả thiết).

    Suy ra A^=ABC^+ACB^=180°2=90°.

    Vậy A^=90°.

    b) Vì BO là phân giác của góc ABC nên ABO^=CBO^=ABC^2

    Vì CO là phân giác của góc ACB nên ACO^=BCO^=ACB^2

    Trong ∆COB ta có: BOC^+OBC^+OCB^=180° (tổng ba góc trong một tam giác).

    Mà CBO^=ABC^2 , BCO^=ACB^2, ABC^+ACB^=90°.

    Suy ra BOC^=180°−ABC^+ACB^2=180°−90°2=135°

    Vậy BOC^=135°.

    Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

    Bài 1 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC có A^=B^+C^. Hai đường phân giác của góc B và C cắt nhau tại O...

    Bài 2 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC có M là điểm đồng quy của ba đường phân giác. Qua M vẽ đường thẳng song song với BC và cắt AB, AC lần lượt tại N và P...

    Bài 3 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC có M là giao điểm của hai phân giác của góc B và góc C. Cho biết BMC^=132°. Tính số đo các góc MAB^ và MAC^...

    Bài 4 trang 65 SBT Toán 7 Tập 2: Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA...

    Bài 5 trang 65 SBT Toán 7 Tập 2: Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho: MA + MB + MC + MD nhỏ nhất...

    Bài 6 trang 65 SBT Toán 7 Tập 2: a) Chứng minh trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh...

    Bài 7 trang 66 SBT Toán 7 Tập 2: Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng BIH^=CID^. ..

    Bài 8 trang 66 SBT Toán 7 Tập 2:  Cho tam giác ABC cân tại A và cho A^=124°. Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK...

    Bài 9 trang 66 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC...

    Bài 10 trang 66 SBT Toán 7 Tập 2: Cho tam giác nhọn ABC. Hãy nêu cách tìm các điểm sau đây bên trong tam giác ABC. a) Điểm M cách đều ba đỉnh của tam giác ABC...

    Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

    Bài 8: Tính chất ba đường cao của tam giác

    Bài 9: Tính chất ba đường phân giác của tam giác

    Bài 1: Làm quen với yếu tố ngẫu nhiên

    Bài 2: Làm quen với xác xuất của biến cố ngẫu nhiên

    Bài tập cuối chương 9

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 348 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: