Câu hỏi:
07/12/2024 183Tính giá trị của biểu thức A = sin6x + cos6x + 3sin2x.cos2x.
A. -1
B. 1
C. 3
D. - 2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là B.
Lời giải
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1
*Phương pháp giải:
Để rút gọn biểu thức và chứng minh đẳng thức lượng giác ta sử dụng các công thức lượng giác để biến đổi biểu thức và đẳng thức lượng giác nhằm triệt tiêu các giá trị lượng giác không đặc biệt.
*Lý thuyết:
* Các công thức thường sử dụng:
* Các hệ thức lượng giác cơ bản:
√ sin2 α + cos2 α = 1;
√( , k ∈ ℤ);
√ (α ≠ kπ , k ∈ ℤ);
√ tanα⋅cotα=1( , k ∈ ℤ).
* Giá trị lượng giác của các góc liên quan đặc biệt:
√ Hai góc đối nhau (α và – α): cos (– α) = cos α; sin (– α) = – sin α;
tan (– α) = – tan α; cot (– α) = – cot α.
√ Hai góc bù nhau (α và π – α): sin (π – α) = sin α; cos (π – α) = – cos α;
tan (π – α) = – tan α; cot (π – α) = – cot α.
√ Hai góc phụ nhau (α và π2– α): sin = cos α; cos = sin α;
tan = cot α; cot = tan α.
√ Hai góc hơn kém nhau π (α và π + α): sin (π + α) = – sin α; cos (π + α) = – cos α;
tan (π + α) = tan α; cot (π + α) = cot α
Xem thêm
Công thức lượng giác (2024) và cách giải bài tập chi tiết nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 14:
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
Câu 15:
Cho tam giác ABC và các mệnh đề :
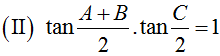
(III): cos(A + B - C) – cos 2C=0
Mệnh đề đúng là :

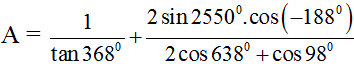 bằng :
bằng :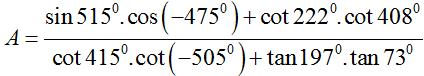
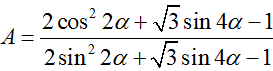
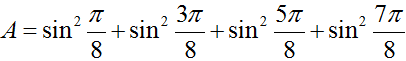 bằng
bằng