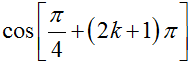Câu hỏi:
17/06/2026 415Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b =
Đáp án chính xác
Trả lời:
Giải bởi Vietjack
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho A; B; C là ba góc của một tam giác. Hãy chỉ ra hệ thức sai
Xem đáp án »
17/06/2026
15,929
. Tính 
Câu 5:
Cho A ; B; C là ba góc của một tam giác . Hãy chỉ ra hệ thức sai
Xem đáp án »
17/06/2026
2,234
Câu 8:
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
Xem đáp án »
17/06/2026
1,776
Câu 10:
Cho A; B: C là ba góc của một tam giác không vuông. Hệ thức nào sau đây sai?
Xem đáp án »
17/06/2026
1,533
Câu 13:
Cho x và y là các góc nhọn, cotx = 3/4, cot y = 1/7. Tổng 2 góc đó là:
Xem đáp án »
17/06/2026
652
bằng:
