Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$?

Đáp án đúng là: B

*Phương pháp giải:

Sử dụng định nghĩa hai vecto bằng nhau.

- Độ dài đoạn thẳng $AB$ gọi là độ dài véc tơ $\overrightarrow{AB}$, kí hiệu $\left|\overrightarrow{AB}\right|$.

Vậy $\left|\overrightarrow{AB}\right|=AB$.

- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.

*Lời giải:

Ta có:

$•\overrightarrow{AB}=\overrightarrow{CD}\Rightarrow \left\{\begin{array}{l}AB//CD\\ AB=CD\end{array}\right.$

$\Rightarrow$ ABDC là hình bình hành.

 Mặt khác, ABDC là hình bình hành 

$\Rightarrow \left\{\begin{array}{l}AB//CD\\ AB=CD\end{array}\right.\Rightarrow \overrightarrow{AB}=\overrightarrow{CD}$

Do đó, điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$ là ABDC là hình bình hành.

* Một số lý thuyết liên quan:

Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.

Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu : $\overrightarrow{AB}$

Vectơ còn được kí hiệu là: $\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},\mathrm{...}$

Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là $\overrightarrow{0}$

 

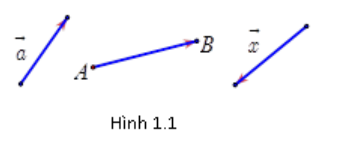
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ

- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương

- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.

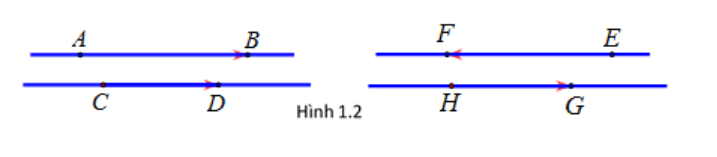
Ví dụ: Ở hình vẽ trên trên (hình 2) thì hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng hướng còn $\overrightarrow{EF}$ và $\overrightarrow{HG}$ ngược hướng.

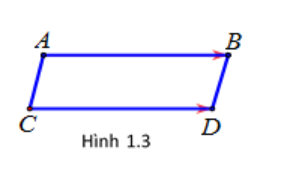
Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Các định nghĩa vecto có đáp án

Trắc nghiệm Toán 10 Bài 7. Khái niệm vectơ có đáp án

80 câu trắc nghiệm Vectơ cơ bản