Câu hỏi:
22/11/2024 7,423
Cho →AB≠→0 và một điểm C, có bao nhiêu điểm D thỏa mãn →AB=→CD.
A. 1.
B. 2.
C. 0.
D. Vô số.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
* Lời giải:
AB=CD⇔{AB//CD AB=CD
?? và ?? cùng hướng⇔{??//?? ??=?D
Nên có duy nhất một điểm D để AB=CD
* Phương pháp giải:
Sử dụng định nghĩa hai vecto bằng nhau.
*Một số lý thuyết và dạng bài tập về vectơ:
Hai vectơ →AB, →CD bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: →AB=→CD.
Nhận xét:
– Hai vectơ →a và →b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu →a = →b.
– Khi cho trước vectơ →a và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho →OA=→a.
Tổng của hai vectơ
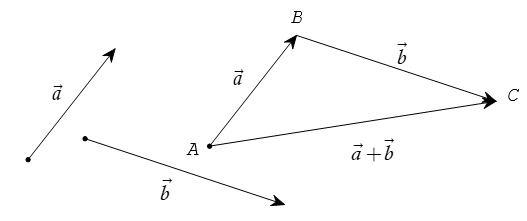
Định nghĩa. Cho hai vectơ 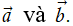 Lấy một điểm A tùy ý, vẽ
Lấy một điểm A tùy ý, vẽ 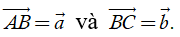 Vectơ
Vectơ 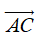 được gọi là tổng của hai vectơ
được gọi là tổng của hai vectơ 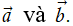 Ta kí hiệu tổng của hai vectơ
Ta kí hiệu tổng của hai vectơ 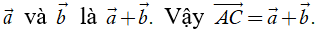
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
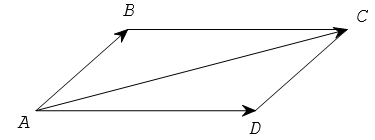
Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì 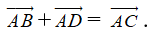
Tính chất của phép cộng các vectơ
Với ba vectơ 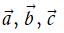 tùy ý ta có
tùy ý ta có
• 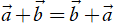 (tính chất giao hoán);
(tính chất giao hoán);
• 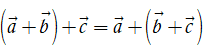 (tính chất kết hợp);
(tính chất kết hợp);
• 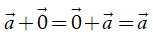 (tính chất của vectơ – không).
(tính chất của vectơ – không).
Hiệu của hai vectơ
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của 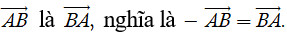
Đặc biệt, vectơ đối của vectơ 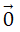 là vectơ
là vectơ 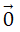 .
.
Định nghĩa hiệu của hai vectơ
Định nghĩa. Cho hai vectơ 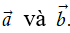 Ta gọi hiệu của hai vectơ
Ta gọi hiệu của hai vectơ 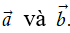 là vectơ
là vectơ 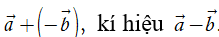
Như vậy 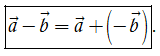
Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có 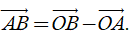
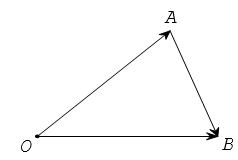
Chú ý
1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.
2) Với ba điểm tùy ý A, B, C ta luôn có
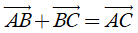 (quy tắc ba điểm);
(quy tắc ba điểm);
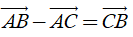 (quy tắc trừ).
(quy tắc trừ).
Áp dụng
a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi 
b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi 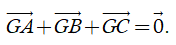
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khái niệm vectơ – Toán 10 Cánh diều
* Lời giải:
AB=CD⇔{AB//CD AB=CD
?? và ?? cùng hướng⇔{??//?? ??=?D
Nên có duy nhất một điểm D để AB=CD
* Phương pháp giải:
Sử dụng định nghĩa hai vecto bằng nhau.
*Một số lý thuyết và dạng bài tập về vectơ:
Hai vectơ →AB, →CD bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: →AB=→CD.
Nhận xét:
– Hai vectơ →a và →b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu →a = →b.
– Khi cho trước vectơ →a và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho →OA=→a.
Tổng của hai vectơ
Định nghĩa. Cho hai vectơ 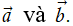
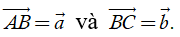
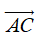
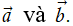
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì
Tính chất của phép cộng các vectơ
Với ba vectơ 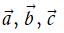
• 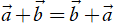
• 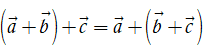
• 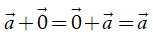
Hiệu của hai vectơ
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của
Đặc biệt, vectơ đối của vectơ 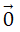
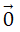
Định nghĩa hiệu của hai vectơ
Định nghĩa. Cho hai vectơ 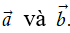
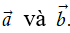
Như vậy
Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có
Chú ý
1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.
2) Với ba điểm tùy ý A, B, C ta luôn có
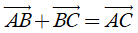
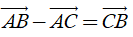
Áp dụng
a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi
b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khái niệm vectơ – Toán 10 Cánh diềuCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của lục giác.
Câu 2:
Cho hình bình hành ABCD. Các vectơ là vectơ đối của vectơ →AD là
Câu 5:
Cho hai điểm phân biệt A, B. Số vectơ ( khác →0) có điểm đầu và điểm cuối lấy từ các điểm A, B là:
Câu 6:
Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm AB, BC, AD. Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:
Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm AB, BC, AD. Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:
Câu 7:
Cho hình thang ABCD có hai đáy là AB và CD với AB=2CD. Từ C vẽ →CI=→DA. Khẳng định nào sau đây là đúng nhất?
Câu 8:
Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để →AB=→CD?
Câu 9:
Cho khẳng định sau
(1). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì →AB=→CD.
(2). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì →AD=→CB.
(3). Nếu →AB=→CD thì 4 điểm A, B, C, D là 4 đỉnh của hình bình hành.
(4). Nếu →AD=→CB thì 4 điểm A, B, C, D theo thứ tự đó là 4 đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai?
Cho khẳng định sau
(1). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì →AB=→CD.
(2). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì →AD=→CB.
(3). Nếu →AB=→CD thì 4 điểm A, B, C, D là 4 đỉnh của hình bình hành.
(4). Nếu →AD=→CB thì 4 điểm A, B, C, D theo thứ tự đó là 4 đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai?


