Lý thuyết Tin học 12 Bài 2 (Cánh diều): Thực hành về mô phỏng

Lý thuyết Tin học 12 Bài 2: Thực hành về mô phỏng

Nhiệm vụ 1. Thể hiện trực quan một số định lí hình học bằng phần mềm GeoGebra

Yêu cầu:

Sử dụng phần mềm GeoGebra để vẽ hình và kiểm chứng các định lý hình học sau:

a) Ba đường phân giác của ba góc trong một tam giác cùng đi qua một điểm.

b) Giao điểm của các đường phân giác trong một tam giác là tâm đường tròn nội tiếp tam giác đó.

Hướng dẫn thực hiện:

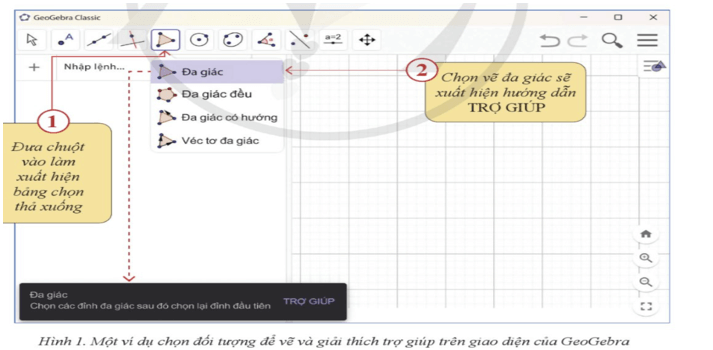
Mở phần mềm GeoGebra: - Nháy đúp chuột vào biểu tượng của phần mềm để mở giao diện làm việc.

a) Kiểm chứng định lý: Ba đường phân giác của ba góc trong một tam giác cùng đi qua một điểm.

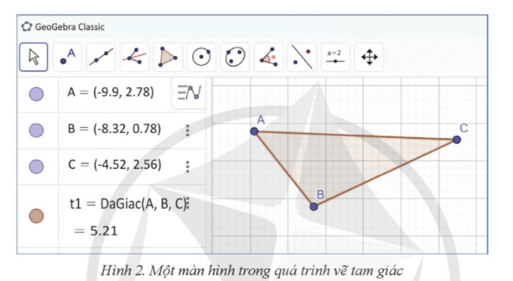
Bước 1: Vẽ tam giác:

- Chọn biểu tượng vẽ Đa giác trên thanh công cụ (biểu tượng hình đa giác).

- Chọn ba điểm trên giao diện để tạo thành tam giác (ví dụ: A, B, C).

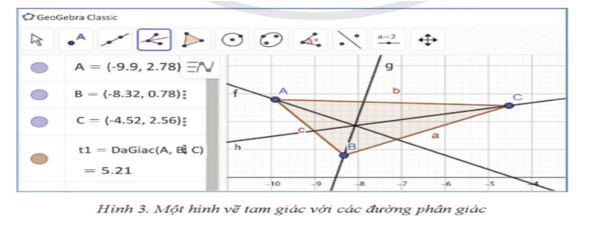
Bước 2: Vẽ các đường phân giác:

- Chọn biểu tượng vẽ Đường phân giác trên thanh công cụ (biểu tượng đường phân giác).

- Nhấp lần lượt các điểm của góc cần vẽ đường phân giác (Ví dụ: chọn B, A, C để vẽ đường phân giác của góc A).

- Lặp lại để vẽ hai đường phân giác còn lại.

­ - Quan sát để xác nhận rằng ba đường phân giác cắt nhau tại một điểm.

Kết quả mong đợi: - Ba đường phân giác của tam giác cắt nhau tại một điểm duy nhất, chứng minh định lý rằng chúng cùng đi qua một điểm.

Bước 3. Thay đổi vị trí của các đỉnh tam giác và quan sát các đường phân giác vẫn luôn đi qua một điểm dù tam giác có biến dạng.

Một số lưu ý:

- Để hoàn tác thay đổi, chọn biểu tượng mũi tên ở góc trên bên phải màn hình.

- Để chọn đối tượng, nhấp vào tên đối tượng đó.

- Để xóa đối tượng, nhấp chuột phải vào đối tượng và chọn "Xoá".

- Để lưu hoặc tạo file mới, chọn biểu tượng "tệp" (=) ở góc trên bên phải màn hình.

b) Kiểm chứng định lý: Giao điểm của các đường phân giác trong một tam giác là tâm đường tròn nội tiếp tam giác đó.

Bước 1:

- Vẽ tam giác ABC và hai đường phân giác của nó.

- Xác định giao điểm của hai đường phân giác bằng cách chọn công cụ "Giao điểm của 2 đối tượng" và nhấp vào giao điểm để đặt tên điểm mới là D.

Bước 2:

- Vẽ đường thẳng đi qua điểm D và vuông góc với cạnh AC:

- Chọn biểu tượng "Đường vuông góc", sau đó chọn điểm D và đoạn AC.

- Xác định giao điểm E của đường thẳng vừa vẽ với cạnh AC bằng cách sử dụng công cụ tương tự như Bước 1.

Bước 3:

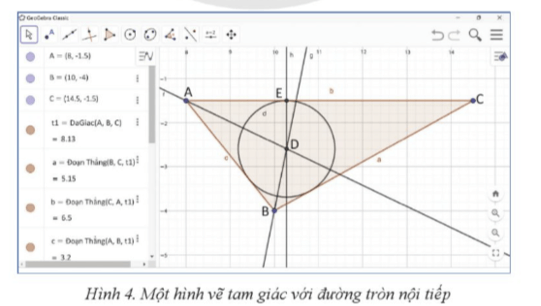
- Vẽ đường tròn có tâm là D và đi qua điểm E:

- Chọn biểu tượng "Đường tròn khi biết tâm và 1 điểm trên đường tròn", chọn tâm D và điểm E.

- Quan sát để thấy đường tròn này chính là đường tròn nội tiếp tam giác ABC.

Bước 4. Thay đổi vị trí của các đỉnh tam giác và quan sát để thấy mỗi khi tam giác biến dạng thành tam giác khác thì giao điểm của các đường phân giác trong tam giác vẫn là tâm đường tròn nội tiếp của tam giác đó.

Nhiệm vụ 2. Tìm một quy luật hình học bằng mô phỏng của GeoGebra

Yêu cầu:

Vẽ nửa đường tròn tâm O đường kính AB. Lấy C, D là hai điểm trên nửa đường tròn sao cho OC vuông góc với OD (C thuộc cung AD). Các tia AC và BD cắt nhau ở P. Cho C thay đổi vị trí (di chuyển) trên nửa đường tròn, quan sát thay đổi vị trí của điểm P

Hướng dẫn thực hiện:

Bước 1. Vẽ nửa đường tròn tâm O đường kính AB.

– Trên thanh công cụ , chọn Hình bán nguyệt qua 2 điểm, rồi thao tác chọn hai điểm A và B.

– Lấy trung điểm của đoạn thẳng AB, GeoGebra tự động đặt tên cho điểm này là C. Nháy chuột phải vào tên điểm C và đổi tên điểm này thành O.

Bước 2. Vẽ OC và OD vuông góc với nhau, với C và D là hai điểm trên cung AB, C nằm phía bên trái D.

– Vẽ đoạn thẳng OC: lấy một điểm C trên nửa bên trái cung tròn AB, vẽ đoạn thẳng OC.

Vẽ đường thẳng đi qua điểm O và vuông góc với OC: chọn biểu tượng X, chọn Đường vuông góc, chọn điểm O và chọn đoạn thẳng OC để xuất hiện đường thẳng cần vẽ. – Lấy giao điểm D của cung tròn AB với đường thẳng vừa vẽ được (đi qua O và vuông góc với OC).

Bước 3. Vẽ tia AC và tia BD.

– Vẽ tia AC: chọn biểu tượng ~, chọn Tia đi qua 2 điểm, rồi lần lượt chọn điểm A và điểm C.

– Tương tự, vẽ tia BD.

Bước 4. Lấy P là giao điểm của tia AC và tỉa BD.

Bước 5. Đặt chế độ lưu vết di chuyển của P: nháy chuột phải vào tên P, trong bảng chọn vừa xuất hiện nháy chuột chọn Hiển thị dấu vết khi di chuyển.

Bước 6. Cho điểm C di chuyển trên nửa đường tròn đường kính AB và quan sát vết mà điểm P di chuyển tạo ra. Trong Hình 5, hai cung tròn có màu đỏ cho thấy vị trí điểm P thay đổi như thế nào khi cho điểm C di chuyển trên cung AB.