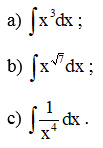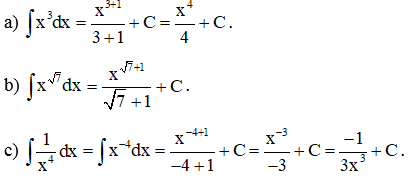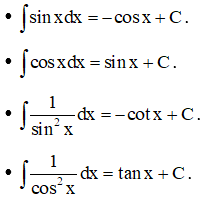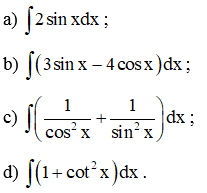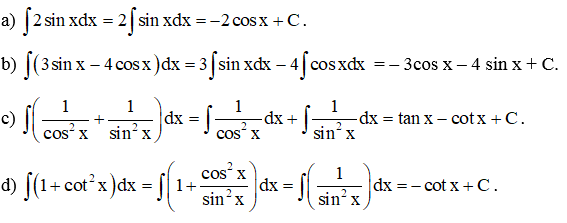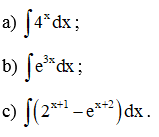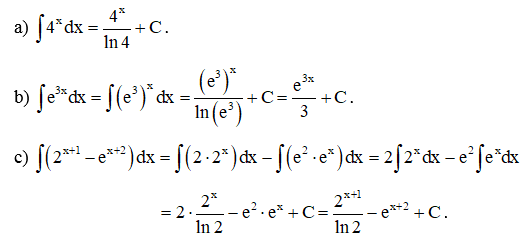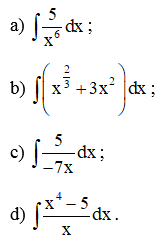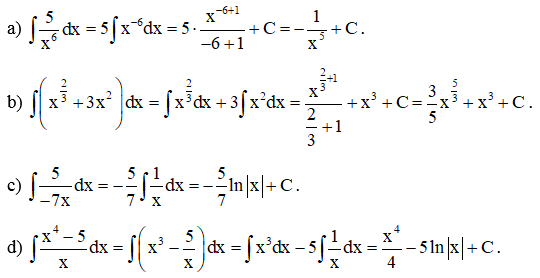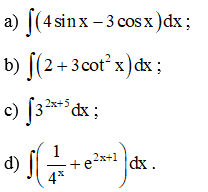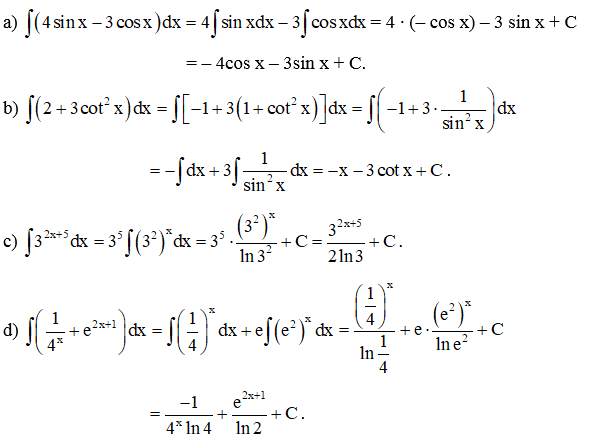Lý thuyết Nguyên hàm của một số hàm số sơ cấp – Toán lớp 12 Cánh diều
Với lý thuyết Toán lớp 12 Bài 2: Nguyên hàm của một số hàm số sơ cấp chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 12.
Lý thuyết Toán 12 Bài 2: Nguyên hàm của một số hàm số sơ cấp- Cánh diều
A. Lý thuyết Nguyên hàm của một số hàm số sơ cấp
1. Nguyên hàm của hàm số luỹ thừa
1.1. Hàm số luỹ thừa
● Cho số thực α. Hàm số y = xα được gọi là hàm số luỹ thừa.
Ví dụ 1. Các hàm số y = x3; y = x– 2; y = ; y = là những hàm số lũy thừa.
● Tập xác định của hàm số lũy thừa y = xα tùy thuộc vào giá trị của α. Cụ thể như sau:
+ Với α nguyên dương, tập xác định là ℝ;
+ Với α nguyên âm hoặc bằng 0, tập xác định là ℝ \ {0};
+ Với α không nguyên, tập xác định là (0; + ∞).
● Định lí: Hàm số lũy thừa y = xα (α ∈ ℝ) có đạo hàm với mọi x > 0 và (xα)' = αxα – 1.
1.2. Nguyên hàm của hàm số luỹ thừa
Với α ≠ – 1, ta có: .
Ví dụ 2. Tìm:
Hướng dẫn giải
2. Nguyên hàm của hàm số f(x) =
Ta có: .
Ví dụ 3. Tìm:
a) ;
b)
Hướng dẫn giải
a) .
b) .
3. Nguyên hàm của hàm số lượng giác
Ví dụ 4. Tìm:
Hướng dẫn giải
4. Nguyên hàm của hàm số mũ
Với a > 0, a ≠ 1, ta có: .
Nhận xét: Áp dụng công thức trên, ta có: .
Ví dụ 5. Tìm:
Hướng dẫn giải
B. Bài tập Nguyên hàm của một số hàm số sơ cấp
Bài 1. bằng:
A. e4x + 1 + C.
B. e4x + C.
C. .
D. .
Hướng dẫn giải
Đáp án đúng là: D
Ta có: .
Bài 2. Tìm:
Hướng dẫn giải
Bài 3. Tìm:
Hướng dẫn giải
Bài 4. Một xe ô tô đang chạy với tốc độ 54 km/h thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó 50 m. Người la xe phản ứng một giây sau đó bằng cách đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ v(t) = – 10t + 20 (m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi s(t) là quãng đường xe ô tô đi được trong t (giây) kể từ lúc đạp phanh.
a) Lập công thức biểu diễn hàm số s(t).
b) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là bao nhiêu giây?
c) Quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là bao nhiêu mét? Xe ô tô liệu có gặp tai nạn do va chạm với chướng ngại vật trên đường hay không?
Hướng dẫn giải
a) Công thức tính quãng đường s(t) xe ô tô đi được trong t (giây) là một nguyên hàm của hàm v(t). Do nên ta có s(t) = – 5t2 + 20t + C với C là hằng số nào đó. Do s(0) = 0 nên C = 0. Suy ra s(t) = – 5t2 + 20t.
b) Xe ô tô dừng hẳn khi v(t) = 0, tức là – 10t + 20 = 0 hay t = 2.
Vậy thời gian kể từ lúc đạp phanh cho đến khi xe ô tô dừng hẳn là 2 giây.
c) Ta có: tốc độ 54 km/h cũng là tốc độ 15 m/s.
Do đó, quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là: s(2) = – 5 ∙ 22 + 20 ∙ 2 = 20 (m).
Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là: 15 + 20 = 35 (m).
Do 35 < 50 nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường. Vì thế, tai nạn đã không xảy ra đối với xe ô tô đó.
Bài 5. bằng:
A. sin x + C.
B. – sin x + C.
C. cos x + C.
D. – cos x + C.
Hướng dẫn giải
Đáp án đúng là: B
Ta có .
Xem thêm các chương trình khác:
- Soạn văn 12 Cánh diều (hay nhất)
- Văn mẫu 12 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 12 – Cánh diều
- Tác giả tác phẩm Ngữ văn 12 - Cánh diều
- Bố cục tác phẩm Ngữ văn 12 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn 12 – Cánh diều
- Giải sgk Tiếng Anh 12 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh lớp 12 ilearn Smart World đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh lớp 12 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 12 – iLearn Smart World
- Giải sgk Vật lí 12 – Cánh diều
- Giải Chuyên đề học tập Vật lí 12 – Cánh diều
- Lý thuyết Vật lí 12 – Cánh diều
- Giải sbt Vật lí 12 – Cánh diều
- Giải sgk Hóa học 12 – Cánh diều
- Giải Chuyên đề học tập Hóa 12 – Cánh diều
- Lý thuyết Hóa 12 – Cánh diều
- Giải sbt Hóa 12 – Cánh diều
- Giải sgk Sinh học 12 – Cánh diều
- Giải Chuyên đề học tập Sinh học 12 – Cánh diều
- Lý thuyết Sinh học 12 – Cánh diều
- Giải sbt Sinh học 12 – Cánh diều
- Giải sgk Lịch sử 12 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 12 – Cánh diều
- Giải sbt Lịch sử 12 – Cánh diều
- Giải sgk Địa lí 12 – Cánh diều
- Giải Chuyên đề học tập Địa lí 12 – Cánh diều
- Giải sbt Địa lí 12 – Cánh diều
- Giải sgk Tin học 12 – Cánh diều
- Giải Chuyên đề học tập Tin học 12 – Cánh diều
- Giải sbt Tin học 12 – Cánh diều
- Lý thuyết Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 – Cánh diều
- Giải sgk Kinh tế pháp luật 12 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 12 – Cánh diều
- Giải sbt Kinh tế pháp luật 12 – Cánh diều
- Giải sgk Giáo dục quốc phòng 12 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 – Cánh diều