Lý thuyết Ứng dụng hình học của Ứng dụng hình học của tích phân– Toán lớp 12 Cánh diều

Lý thuyết Toán 12 Bài 4: Ứng dụng hình học của tích phân- Cánh diều

A. Lý thuyết Ứng dụng hình học của tích phân

1. Tính diện tích hình phẳng

1.1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b

Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Khi đó, diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là:

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$.

Ví dụ 1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x² – 3x, trục hoành và hai đường thẳng x = 0, x = 3.

Hướng dẫn giải

Với mọi x ∈ [0; 3], ta có x² – 3x ≤ 0, do đó |x² – 3x| = – (x² – 3x) = 3x – x².

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x² – 3x, trục hoành và hai đường thẳng x = 0, x = 3 là:

$S=\underset{0}{\overset{3}{\int }}\left|x^2-3x\right|dx=\underset{0}{\overset{3}{\int }}\left(3x-x^2\right)dx={\left.\left(\frac{3}{2}{x}^2-\frac{x^3}{3}\right)\right|}_0^3=\frac{9}{2}$.

1.2. Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b

Cho các hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b]. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là:

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$.

Ví dụ 2. Tính diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y = x³ + 2x + 2, y = x³ + x + 3 và hai đường thẳng x = 0, x = 2.

Hướng dẫn giải

Diện tích hình phẳng đã cho là:

$S=\underset{0}{\overset{2}{\int }}\left|\left(x^3+2x+2\right)-\left(x^3+x+3\right)\right|dx$

$=\underset{0}{\overset{2}{\int }}\left|x-1\right|dx=\underset{0}{\overset{1}{\int }}\left|x-1\right|dx+\underset{1}{\overset{2}{\int }}\left|x-1\right|dx$

$=\underset{0}{\overset{1}{\int }}\left(1-x\right)dx+\underset{1}{\overset{2}{\int }}\left(x-1\right)dx$

$={\left.\left(x-\frac{x^2}{2}\right)\right|}_0^1+{\left.\left(\frac{x^2}{2}-x\right)\right|}_1^2$= 1.

2. Tính thể tích của hình khối

2.1. Thể tích của vật thể

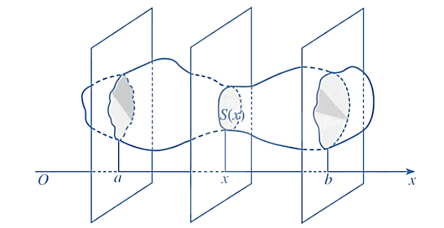
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x = a và x = b (a < b).

Một mặt phẳng tùy ý vuông góc với Ox tại x (a ≤ x ≤ b) cắt vật thể đó theo hình phẳng có diện tích là S(x). Giả sử hàm số S(x) liên tục trên [a; b]. Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng trên được tính bởi công thức

$V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$.

Chú ý: Nếu S(x) = S không đổi với mỗi x ∈ [a; b] thì V = (b – a)S.

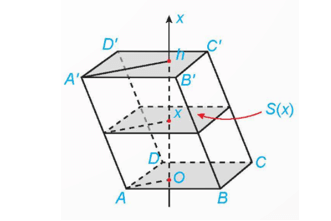
Ví dụ 3. Tính thể tích của khối lăng trụ có diện tích đáy bằng S và chiều cao bằng h.

Hướng dẫn giải

Chọn trục Ox song song với đường cao của khối lăng trục và hai đáy nằm trên hai mặt phẳng vuông góc với Ox tại x = 0 và x = h.

Mỗi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x (0 ≤ x ≤ h) cắt khối lăng trụ theo mặt cắt có diện tích không đổi là S(x) = S.

Do đó, thể tích của khối lăng trụ là V = (h – 0)S = Sh.

2.2. Thể tích của khối tròn xoay

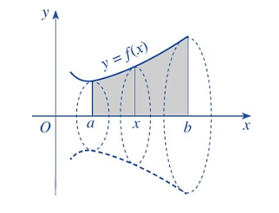
Cho hàm số y = f(x) liên tục, không âm trên đoạn [a; b]. Hình phẳng (H) giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng

$V=\pi \underset{a}{\overset{b}{\int }}{\left[f\left(x\right)\right]}^{2}dx$.

Ví dụ 4. Cho hình phẳng giới hạn bởi đồ thị hàm số y = x², trục hoành và hai đường thẳng x = 1, x = 3. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.

Hướng dẫn giải

Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số y = x², trục hoành và hai đường thẳng x = 1, x = 3, quay quanh trục Ox là:

$V=\pi \underset{1}{\overset{3}{\int }}{\left(x^2\right)}^{2}dx$$=\pi \underset{1}{\overset{3}{\int }}{x}^{4}dx={\left.\pi \frac{x^5}{5}\right|}_1^3=\pi \left(\frac{243}{5}-\frac{1}{5}\right)=\frac{242\pi }{5}$

B. Bài tập Ứng dụng hình học của tích phân

Bài 1. Cho hình phẳng giới hạn bởi đồ thị hàm số y = x + 1, trục hoành và hai đường thẳng x = 1, x = 3 quay quanh trục Ox được khối tròn xoay có thể tích tính theo công thức là:

A. $\underset{1}{\overset{3}{\int }}{\left(x+1\right)}^{2}dx$ .

B. $\pi \underset{1}{\overset{3}{\int }}{\left(x+1\right)}^{2}dx$ .

C. $\pi \underset{1}{\overset{3}{\int }}\left(x+1\right)dx$ .

D. $\underset{1}{\overset{3}{\int }}\left(x+1\right)dx$ .

Hướng dẫn giải

Đáp án đúng là: B

Thể tích khối tròn xoay được cho là:

$V=\pi \underset{1}{\overset{3}{\int }}{\left(x+1\right)}^{2}dx$.

Bài 2. Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = 3^x, trục hoành và hai đường thẳng x = 1, x = 3.

a) Tính diện tích S của hình phẳng H.

b) Tính thể tích V của khối tròn xoay tạo thành khi cho hình phẳng H quay quanh trục Ox.

Hướng dẫn giải

a) Diện tích của hình phẳng H là:

$S=\underset{1}{\overset{3}{\int }}\left|3^x\right|dx=\underset{1}{\overset{3}{\int }}{3}^{x}dx={\left.\frac{3^x}{\ln 3}\right|}_1^3=\frac{24}{\ln 3}$.

b) Thể tích khối tròn xoay tạo thành khi cho hình phẳng H quay quanh trục Ox là:

$V=\pi \underset{1}{\overset{3}{\int }}{\left(3^x\right)}^{2}dx$$=\pi \underset{1}{\overset{3}{\int }}{9}^{x}dx={\left.\pi \frac{9^x}{\ln 9}\right|}_1^3=\frac{\pi }{2\ln 3}\left(9^3-9\right)=\frac{360}{\ln 3}$.

Bài 3. Cho hình phẳng giới hạn bởi đồ thị hàm số f(x) = $\cos \frac{x}{2}$ , trục hoành và hai đường thẳng x = 0, x = $\frac{\pi }{2}$ . Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.

Hướng dẫn giải

Thể tích tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số f(x) = $\cos \frac{x}{2}$ , trục hoành và hai đường thẳng x = 0, x = $\frac{\pi }{2}$ , quay quanh trục Ox là:

$V=\pi \underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^2\frac{x}{2}dx$$=\pi \underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1+\cos x}{2}dx$$=\frac{\pi }{2}\left(\underset{0}{\overset{\frac{\pi }{2}}{\int }}dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\cos xdx\right)$

$=\frac{\pi }{2}\left({\left.x\right|}_0^{\frac{\pi }{2}}+{\left.\sin x\right|}_0^{\frac{\pi }{2}}\right)$$=\frac{\pi }{2}\left(\frac{\pi }{2}+\sin \frac{\pi }{2}-\sin 0\right)=\frac{{\pi }^2}{4}+\frac{\pi }{2}$

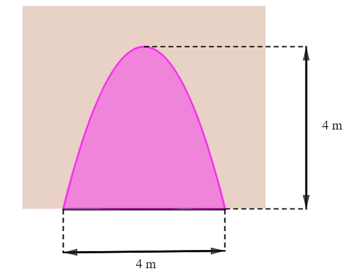
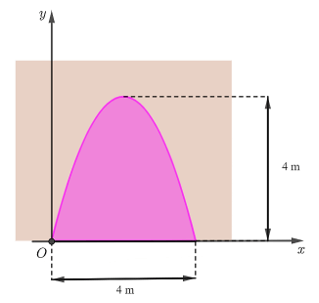
Bài 4. Mặt cắt của một cửa hầm có dạng là một hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình dưới đây.

Tính diện tích của cửa hầm.

Hướng dẫn giải

Chọn hệ trục tọa độ Oxy như hình vẽ trên. Khi đó, parabol đi qua các điểm có tọa độ (0; 0), (2; 4) và (4; 0).

Giả sử parabol có dạng y = ax² + bx + c (a ≠ 0).

Vì parabol đi qua các điểm có tọa độ (0; 0), (2; 4) và (4; 0) nên ta có:

$\left\{\begin{array}{l}c=0\\ 4a+2b+c=4\\ 16a+4b+c=0\end{array}\right.\iff \left\{\begin{array}{l}a=-1\\ b=4\\ c=0\end{array}\right.$.

Do đó, parabol có phương trình là y = – x² + 4x.

Diện tích của cửa hầm là diện tích hình phẳng giới hạn bởi parabol y = – x² + 4x, trục hoành và hai đường thẳng x = 0, x = 4.

Vậy diện tích của cửa hầm là:

$S=\underset{0}{\overset{4}{\int }}\left|-x^2+4x\right|dx$$=\underset{0}{\overset{4}{\int }}\left(-x^2+4x\right)dx$$={\left.\left(-\frac{x^3}{3}+2x^2\right)\right|}_0^4=\frac{32}{3}$.

Bài 5. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x, y = x³ và hai đường thẳng x = 1, x = 2 là:

A. $\underset{1}{\overset{2}{\int }}\left(x-x^3\right)dx$ .

B. $\underset{1}{\overset{2}{\int }}xdx-\underset{1}{\overset{2}{\int }}{x}^{3}dx$ .

C. $\underset{1}{\overset{2}{\int }}{x}^{3}dx-\underset{1}{\overset{2}{\int }}xdx$ .

D. $\underset{1}{\overset{2}{\int }}\left(x^3+x\right)dx$ .

Hướng dẫn giải

Đáp án đúng là: C

Với x ∈ [1; 2], x – x³ ≤ 0, do đó |x – x³| = x³ – x.

Khi đó, diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x, y = x³ và hai đường thẳng x = 1, x = 2 là:

$S=\underset{1}{\overset{2}{\int }}\left|x-x^3\right|dx=\underset{1}{\overset{2}{\int }}\left(x^3-x\right)dx=\underset{1}{\overset{2}{\int }}{x}^{3}dx-\underset{1}{\overset{2}{\int }}xdx$.