Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Toán lớp 12 Cánh diều

Lý thuyết Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Cánh diều

A. Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

1. Định nghĩa giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Cho hàm số y = f(x) xác định trên tập D.

- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D, kí hiệu $M=\underset{D}{\max }f\left(x\right)$, nếu f(x) ≤ M với mọi x ∈ D và tồn tại x₀ ∈ D sao cho f(x₀) = M.

- Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D, kí hiệu $m=\underset{D}{\min }f\left(x\right)$, nếu f(x) ≥ m với mọi x ∈ D và tồn tại x₁ ∈ D sao cho f(x₁) = m.

Chú ý: Khi tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số mà không chỉ rõ tập D thì ta tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số đó trên cả tập xác định của nó.

Ví dụ 1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) = 2x² + 3 trên đoạn [1; 3].

Hướng dẫn giải

Do 1 ≤ x² ≤ 9 với mọi x ∈ [1; 3] nên 5 ≤ 2x² + 3 ≤ 21 với mọi x ∈ [1; 3],

tức là 5 ≤ f(x) ≤ 21 với mọi x ∈ [1; 3].

Ta có f(1) = 5 nên $\underset{\left(1;3\right)}{\min }f\left(x\right)=5;$ f(3) = 21 nên $\underset{\left(1;3\right)}{\max }f\left(x\right)=21.$

2. Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số bằng đạo hàm

* Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) trên một khoảng, đoạn hay nửa khoảng, ta có thể lập bảng biến thiên của hàm số trên tập hợp đó. Căn cứ vào bảng biến thiên, ta tìm được giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

Ví dụ 2. Tìm giá trị nhỏ nhất và giá trị lớn nhất (nếu có) của hàm số $y=x-5+\frac{1}{x}$ trên khoảng (0; + ∞).

Hướng dẫn giải

Xét hàm số $y=x-5+\frac{1}{x}$ với x ∈ (0; + ∞).

Ta có $y\text{'}=1-\frac{1}{x^2}.$ Khi đó, trên khoảng (0; + ∞), y' = 0 khi x = 1.

Ngoài ra, $\underset{x\to 0^{+}}{\lim }y=+\infty ;\underset{x\to +\infty }{\lim }y=+\infty$

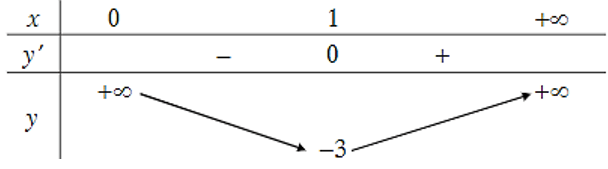
Bảng biến thiên của hàm số như sau:

Căn cứ vào bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }y=-3$ tại x = 1 và hàm số đã cho không có giá trị lớn nhất.

* Nhận xét: Người ta chứng minh được rằng: Mọi hàm số liên tục trên một đoạn đều có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn đó.

Giả sử hàm số f(x) liên tục trên đoạn [a; b] và có đạo hàm trên khoảng (a; b), có thể trừ một số hữu hạn điểm. Nếu f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc khoảng (a; b) thì ta có quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b] như sau:

Bước 1. Tìm các điểm x₁, x₂, …, x_n thuộc khoảng (a; b) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

Bước 2. Tính f(x₁), f(x₂), …, f(x_n), f(a) và f(b).

Bước 3. So sánh các giá trị tìm được ở Bước 2.

Số lớn nhất trong các giá trị đó là giá trị lớn nhất của hàm số f(x) trên đoạn [a; b], số nhỏ nhất trong các giá trị đó là giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b].

Ví dụ 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:

a) f(x) = – x⁴ + 12x² + 1 trên đoạn [– 1; 2];

b) f(x) = x² + $\frac{2}{x}$ trên đoạn [2; 3].

Hướng dẫn giải

a) Ta có f'(x) = – 4x³ + 24x.

Khi đó, trên khoảng (– 1; 2), f'(x) = 0 khi x = 0.

f(– 1) = 12; f(0) = 1; f(2) = 33.

Vậy $\underset{\left(-1;2\right)}{\max }f\left(x\right)=33$ tại x = 2; $\underset{\left(-1;2\right)}{\min }f\left(x\right)=1$ tại x = 0.

b) Ta có f'(x) = 2x – $\frac{2}{x^2}$

Khi đó, trên khoảng [2; 3], không có giá trị của x để f'(x) = 0.

f(2) = 5; f(3) = .

Vậy $\underset{\left(2;3\right)}{\max }f\left(x\right)=\frac{29}{3}$ tại x = 3; $\underset{\left(2;3\right)}{\min }f\left(x\right)=5$ tại x = 2.

B. Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 1. Giá trị lớn nhất của hàm số f(x) = (x – 3)² ∙ e^x trên đoạn [2; 4] là

A. 0.

B. e².

C. e³.

D. e⁴.

Hướng dẫn giải

Đáp án đúng là: D

Ta có f'(x) = 2(x – 3) ∙ e^x + (x – 3)² ∙ e^x = (x – 3) ∙ e^x ∙ (x – 1).

Khi đó, trên khoảng (2; 4), f'(x) = 0 khi x = 3.

f(2) = e²; f(3) = 0; f(4) = e⁴.

Vậy $\underset{\left(2;4\right)}{\max }f\left(x\right)=e^4$ tại x = 4.

Bài 2. Tìm giá trị nhỏ nhất của hàm số y = x – 2 + $\frac{1}{x}$ trên khoảng (0; + ∞).

Hướng dẫn giải

Xét hàm số $y=x-5+\frac{1}{x}$ với x ∈ (0; + ∞).

Ta có y' = 1 $-\frac{1}{x^2}$. Khi đó, trên khoảng (0; + ∞), y' = 0 khi x = 1.

Ngoài ra, $\underset{x\to 0^{+}}{\lim }y=+\infty ;\underset{x\to +\infty }{\lim }y=+\infty$

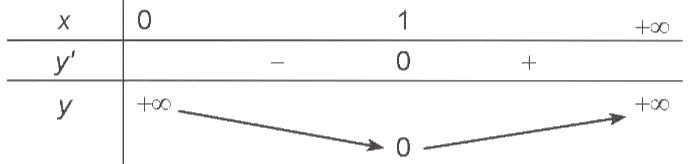
Bảng biến thiên của hàm số như sau:

Căn cứ vào bảng biến thiên, ta có tại x = 1.

Bài 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:

a) f(x) = x³ – 3x + 5 trên đoạn [0; 2];

b) f(x) = x – sin 2x trên đoạn [0; π].

Hướng dẫn giải

a) Ta có f'(x) = 3x² – 3. Khi đó trên khoảng (0; 2), f'(x) = 0 khi x = 1.

f(0) = 5; f(1) = 3; f(2) = 7.

Vậy $\underset{\left(0;2\right)}{\max }f\left(x\right)=7$ tại x = 2; $\underset{\left(0;2\right)}{\min }f\left(x\right)=3$ tại x = 1.

b) Ta có f'(x) = 1 – 2cos 2x.

Khi đó trên khoảng (0; π), f'(x) = 0 khi x = $\frac{\pi }{6}$ hoặc x = $\frac{5\pi }{6}$

f(0) = 0; $f\left(\frac{\pi }{6}\right)=\frac{\pi }{6}-\frac{\sqrt{3}}{2}$; $f\left(\frac{5\pi }{6}\right)=\frac{5\pi }{6}+\frac{\sqrt{3}}{2}$; f(π) = π.

Vậy $\underset{\left(0;\pi \right)}{\max }f\left(x\right)=\frac{5\pi }{6}+\frac{\sqrt{3}}{2}$ tại $x=\frac{5\pi }{6}$; $\underset{\left(0;\pi \right)}{\min }f\left(x\right)=\frac{\pi }{6}-\frac{\sqrt{3}}{2}$ tại $x=\frac{\pi }{6}$

Bài 4. Khi xây nhà, chủ nhà cần làm một bồn nước bằng gạch và xi măng có dạng hình hộp đứng đáy là hình chữ nhật có chiều rộng là x (m), chiều dài gấp 2 lần chiều rộng và không nắp, có chiều cao là h (m), có thể tích là $\frac{4}{3}$m³. Tìm chiều rộng của đáy hình chữ nhật để chi phí xây dựng là thấp nhất.

Hướng dẫn giải

Chiều dài hình chữ nhật là 2x (m).

Ta có $V=\frac{4}{3}\iff x\cdot 2x\cdot h=\frac{4}{3}\iff h=\frac{2}{3x^2}$

Diện tích xung quanh của bồn nước (không nắp) là

S = 2(xh + 2xh) + 2x² = 6xh + 2x² = $\frac{4}{x}$ + 2x² (m²) với x > 0.

Xét hàm số S(x) = $\frac{4}{x}$ + 2x² với x ∈ (0; + ∞).

Ta có $S\text{'}\left(x\right)=-\frac{4}{x^2}+4x$ ; S'(x) = 0 ⇔ x = 1 ∈ (0; + ∞).

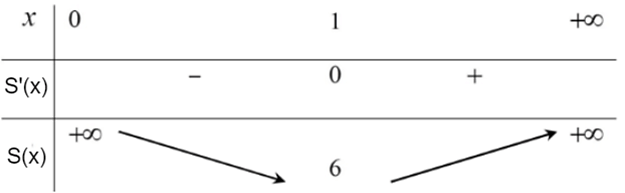
Bảng biến thiên của hàm số như sau:

Căn cứ vào bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }S\left(x\right)=6$ tại x = 1.

Để chi phí xây dựng là thấp nhất thì diện tích xung quanh của bồn nước phải nhỏ nhất.

Vậy chiều rộng của đáy hình chữ nhật bằng 1 m thì chi phí xây dựng là thấp nhất.

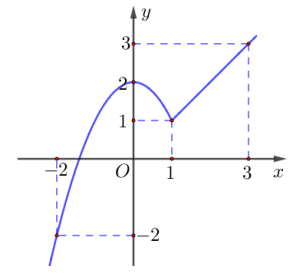
Bài 5. Cho hàm số y = f(x), x ∈ [– 2; 3] có đồ thị như hình vẽ dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [– 2; 3].

Giá trị S = M + m là

A. 3.

B. 1.

C. 6.

D. 5.

Hướng dẫn giải

Đáp án đúng là: B

Từ đồ thị, ta có M = 3 và m = – 2. Suy ra, S = M + m = 3 + (– 2) = 1.