Trắc nghiệm Toán 10 Bài tập cuối chương 5 có đáp án
Trắc nghiệm Toán 10 Bài tập cuối chương 5 có đáp án
-
441 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có .
.
Vậy ta chọn đáp án B.
Câu 2:
21/07/2024Cho M, N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ bằng vectơ nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
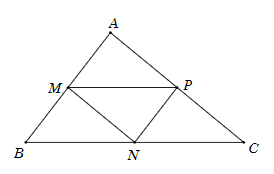
Tam giác ABC có N, P lần lượt là trung điểm BC và AC.
Do đó NP là đường trung bình của tam giác ABC.
Suy ra NP = BM (M là trung điểm AB).
Mà cùng hướng.
Do đó .
Ta có .
Vậy ta chọn đáp án B.
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Đáp án A đúng theo tính chất phân phối của tích vô hướng.
Đáp án B sai. Sửa lại: .
Đáp án C đúng theo tính chất giao hoán của tích vô hướng.
Đáp án D đúng theo bình phương vô hướng và hằng đẳng thức.
Câu 4:
19/07/2024Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm BC. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì M là trung điểm BC nên ta có .
Khi đó
.
Vậy ta chọn đáp án A.
Câu 5:
23/07/2024Nếu thì
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
A, B, C là ba điểm thẳng hàng và B, C nằm cùng phía so với A.
Mà AB = AC nên B ≡ C.
Câu 6:
18/07/2024Cho hình vuông ABCD tâm O. Tính tổng .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
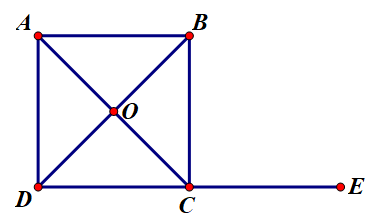
Ta có cùng hướng nên .
Ta có ngược hướng nên .
Vẽ . Khi đó ta có .
Vì ABCD là hình vuông có OC là đường chéo nên .
Ta có BC ⊥ CD (ABCD là hình vuông)
Suy ra BC ⊥ CE, do đó .
Ta có .
Vậy .
Vậy ta chọn đáp án C.
Câu 7:
23/07/2024Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
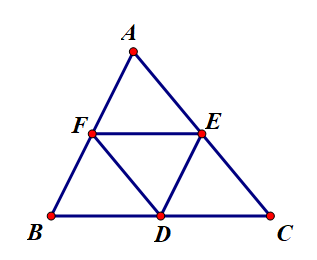
Ta có
Vậy ta chọn đáp án C.
Câu 8:
22/07/2024Cho hai vectơ không cùng phương và . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vì cùng phương với mọi vectơ nên có một vectơ cùng phương với cả hai vectơ và , đó là .
Câu 9:
18/07/2024Cho tam giác ABC và một điểm M tùy ý. Cho . Hãy xác định vị trí của điểm D sao cho .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có (với I là trung điểm AB).
Do đó không phụ thuộc vào vị trí của điểm M.
Khi đó .
Suy ra I là trung điểm CD.
Vậy D là điểm thứ tư của hình bình hành ACBD.
Vậy ta chọn đáp án B.
Câu 10:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta xét từng đáp án:
Đáp án A: ⇒ loại A.
Đáp án B: (với D là điểm thỏa mãn tứ giác ABDC là hình bình hành).
Mà AD và BC là 2 đường chéo của hình bình hành ABDC.
Do đó ⇒ loại B.
Đáp án C: (đúng) ⇒ chọn C.
Đáp án D: (khi cộng hai vectơ theo quy tắc 3 điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai) ⇒ loại D.
Vậy ta chọn đáp án C.
Câu 11:
21/07/2024Cho tam giác ABC. Tập hợp các điểm M thỏa mãn là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có .
Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.
Vậy ta chọn đáp án B.
Câu 12:
29/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
Vì tam giác ABC đều cạnh 2a nên .
*Phương pháp giải
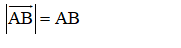
*Lý thuyết
- Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vectơ chính bằng độ dài đoạn thẳng AB. Kí hiệu:
- Độ dài của vectơ được tính theo công thức: .
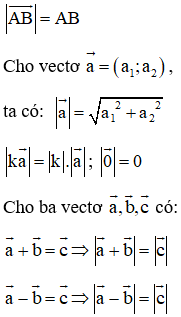
Xem thêm
Câu 13:
07/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
*Phương pháp giải:
- Áp dụng quy tắc hình bình hành để xác định được tổng của hai vecto.
- Dựa vào các tính chất của hình thoi và dữ kiện đề bài đã cho để xác định số đo của các cạnh.
- Sử dụng định lí Pytago để tìm ra độ dài đoạn cần tính.
*Lời giải:
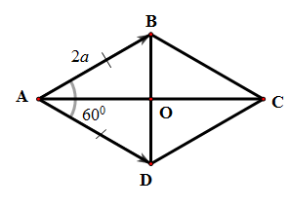
Tứ giác ABCD là hình thoi ⇒ AB = AD.
Do đó tam giác ABD cân tại A.
Mà .
Suy ra tam giác ABD là tam giác đều.
⇒ BD = AB = AD = 2a.
Theo quy tắc hình bình hành, ta có .
Suy ra .
Vì O là tâm hình thoi ABCD nên O là trung điểm AC và BD.
Do đó AC = 2AO và BO = = a.
Tam giác ABO vuông tại O: (Định lý Pytago)
.
.
Do đó .
Xem thêm các bài viết liên quan hay, chi tiết:
Giải SGK Toán 10 Bài 8: Tổng và hiệu của hai vectơ
Công thức về tổng và hiệu hai vectơ chi tiết nhất - Toán lớp 10
Câu 14:
23/07/2024Cho hai vectơ và khác . Xác định góc α giữa hai vectơ và khi .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có .
Mà theo giả thiết, ta có
Suy ra .
Do đó .
Vậy ta chọn đáp án A.
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
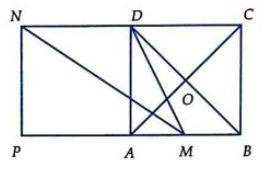
Vì M là trung điểm AB nên ta có AM = .
Tam giác MAD vuông tại A: (Định lý Pytago)
.
Qua N kẻ đường thẳng song song với AD cắt AB tại P.
Ta có NP // AD, mà AD ⊥ CN (vì ABCD là hình vuông)
Do đó NP ⊥ CN hay NP ⊥ ND.
Suy ra (1).
Vì AD ⊥ ND nên (2).
Tương tự, AD ⊥ AP nên (3).
Từ (1) (2) (3), ta suy ra tứ giác ADNP là hình chữ nhật (4).
Vì N là điểm đối xứng của C qua D nên ND = CD = a.
Mà AD = a (do ABCD là hình vuông cạnh a).
Nên ND = AD = a (5).
Từ (4) (5), ta suy ra ADNP là hình vuông.
Do đó AP = AD = a.
Ta có PM = PA + AM = a + .
Tam giác NPM vuông tại P: : (Định lý Pytago)
.
Suy ra .
Vậy ta chọn đáp án C.
Câu 16:
27/11/2024Cho ba điểm phân biệt A, B, C. Nếu thì đẳng thức nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Lời giải

Từ đẳng thức , ta suy ra ba điểm A, B, C thẳng hàng.
Vì k = – 3 < 0 nên và ngược hướng. Do đó điểm A nằm giữa hai điểm B và C.
Ta có , suy ra , do đó AB = 3AC.
Suy ra BC = AB + AC = 3AC + AC = 4AC.
Mà cùng hướng.
Do đó ta suy ra .
*Phương pháp giải
Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Hai vectơ và được gọi là bằng nhau, kí hiệu là = , nếu chúng có cùng độ dài và cùng hướng.
*Lý thuyết
Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
+ Hai vectơ và được gọi là bằng nhau, kí hiệu là = , nếu chúng có cùng độ dài và cùng hướng.
Ví dụ:

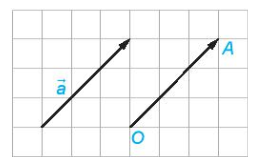
Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ , nên đường thẳng m gọi là giá của vectơ .
Tương tự, đường thẳng n là giá của hai vectơ và .
Đường thẳng m và n song song với nhau nên ba vectơ và và là các vectơ cùng phương.
và cùng phương nhưng ngược hướng; và cùng phương và cùng hướng.
Hai vectơ và cùng hướng, ngoài ra chúng có độ dài bằng nhau nên = .
Chú ý:
+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn , ), gọi là các vectơ–không.
+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là .
+ Với mỗi điểm O và vectơ cho trước, có duy nhất điểm A sao cho .
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi và cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
Xem thêm các bài toán hay, chi tiết khác
Lý thuyết Toán 10 Bài 7: Các khái niệm mở đầu - Kết nối tri thức
Câu 17:
10/10/2024Cho hình thoi ABCD có AC = 8 và BD = 6. Tính .
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
*Phương pháp giải:
- Vì giả thiết không cho góc nên ta sẽ phân tích các vectơ theo các vectơ vuông góc với nhau.
- Trong hình thoi 2 đường chéo sẽ vuông góc, mà tích 2 vecto vuông góc = 0.Sau đó tách thành các vecto dựa vào quy tắc 3 điểm để sử dụng được dữ kiện bài toán cho
*Lời giải:
Gọi O là giao điểm của AC và BD.
Khi đó O là trung điểm của AC và BD.
Vì ABCD là hình thoi nên AC ⊥ BD hay AC ⊥ OB.
Suy ra .
Do đó .
Ta có
.
*Công thức cần nắm thêm:
- Quy tắc trung điểm: I là trung điểm của AB
−−→MA+−−→MB=2−−→MI ( M tùy ý )
- Quy tắc trọng tâm: G là trọng tâm tam giác ABC
−−→MA+−−→MB+−−→MC=3−−→MG ( M tùy ý )
- Quy tắc ba điểm: −−→AB+−−→BC=−−→AC.
- Phân tích một vectơ theo hai vectơ →a và →b không cùng phương: →x=h→a+k→b (h, k là duy nhất)
- Độ dài vectơ tích của vectơ với một số: ∣∣k→a∣∣=|k|.∣∣→a∣∣
- Điều kiện 2 vectơ →a và →b(→b≠0) cùng phương: →a=k→b ( k≠0)
- Điều kiện 3 điểm thẳng hàng: −−→AB=k−−→AC
- Tính chất của tích vectơ với một số:
k(→a+→b)=k→a+k→b(h+k)→a=h→a+k→ah(k→a)=(hk)→a1.→a=→a;(−1)→a=−→a0.→a=→0; k.→0=→0
Xem thêm các bài viết liên quan hay, chi tiết
Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Tổng hợp)
Câu 18:
19/07/2024Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Đáp án A, B, C đúng.
Đáp án D chỉ đúng khi B nằm giữa hai điểm A và C.
Vậy ta chọn đáp án D.
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta xét từng đáp án:
Đáp án A: Tứ giác ABCO là hình bình hành nên theo quy tắc hình bình hành, ta có .
Vì O là trung điểm BE nên .
Do đó ta có .
Vậy A đúng.
Đáp án B: Ta có và .
Do đó .
Vậy B đúng.
Đáp án C: Ta có (2 vectơ này cùng hướng và có độ dài bằng nhau).
Ta có
Vậy C đúng.
Đáp án D: Vì tứ giác ABOF là hình bình hành nên .
Vì tứ giác CDEO là hình bình hành nên .
Do đó ta có
Vậy D sai.
Vậy ta chọn đáp án D.
Câu 20:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
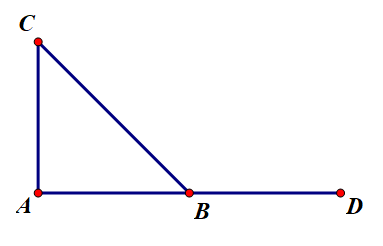
Vẽ .
Ta có .
Tam giác ABC vuông cân tại A. Ta suy ra .
Ta có (hai góc kề bù)
Khi đó ta được .
Tam giác ABC vuông cân tại A: BC2 = AB2 + AC2 (Định lý Pytago)
⇔ BC2 = 2a2
.
Do đó
Vậy ta chọn đáp án A.
Câu 21:
23/07/2024Cho và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn và . Tìm ![]() .
.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có .
Câu 22:
17/07/2024Cho thì số vectơ cùng phương với vectơ đã cho là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Giá của vectơ là đường thẳng MN, mà có vô số đường thẳng song song và trùng với đường thẳng MN.
Do đó có vô số vectơ cùng phương với .
Câu 23:
21/07/2024Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
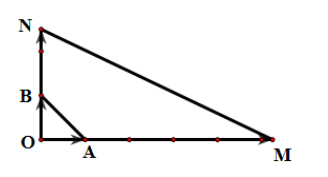
Dựng điểm M, N sao cho và . Khi đó ta có:
.
Từ dữ kiện .
Ta suy ra cùng phương với .
Vì có cùng điểm đầu là O.
Nên giá của trùng nhau.
Do đó ta có OM ≡ OA.
Tương tự ta có ON ≡ OB.
Mà OA ⊥ OB (tam giác OAB vuông cân tại O).
Do đó OM ⊥ ON.
Ta có .
Tương tự, ta có .
Tam giác OMN vuông tại O: (Định lý Pytago)
.
Vậy ta chọn đáp án D.
Câu 24:
22/07/2024Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Hỏi bằng vectơ nào trong các vectơ sau đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
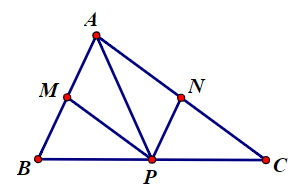
Tam giác ABC có M, P lần lượt là trung điểm của các cạnh AB, BC.
Do đó MP là đường trung bình của tam giác ABC.
Suy ra MP //AC và MP = = AN (N là trung điểm AC).
Do đó .
Ta có .
Vậy ta chọn đáp án C.
Câu 25:
18/07/2024Cho đường tròn (O). Từ điểm A nằm ngoài (O), kẻ hai tiếp tuyến AB, AC tới (O). Xét các mệnh đề sau:
(I) (II) (III)
Mệnh đề đúng là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
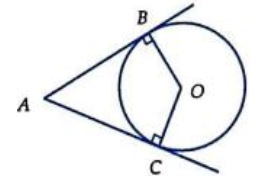
Mệnh đề (I) sai vì không cùng phương.
Mệnh đề (II) sai vì không cùng phương.
Mệnh đề (III) đúng vì:
Ta có OB, OC là bán kính đường tròn (O) nên OB = OC = R.
Mà và nên ta có .
Vậy ta chọn đáp án D.
Câu 26:
23/07/2024Tập hợp các điểm M thỏa mãn với A, B, C là ba đỉnh của tam giác là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi G là trọng tâm tam giác ABC. Ta suy ra .
Ta có (*)
Biểu thức (*) chứng tỏ MB ⊥ MG hay M nhìn đoạn BG dưới một góc vuông.
Do đó tập hợp các điểm M là một đường tròn đường kính BG.
Vậy ta chọn đáp án D
Câu 27:
23/07/2024Cho hình chữ nhật ABCD, biết AB = 4a, AD = 3a. Tính độ dài .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
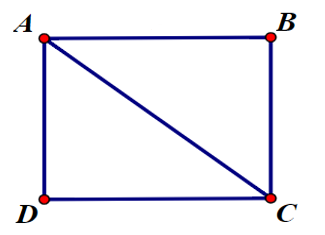
Vì ABCD là hình vuông nên BC = AD = 3a.
Theo quy tắc hình bình hành, ta có: .
Tam giác ABC vuông tại B: (Định lý Pytago)
⇒ AC = 5a.
Do đó .
Vậy ta chọn đáp án D.
Câu 28:
09/12/2024Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh của tứ giác?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Lời giải
Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.
Vectơ khác vectơ-không là vectơ có điểm đầu khác điểm cuối.
Các vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C, D là: .
Do đó có 12 vectơ thỏa mãn yêu cầu bài toán.
*Phương pháp giải:
Chọn điểm đầu là một trong điểm, đếm số véc tơ có điểm đầu là điểm vừa chọn và điểm cuối là các điểm còn lại.
Từ đó suy ra số véc tơ thỏa mãn bài toán.
*Lý thuyết:
1. Khái niệm vectơ
Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.
Định nghĩa: Vectơ là một đoạn thẳng có hướng.
Vectơ có điểm đầu A, điểm cuối B được kí hiệu là và đọc là “vectơ AB”. Để vẽ được vectơ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.
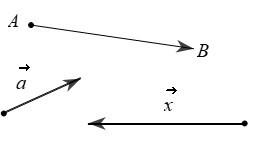
Đối với vectơ , ta gọi:
– Đường thẳng d đi qua hai điểm A và B là giá của vectơ .
– Độ dài đoạn thẳng AB là độ dài của vectơ , kí hiệu là .
Vectơ còn được kí hiệu là , , , khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ được kí hiệu là
Ví dụ: Vectơ có độ dài là 5, ta có thể viết như sau: = 5.
Xem thêm
Câu 29:
19/07/2024Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
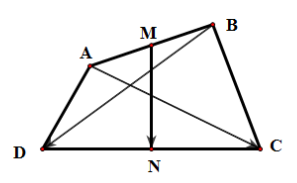
Vì M là trung điểm AB nên .
Vì N là trung điểm CD nên .
Theo quy tắc ba điểm, ta có
Suy ra
Vậy ta chọn đáp án B.
Câu 30:
20/07/2024Cho hai lực và cùng tác động vào một vật đứng tại điểm O, biết hai lực và đều có cường độ là 50 (N) và chúng hợp với nhau một góc 60°. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
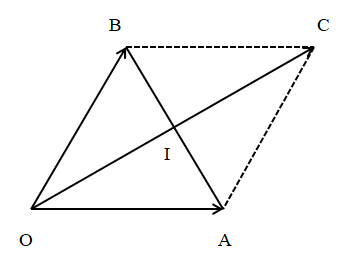
Đặt và . Khi đó ta có = 50 (N) và .
Dựng điểm C sao cho tứ giác OACB là hình bình hành.
Theo quy tắc hình bình hành, ta có: hay .
Suy ra lực tổng hợp của hai lực và là .
Do đó cường độ tổng hợp lực của hai lực và là .
Vì OA = OB nên tam giác OAB cân tại O.
Mà nên tam giác OAB đều.
Gọi I là giao điểm của OC và AB
⇒ I là trung điểm OC và AB ⇒ BI = = 25 (N).
Tam giác OAB đều có OI là đường trung tuyến.
Suy ra OI cũng là đường cao của tam giác OAB.
Tam giác OBI vuông tại I: (Định lý Pytago)
⇒ OI = (N).
Do đó OC = 2OI = (N).
Vậy ta chọn đáp án B.
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài tập cuối chương 5 có đáp án (440 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài tập cuối chương 5 có đáp án (Phần 2) (417 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 CTST Bài 1. Khái niệm vectơ có đáp án (Phần 2) (527 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2. Tổng và hiệu của hai vectơ có đáp án (Phần 2) (487 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án (Phần 2) (416 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Khái niệm vectơ có đáp án (364 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Tích vô hướng của hai vectơ có đáp án (361 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Tích của một số với một vectơ có đáp án (356 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án (Phần 2) (292 lượt thi)
- Trắc nghiệm Toán 10 Bài 2. Tổng và hiệu của hai vectơ có đáp án (260 lượt thi)
