15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 3. Tích của một số với một vectơ có đáp án

Câu 1:

23/07/2024

Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài $\vec{C B} + \vec{A B}$ .

A. $\sqrt{13}$

B. $2 \sqrt{13}$

C. $2 \sqrt{3}$

D. $\sqrt{3}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

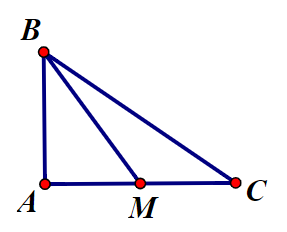
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài vecto CB+AB (ảnh 1)

Gọi M là trung điểm AC, ta suy ra $\vec{M A} + \vec{M C} = \vec{0}$ .

\Leftrightarrow - \vec{A M} - \vec{C M} = \vec{0}

\Leftrightarrow - (\vec{A M} + \vec{C M}) = \vec{0}

\Leftrightarrow \vec{A M} + \vec{C M} = \vec{0}

Ta có $\vec{C B} + \vec{A B} = \vec{C M} + \vec{M B} + \vec{A M} + \vec{M B} = (\vec{A M} + \vec{C M}) + 2 \vec{M B} = \vec{0} + 2 \vec{M B} = 2 \vec{M B}$ .

Vì M là trung điểm AC nên AM = $\frac{A C}{2}$ = 2.

Tam giác ABM vuông tại A: $B M^{2} = A B^{2} + A M^{2}$ (Định lý Pytago)

\Leftrightarrow B M^{2} = 3^{2} + 2^{2} = 13

\Rightarrow B M = \sqrt{13}

Ta suy ra $|\vec{C B} + \vec{A B}| = |2 \vec{M B}| = 2. M B = 2 \sqrt{13}$ .

Vậy ta chọn đáp án B.

Câu 2:

23/07/2024

Cho $\vec{a} \neq \vec{0}$ và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn $\vec{O M} = 3 \vec{a}$ và $\vec{O N} = - 4 \vec{a}$ . Tìm $\vec{M N}$ .

A. $\vec{M N} = 7 \vec{a}$

B. $\vec{M N} = 5 \vec{a}$

C. $\vec{M N} = - 7 \vec{a}$

D. $\vec{M N} = - 5 \vec{a}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\vec{M N} = \vec{O N} - \vec{O M} = - 4 \vec{a} - 3 \vec{a} = - 7 \vec{a}$ .

Câu 3:

22/07/2024

Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?

A. $\vec{A G} = \frac{1}{2} \vec{A E} + \frac{1}{2} \vec{AF}$

B. $\vec{A G} = \frac{1}{3} \vec{A E} + \frac{1}{3} \vec{AF}$

C. $\vec{A G} = \frac{3}{2} \vec{A E} + \frac{3}{2} \vec{AF}$

D. $\vec{A G} = \frac{2}{3} \vec{A E} + \frac{2}{3} \vec{AF}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

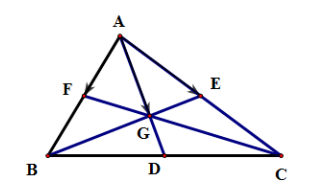
Vì G là trọng tâm của tam giác ABC nên ta có $\vec{A G} = \frac{2}{3} \vec{A D}$ .

Tam giác ABC có D là trung điểm cạnh BC, suy ra $2 \vec{A D} = \vec{A B} + \vec{A C}$ .

Ta có E, F lần lượt là trung điểm AC, AB.

Suy ra $\vec{A C} = 2 \vec{A E}$ và $\vec{A B} = 2 \vec{A F}$ .

Khi đó ta có $\vec{A G} = \frac{2}{3} \vec{A D} = \frac{1}{3} (\vec{A B} + \vec{A C}) = \frac{1}{3} (2 \vec{A F} + 2 \vec{A E}) = \frac{2}{3} \vec{A E} + \frac{2}{3} \vec{A F}$ .

Vậy ta chọn đáp án D.

Câu 4:

21/07/2024

Cho ba điểm phân biệt A, B, C. Nếu $\vec{A B} = - 3 \vec{A C}$ thì đẳng thức nào dưới đây đúng?

A. $\vec{B C} = - 4 \vec{A C}$

B. $\vec{B C} = - 2 \vec{A C}$

C. $\vec{B C} = 2 \vec{A C}$

D. $\vec{B C} = 4 \vec{A C}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Từ đẳng thức $\vec{A B} = - 3 \vec{A C}$ , ta suy ra ba điểm A, B, C thẳng hàng.

Vì k = – 3 < 0 nên $\vec{A B}$ và $\vec{A C}$ ngược hướng. Do đó điểm A nằm giữa hai điểm B và C.

Ta có $\vec{A B} = - 3 \vec{A C}$ , suy ra $|\vec{A B}| = |- 3 \vec{A C}|$ , do đó AB = 3AC.

Suy ra BC = AB + AC = 3AC + AC = 4AC.

Mà $\vec{B C}, \vec{A C}$ cùng hướng.

Do đó ta suy ra $\vec{B C} = 4 \vec{A C}$ .

Vậy ta chọn đáp án D.

Câu 5:

21/07/2024

Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?

A. $\vec{A B} + \vec{A D} = \vec{A C}$

B. $\vec{O A} = \frac{1}{2} (\vec{B A} + \vec{C B})$

C. $\vec{O A} + \vec{O B} = \vec{O C} + \vec{O D}$

D. $\vec{O A} + \vec{O B} = \vec{D A}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

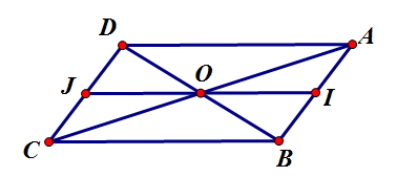
Ta xét từng đáp án:

Đáp án A: Theo quy tắc hình bình hành, ta có $\vec{A B} + \vec{A D} = \vec{A C}$ ⇒ A đúng.

Đáp án B: Vì O là tâm của hình bình hành ABCD nên O là trung điểm AC.

Ta suy ra $O A = \frac{1}{2} C A$ .

Mà $\vec{O A}, \vec{C A}$ cùng hướng.

Do đó $\vec{O A} = \frac{1}{2} \vec{C A} = \frac{1}{2} (\vec{C B} + \vec{B A})$ ⇒ B đúng.

Đáp án C: Gọi I, J lần lượt là trung điểm của AB và CD.

Ta có $\vec{O A} + \vec{O B} = 2 \vec{O I}$ và $\vec{O C} + \vec{O D} = 2 \vec{O J}$ .

Mà $\vec{O I}, \vec{O J}$ là hai vectơ đối nhau.

Do đó $2 \vec{O I} \neq 2 \vec{O J}$ .

Suy ra $\vec{O A} + \vec{O B} \neq \vec{O C} + \vec{O D}$ ⇒ C sai.

Đáp án D: Ta có OI là đường trung bình của tam giác ABD.

Suy ra $\vec{O I} = \frac{1}{2} \vec{D A}$ .

Ta có $\vec{O A} + \vec{O B} = 2 \vec{O I} = 2. \frac{1}{2} \vec{D A} = \vec{D A}$ ⇒ D đúng.

Vậy ta chọn đáp án C.

Câu 6:

21/07/2024

Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$ .

A. M là trung điểm BC;

B. M là trung điểm IC;

C. M là trung điểm IA;

D. M là điểm trên cạnh IC sao cho IM = 2MC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} \Leftrightarrow 2 \vec{M I} + 2 \vec{M C} = \vec{0} \Leftrightarrow 2 (\vec{M I} + \vec{M C}) = \vec{0} \Leftrightarrow \vec{M I} + \vec{M C} = \vec{0}$ .

Do đó ta suy ra M là trung điểm IC.

Vậy ta chọn đáp án B.

Câu 7:

11/10/2024

Cho hình bình hành ABCD, điểm M thỏa mãn $4 \vec{A M} = \vec{A B} + \vec{A D} + \vec{A C}$ . Xác định vị trí điểm M.

A. M là trung điểm AC;

B. Điểm M trùng với điểm C;

C. M là trung điểm AB;

D. M là trung điểm AD.

Xem đáp án

Đáp án đúng là: A

* Phương pháp giải:

- Dùng định nghĩa tổng của hai vectơ, quy tắc ba điểm về tổng, quy tắc hình bình hành và các tính chất của tổng các vectơ.

* Lời giải:

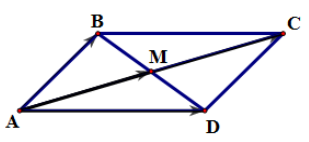
Theo quy tắc hình bình hành, ta có $\vec{A B} + \vec{A D} = \vec{A C}$ .

Ta có $4 \vec{A M} = \vec{A B} + \vec{A D} + \vec{A C}$

$\Leftrightarrow 4 \vec{A M} = 2 \vec{A C}$

$\Leftrightarrow \vec{A M} = \frac{1}{2} \vec{A C}$

Suy ra M là trung điểm AC.

* Một số lý thuyết và dạng bài tập về tổng hai vectơ:

a) Lý thuyết:

Quy tắc hình bình hành

Nếu OACB là hình bình hành thì ta có $\vec{O A} + \vec{O B} = \vec{O C}$ .

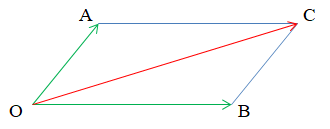
b) Dạng bài tập

- Tính tổng hai vectơ

- Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vectơ.

Xem thêm các bài viết liên quan hay, chi tiết:

Tổng và hiệu của hai vectơ và cách giải bài tập (2024) chi tiết nhất

80 câu trắc nghiệm Vectơ cơ bản

Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10

Câu 8:

21/07/2024

Cho tam giác đều ABC cạnh a. Tính độ dài $\vec{A B} + \vec{A C}$ .

A. $|\vec{A B} + \vec{A C}| = a \sqrt{3}$

B. $|\vec{A B} + \vec{A C}| = \frac{a \sqrt{3}}{2}$

C. $|\vec{A B} + \vec{A C}| = 2 a$

D. Đáp án khác

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

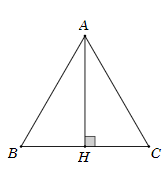
Gọi H là trung điểm BC. Ta suy ra BH = $\frac{B C}{2} = \frac{a}{2}$ .

Vì H là trung điểm BC nên ta có $\vec{A B} + \vec{A C} = 2 \vec{A H}$ .

Do đó $|\vec{A B} + \vec{A C}| = |2 \vec{A H}| = 2 A H$ .

Tam giác ABC đều có AH là đường trung tuyến.

Suy ra AH cũng là đường cao của tam giác ABC.

Tam giác ABH vuông tại H: $A H^{2} = A B^{2} - B H^{2}$ (Định lý Pytago)

$\Leftrightarrow A H^{2} = a^{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4}$

$\Rightarrow A H = \frac{a \sqrt{3}}{2}$ .

Suy ra $|\vec{A B} + \vec{A C}| = 2 A H = 2. \frac{a \sqrt{3}}{2} = a \sqrt{3}$ .

Vậy ta chọn đáp án A.

Câu 9:

10/11/2024

Cho tam giác ABC có điểm O thỏa mãn $|\vec{O A} + \vec{O B} - 2 \vec{O C}| = |\vec{O A} - \vec{O B}|$ . Khẳng định nào sau đây là đúng?

A. Tam giác ABC đều;

B. Tam giác ABC cân tại C;

C. Tam giác ABC vuông tại C;

D. Tam giác ABC cân tại B.

Xem đáp án

Đáp án đúng là: C

Lời giải

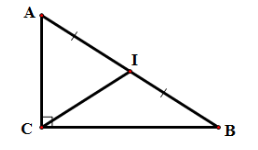
Gọi I là trung điểm AB. Ta suy ra $\vec{C A} + \vec{C B} = 2 \vec{C I}$ .

Ta có $|\vec{O A} + \vec{O B} - 2 \vec{O C}| = |\vec{O A} - \vec{O B}|$

$\Leftrightarrow |\vec{O A} - \vec{O C} + \vec{O B} - \vec{O C}| = |\vec{B A}|$

$\Leftrightarrow |\vec{C A} + \vec{C B}| = B A$

$\Leftrightarrow |2 \vec{C I}| = A B$

⇔ 2.CI = AB

$\Leftrightarrow C I = \frac{1}{2} A B$

Do đó tam giác ABC vuông tại C (đường trung tuyến trong tam giác vuông bằng một nửa cạnh huyền).

*Phương pháp giải :

Chứng minh bằng cách dùng tính chất của cạnh huyền trong tam giác vuông

*Lý thuyết:

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng $\frac{1}{2}$ cạnh huyền.

Một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.

Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.

Xem thêm

Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông - Toán 9 Chân trời sáng tạo

TOP 40 câu Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án 2024) – Toán 9

Câu 10:

23/07/2024

Cho tam giác ABC và một điểm M tùy ý. Cho $\vec{v} = \vec{M A} + \vec{M B} - 2 \vec{M C}$ . Hãy xác định vị trí của điểm D sao cho $\vec{C D} = \vec{v}$ .

A. D là điểm thứ tư của hình bình hành ABCD;

B. D là điểm thứ tư của hình bình hành ACBD;

C. D là trọng tâm của tam giác ABC;

D. D là trực tâm của tam giác ABC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có $\vec{v} = \vec{M A} + \vec{M B} - 2 \vec{M C} = \vec{M A} - \vec{M C} + \vec{M B} - \vec{M C} = \vec{C A} + \vec{C B} = 2 \vec{C I}$ (với I là trung điểm AB).

Do đó $\vec{v}$ không phụ thuộc vào vị trí của điểm M.

Khi đó $\vec{C D} = \vec{v} = 2 \vec{C I}$ .

Suy ra I là trung điểm CD.

Vậy D là điểm thứ tư của hình bình hành ACBD.

Vậy ta chọn đáp án B.

Câu 11:

21/07/2024

Cho tam giác ABC. Gọi M là trung điểm BC và N là trung điểm AM. Đường thẳng BN cắt AC tại P. Khi đó $\vec{A C} = x \vec{C P}$ thì giá trị của x là:

A. $- \frac{4}{3}$

B. $- \frac{2}{3}$

C. $- \frac{3}{2}$

D. $- \frac{5}{3}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

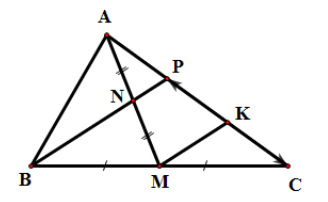
Kẻ MK // BP (K ∈ AC). Do M là trung điểm BC nên ta suy ra K là trung điểm CP (1).

Vì MK // NP, mà N là trung điểm AM nên ta suy ra P là trung điểm AK (2).

Từ (1), (2) ta suy ra AP = PK = KC.

Do đó AP = $\frac{1}{2}$ CP.

Ta có AC = AP + CP.

Suy ra AC = $\frac{3}{2}$ CP.

Vì $\vec{A C}, \vec{C P}$ ngược hướng với nhau.

Nên $\vec{A C} = - \frac{3}{2} \vec{C P}$ .

Do đó x = $- \frac{3}{2}$ .

Vậy ta chọn đáp án C.

Câu 12:

21/07/2024

Cho tam giác OAB vuông cân tại O với OA = OB = a. Độ dài của $\vec{u} = \frac{21}{4} \vec{O A} - \frac{5}{2} \vec{O B}$ là:

A. $\frac{a \sqrt{140}}{4}$

B. $\frac{a \sqrt{321}}{4}$

C. $\frac{a \sqrt{520}}{4}$

D. $\frac{a \sqrt{541}}{4}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

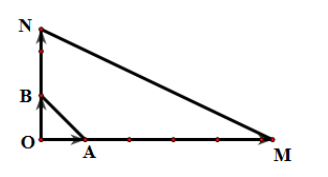
Dựng điểm M, N sao cho $\vec{O M} = \frac{21}{4} \vec{O A}$ và $\vec{O N} = \frac{5}{2} \vec{O B}$ . Khi đó ta có:

$|\vec{u}| = |\frac{21}{4} \vec{O A} - \frac{5}{2} \vec{O B}| = |\vec{O M} - \vec{O N}| = |\vec{N M}| = M N$ .

Từ dữ kiện $\vec{O M} = \frac{21}{4} \vec{O A}$ .

Ta suy ra $\vec{O M}$ cùng phương với $\vec{O A}$ .

Vì $\vec{O M}, \vec{O A}$ có cùng điểm đầu là O.

Nên giá của $\vec{O M}, \vec{O A}$ trùng nhau.

Do đó ta có OM ≡ OA.

Tương tự ta có ON ≡ OB.

Mà OA ⊥ OB (tam giác OAB vuông cân tại O).

Do đó OM ⊥ ON.

Ta có $\vec{O M} = \frac{21}{4} \vec{O A} \Leftrightarrow |\vec{O M}| = |\frac{21}{4} \vec{O A}| \Leftrightarrow O M = \frac{21}{4} O A = \frac{21 a}{4}$ .

Tương tự, ta có $\vec{O N} = \frac{5}{2} \vec{O B} \Leftrightarrow |\vec{O N}| = |\frac{5}{2} \vec{O B}| \Leftrightarrow O N = \frac{5}{2} O B = \frac{5 a}{2}$ .

Tam giác OMN vuông tại O: $M N^{2} = O M^{2} + O N^{2}$ (Định lý Pytago)

\Leftrightarrow M N^{2} = \frac{441 a^{2}}{16} + \frac{25 a^{2}}{4} = \frac{541 a^{2}}{16}

$\Rightarrow M N = \frac{a \sqrt{541}}{4}$ .

Vậy ta chọn đáp án D.

Câu 13:

23/07/2024

Cho tam giác ABC có trọng tâm G. Biểu diễn $\vec{A G}$ theo hai vectơ $\vec{A B}, \vec{A C}$ .

A. $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C})$

B. $\vec{A G} = \frac{1}{6} (\vec{A B} + \vec{A C})$

C. $\vec{A G} = \frac{1}{6} (\vec{A B} - \vec{A C})$

D. $\vec{A G} = \frac{1}{3} (\vec{A B} - \vec{A C})$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

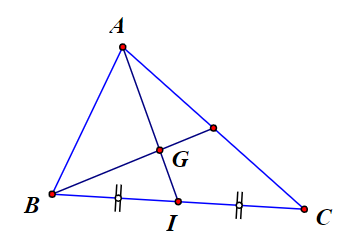
Gọi I là trung điểm BC. Ta suy ra $2 \vec{A I} = \vec{A B} + \vec{A C}$

Ta có G là trọng tâm tam giác ABC nên $A G = \frac{2}{3} A I$ .

Mà $\vec{A G}, \vec{A I}$ cùng hướng.

Do đó $\vec{A G} = \frac{2}{3} \vec{A I}$ .

Suy ra $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C})$ .

Vậy ta chọn đáp án A.

Câu 14:

21/07/2024

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm AB, CD. Khi đó $\vec{A C} + \vec{B D}$ bằng

A. $\vec{M N}$

B. $2 \vec{M N}$

C. $3 \vec{M N}$

D. $- 2 \vec{M N}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

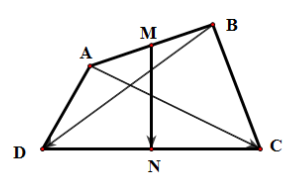
Vì M là trung điểm AB nên $\vec{M A} + \vec{M B} = \vec{0} \Leftrightarrow - (\vec{A M} + \vec{B M}) = \vec{0} \Leftrightarrow \vec{A M} + \vec{B M} = \vec{0}$ .

Vì N là trung điểm CD nên $\vec{N C} + \vec{N D} = \vec{0}$ .

Theo quy tắc ba điểm, ta có $\vec{A C} + \vec{B D} = \vec{A M} + \vec{M N} + \vec{N C} + \vec{B M} + \vec{M N} + \vec{N D}$

Suy ra $\vec{A C} + \vec{B D} = (\vec{A M} + \vec{B M}) + (\vec{N C} + \vec{N D}) + 2 \vec{M N} = \vec{0} + \vec{0} + 2 \vec{M N} = 2 \vec{M N}$

Vậy ta chọn đáp án B.

Câu 15:

22/07/2024

Cho hình bình hành ABCD tâm O và điểm M bất kỳ. Khẳng định nào sau đây đúng?

A. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M O}$

B. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 2 \vec{M O}$

C. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 3 \vec{M O}$

D. $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

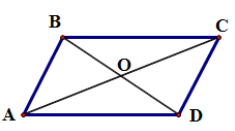
Vì O là tâm của hình bình hành ABCD nên O là trung điểm của AC và BD.

Vì O là trung điểm AC và M là điểm tùy ý nên $\vec{M A} + \vec{M C} = 2 \vec{M O}$ (1).

Vì O là trung điểm BD và M là điểm tùy ý nên $\vec{M B} + \vec{M D} = 2 \vec{M O}$ (2).

Lấy (1) + (2) vế theo vế, ta được: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

Vậy ta chọn đáp án D.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3